01_Физические_основы_механики

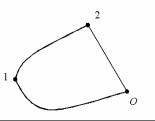
Работа, совершаемая консервативными силами поля над частицей, при переходе частицы из некоторой точки в нулевое поло-

жение, называется потенциальной энергией частицы в этой

точке в поле консервативных сил

U (x, y, z) = A(x, y, z),(x0, , y0 , z0 ) , Дж.

Очевидно, что значение U (x, y, z) зависит от выбора нулевого положения – точки О. Пусть частица из некоторой точки 1 переходит в нулевое положение О двумя путями: по пути 1-О и по пути 1-2-О, где 2 – некоторая точка. При этом частица находится в поле консервативных сил. Если силы, действующие на частицу, консервативные, то

A10 = A12 + A20 .

Из определения потенциальной энергии

A10 =U1, A20 =U2 .

Здесь U1,U2 – потенциальная энергия частицы в 1-й и 2-й точках. Далее запишем

U1 = A12 +U 2 , A12 =U1 −U 2 .

Рис. 4.10. Перемещение материальной точки в поле консервативных сил

Работа консервативной силы при перемещении частицы из произвольного начального положения 1 в произвольное конечное положение 2 по произвольному пути равна разности потенциальной энергии частицы в начальном и конечном положениях или убыли потенциальной энергии частицы

A12 = U1 −U2 .

Если частица совершает элементарное перемещение, то dA = −dU .

80

4.7. Вычисление потенциальной энергии

Потенциальная энергия частицы в однородном поле силы тяжести

Работа, совершаемая однородной силой тяжести над частицей массой m равна

A12 = mgz1 − mgz2 .

Видно, что работа не зависит от пути перемещения. Кроме того, если путь замкнутый, то z1 = z2 , A12 = 0 . Таким образом, мож-

но сделать вывод о том, что однородная сила тяжести является консервативной силой. Пусть частица находится в точке 1 с ко-

ординатой z1 = h . Пусть нулевое положение О находится на поверхности Земли, так что z2 = 0 . По определению

U1 = A10 = mgh .

Потенциальная энергия материальной точки массой m, находящейся на высоте h в однородном поле тяжести Земли равна

U (h) = mgh .

Рассмотрим тело массой m. Разобьем тело на элементарные массы mi – материальные точки. Обозначим zi – вертикальная

координата i-ой материальной точки, отсчитанная от некоторой точки О.

Потенциальной энергией системы материальных точек в

поле консервативных сил называется величина, равная алгебраической сумме потенциальных энергий материальных точек системы в данном поле консервативных сил

		N
		U = ∑Ui .
Запишем		i
N	N	N		1	N
U = ∑Ui = ∑mi gzi = g∑mi zi = gM					∑mi zi .
i =1	i =1	i=1		M i =1

N

ЗдесьM = ∑mi .

i =1

81

Центр масс системы определяется выражениями

r	1			N	r		1			N
RC =				∑mi ri		, xC =				∑mi xi ,
		M i=1					M i=1
	1			N			1			N
yC =				∑mi yi , zC =						∑mi zi .
	M i=1							M i=1

Следовательно, потенциальная энергия тела равна

U = MgzC .

Здесь zC – вертикальная координата центра масс системы.

Потенциальная энергия системы частиц в однородном поле силы тяжести равнапроизведению массы системы наускорение свободного паденияинавертикальнуюкоординатуцентрамасссистемы.

Потенциальная энергия деформированной пружины

Работа, совершаемая упругой силой равна

A =	kx	2	−	kx	2
	1			2		.
12	2			2

Работа определяется только начальным x1 и конечным x2 положениями свободного конца пружины и не зависит от «пути перехода» из 1 в 2, следовательно, упругая сила есть консервативная сила. Пусть состояние 2 определяется условием x2 = 0 . В этом состоянии пружина не имеет деформации. Будем считать такое состояние нулевым положением.

Обозначим деформацию пружины x , x1 = x . Тогда потенциальная энергия деформированной пружины равна

U = A =	kx	2	.
10	2

Потенциальная энергия гравитационного поля

Пусть частица m находится в гравитационном поле, создаваемом другой частицей М. При элементарном перемещении частицы m силы поля совершает работу dA, равную убыли потенциальной энергии частицы в этом поле

82

dA = −dU .

dA = Fdrr = −γ mMr 2 rr drr = −γ mMr 2 rdrr = −γ mMr 2 dr = −dU . dU =γ mMr 2 dr, U = ∫γ mMr 2 dr = −γ mMr +C.

Пусть выполняется условие r = ∞,U = 0 . Такое выражение

называется условием нормировки потенциальной энергии. За-

пишем

0 = 0 +C,C = 0 . U (r) = −γ mMr .

4.8. Потенциальная энергия и консервативная сила

Пусть частица, на которую действует консервативная сила F , совершает элементарное перемещение dr . Элементарная работа

силы равна

dA = Fdrr = (Fx i + Fy j + Fz k )(dxi + dyj + dzk )=

= Fx dx + Fy dy + Fz dz = −dU.

Пусть частица перемещается так, что выполняются условия: y = const, z = const, dy = 0, dz = 0 .

	Тогда
	Fx dx = −dU , Fx = −	dU			y=const , Fx = −	∂U	.
		dx
					z=const	∂x

Выражение ∂U называется частной производной функции

∂x

U(x, y, z) по переменной x , при этом y = const, z = const . Аналогично можно получить для проекций Fy и Fz :

Fy	= −	∂U		, Fz = −	∂U	.
		∂y
Умножим Fx , Fy , Fz				r∂z
	на орты i , j, k и сложим:
			83

r

r

r

∂U

r

∂U

r

∂U

r

i

+

j

+

Fx i + Fy j + Fz k = −

∂x

∂y

∂z

k ,

r

∂U

r

∂U

r

∂U

r

i

+

j

+

F = −

∂x

∂y

∂z

k .

Величину в скобках называют градиентом скалярной функции U и обозначают так: gradU . Полученное выражение для

градиента справедливо в декартовой системе координат.

Сила, действующая со стороны консервативного поля на частицу в некоторой точке поля, равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля.

4.9. Кинетическая энергия частицы

Запишем для частицы второй закон Ньютона m ddtV = Fr .

За время dt частица совершает перемещение

Vdt = drr.

Умножим выражения друг на друга

m ddtV Vrdt = Frdrr, mdVrdV = Fdrr.

Запишем

V 2 =V 2 .

Вычислим дифференциал от обеих частей

2VdV = 2VdV , VdV =VdV , mVdV = Fdrr.

Запишем для левой части последнего равенства

mVdV = d mV 2 .2

Далее

d mV 2 = Frdrr.2

84

В левой части имеем приращение некоторой функции, которая называется кинетической энергией частицы

T = mV2 2 , Дж.

По определению T ≥0.

В правой части уравнения – элементарная работа силы

Fdrr = dA .

Итак , dT = dA.

Элементарная работа силы, действующей на частицу, равна элементарному приращению кинетической энергии частицы

dT = dA.

Конечное перемещение частицы 1-2 можно представить как сумму бесконечно малых перемещений, на каждом из которых

dTi = dAi .

Просуммируем выражения по всем N перемещениям

N N

∑dTi = ∑dAi .

i=1 i=1

При N →∞получим

∫2 dT = ∫2 dA .

1 1

Интеграл слева равен

∫2 dT =T2 −T1 .

1

Интеграл справа в общем случае зависит от формы пути, поэтому

∫2 dA = A12 . 1

В итоге T2 −T1 = A12 .

Работа силы, действующей на частицу на некотором перемещении, равна приращению кинетической энергии частицы на этом перемещении

A12 =T2 −T1 .

85

4.10. Полная механическая энергия частицы

Пусть частица находится в некотором поле консервативных сил. Обозначим силу, действующую на нее со стороны этого поля

F конс . Пусть также на частицу действуют силы, не принадлежащие указанному силовому полю. Силы, не принадлежащие рассматриваемому в данной задаче полю консервативных сил, назы-

ваются сторонними силами F стор . Сторонние силы могут быть как консервативными, так и не консервативными. Таким образом,

в общем случае, силаF , действующая на частицу, равна

			F = F конс		+ F стор .
	Рассмотрим перемещение частицы из точки 1 в точку 2. Вы-
	числим работу
		2		2
	A12	= ∫Fdrv r		= ∫(Frконс + Frстор )drr =
		1		1		.
	2 r	r	2	r	r
	= ∫F консdr		+ ∫F сторdr = A12 конс + A12			стор

11

Сдругой стороны,

A12 =T2 −T1 , T2 −T1 = A12 конс + A12 стор.

Кроме того,

A12 конс =U1 −U 2 ,T2 −T1 =U1 −U 2 + A12 стор ,

(T2 +U 2 )−(T1 +U1 )= A12 стор.

Сумма кинетической энергии частицы и ее потенциальной энергии называется полной механической энергией частицы

E =T +U ,Дж.

Следовательно,

E2 − E1 = A12 стор .

86

Приращение полной механической энергии частицы на некотором перемещении равно работе сторонних сил, действующих на частицу на этом перемещении

E2 − E1 = A12 стор .

В случае элементарного перемещения

dE = dT .

4.11.Закон сохранения полной механической энергии частицы

Пусть на частицу действуют только консервативные силы

F конс ≠ 0, F стор = 0,	dAстор = 0, A стор = 0.
	12
Можем записать
E2 − E1 = 0, E2	= E1 = E = const.

Если на частицу действуют только консервативные силы, то полная механическая энергия частицы остается постоянной или сохраняется

E =T +U = const.

4.12.Закон сохранения полной механической энергии системы частиц

Для системы N частиц можно получить выражение

N

E= T +U ,T = ∑Ti

i=1

N

,U = ∑Ui .

i=1

Здесь T, U – кинетическая и потенциальная энергия систе-

мы частиц.

Полная механическая энергия системы частиц, на которые действуют только консервативные силы остается постоянной, т.е. сохраняется

E =T +U = const.

87

4.13. Соударение двух тел

Соударением (столкновением) тел называется такое взаимо-

действие при котором время взаимодействия мало, а силы взаимодействия велики. При этом систему тел, участвующих в соударении можно считать замкнутой.

Абсолютно упругий удар

Абсолютно упругим ударом называется столкновение, при котором кинетическая энергия системы не изменяется. Рассмотрим удар двух однородных шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, соединяющей

их центры. Обозначим массы шаров m1 , m2 , скорости шаров до удара V1,V2 , а скорости после удара соответственно u1 ,u2 .

Рис. 4.11. Упругий удар двух тел

Запишем законы сохранения импульса и энергии

									2		2				r 2		r 2
m Vr		+ m Vr		= m ur		+ m	ur	2	,	m1V1	+	m2V2		=	m1u1	+	m2u2	.
1	1	2	2	1	1	2			2		2		2				2
Преобразуем второе уравнение
				m (V 2 −ur 2 ) = m (ur 2 −V									2 ),
		m1 (Vr1 −ur11 )1(Vr1 +u1r1 )= m22									(ur22 −Vr2 )2 (ur2 +Vr2 ).

Из первого уравнения получим

m1 (V1 −ur1 )= m2 (ur2 −V2 ).

88

Из соображения симметрии следует, что скорости шаров u1,u2 будут направлены вдоль прямой, соединяющей центры ша-

ров, следовательно,			r	r			r
								.
		V + u		=u	2	+V
	1		1			2
Окончательно можно получить результат
ur	=	2m2V2 + (m1 − m2 )V1		,ur	=		2m1V1 + (m2 − m1 )V2		.
1		m1 + m2		2				m1 + m2

Для численных расчетов нужно спроецировать выражения на ось x , вдоль которой движутся шары.

Рассмотрим нормальное соударение шара с неподвижной массивной стенкой. Рассматриваем стенку как шар бесконечно большого радиуса и массы.

Запишем

	r				r
			m1
	2V2 +				−1 V1			m1
ur =		m2				= −Vr,	Vr = 0,		<<1 ≈ 0.
	m							m2
1						1	2
		1
				+1
	m2

Рис. 4.12. Упругий удар тела о стенку

89