2.5. Модели сигналов на основе рядов Фурье. Интеграл Фурье

2.5.1. Модели сигналов на основе действительного ряда Фурье

Рассмотрим построение моделей сигналов на основе действительного ряда Фурье.

Пусть наблюдения cигнала заданы в виде действительной функции на конечном интервале времениРассмотрим варианты условий сходимости рядов Фурье для^. Первый вариант: если в некотором промежутке с центром в точкефункцияимеет ограниченное изменение, то её ряд Фурье в указанном интервале длясходится кВторой вариант: если функцияопределённая на интервалеимеет на нём не более чем конечное число точек разрыва, её ряд Фурье в точке непрерывностисходится кили к суммев каждой точке разрываБудем полагать, что для рассматриваемого сигналавыполнены сформулированные условия сходимости.

Выбирается модель для указанного сигнала в форме действительного ряда Фурье следующего вида

(2.5.1)

Значения модельных частот фиксированы и определяются длиной интервала наблюдения, модельные синусоиды располагаются с шагом по частотекоторый зависит отВектор параметров модели имеет бесконечную размерность,Благодаря выбору частотного параметраоказывается, что на интервале времениукладывает целое число периодов базисных функцийиВследствие этого, указанные базисные функции являются ортогональными.

Функционал для решения задачи аппроксимации функции наблюдений на основе сформированной модели имеет вид

Нахождение вектора параметров модели сводится к минимизации указанного функционала, который, очевидно, является квадратичным по с:

,

Ограничимся конечным числом синусоид, составляющих модель, равным L. В этом случае вектор базисных функций для модели (2.5.1) имеет размерность и выглядит на интервале следующим образом:

Нетрудно убедиться в том, что для составляющие базис функции ортогональны. Действительно, легко проверить, что интегралы от произведений базисных функций равняются нулю:

,

и

Вычислим интегралы от квадратов базисных функций:

Основываясь на произведённых выкладках, с учётом формулы (2.4.14) для решения линейной системы с ортогональными базисными функциями, получим оптимальные значения коэффициентов модели для фиксированного L:

Устремим число базисных функций в бесконечность, Естественно, можно сразу записать, опустив знакформулы для оптимальных параметров модели, которые являются известными коэффициентами разложения Фурье:

.

В силу ортогональности базисных функций модели ряда Фурье мощность P сигнала, сформированного на основе ряда Фурье, слагается из мощностей составляющих синусоид мощность дляl‑й синусоиды определяется амплитудами

.

Благодаря ортогональности данного базиса для рассматриваемой модели возможно представление дискретного спектра мощности в виде бесконечной последовательности равноотстоящих на по оси частот значений

Сходимость функций модельного ряда Фурье зависит от числа членов, которые учитываются в разложении и от свойств аппроксимируемого сигнала. В случае, если производные для сигнала претерпевают разрывы или резкие изменения, то модельный ряд Фурье становится колебательным в области разрывов (резких изменений) и возникает так называемый эффект Гиббса.

Рассмотрим численные примеры вычисления модельных рядов Фурье с конечным числом членов, основываясь на (2.5.1):

Пример 1. Содержит разложение в ряд Фурье на интервале времени для ступенчатого сигнала

длядля (2.5.2)

Коэффициенты Фурье для ряда Фурье вычисляются по следующим формулам, исходя из вида аппроксимируемой функции

Проинтегрируем, опустим промежуточные выкладки, получим

На рис. 2.5.1а изображён график функции модельного ряда Фурье для и– кривая1, в точках разрыва ряд Фурье стремится к значению 1/2. Пунктирной линией 2 изображён аппроксимируемый сигнал Видно, что функция претерпевает довольно значительные колебания в областях нарушения непрерывности (в окрестности точеки т.е. имеет место эффект Гиббса.

Пример 2. Содержит разложение в ряд Фурье на интервале времени длительностью для кусочно-линейного непрерывного сигнала

для для для для

(2.5.3)

Уменьшение колебаний из-за эффекта Гиббса может быть достигнуто при условии, если аппроксимируемый сигнал будет непрерывным.

Непрерывность обеспечивается при условии выполнения равенств

Для нахождения коэффициентов Фурье запишем интегралы

, , , ,, ,

(2.5.4)

.

Вычисления (2.5.4) произведены с помощью табличных интегралов

На рис. 2.5.1б изображён график функции модельного ряда Фурье Для приняты значенияиКолебания функции модельного ряда уменьшились, эффект Гиббса почти устранён.

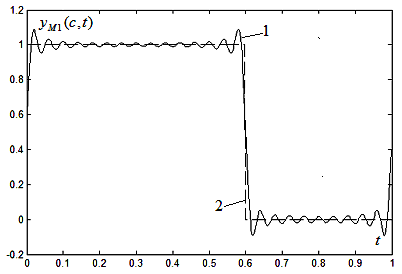
Рис. 2.5.1а. Функция модельного ряда Фурье для ступенчатого сигнала

Рис. 2.5.1б. Функция модельного ряда Фурье для кусочно-линейного

непрерывного сигнала

2. Модели сигналов на основе комплексного ряда Фурье

Для многих задач ЦОС используется обобщение разложения Фурье на комплексный случай. Пусть произведено наблюдение комплексной функции на интервалемодель сигнала представится комплексным рядом Фурье

(2.5.5)

Комплексный вектор параметров модели имеет бесконечную размерность Функционал остаточной суммы примет вид

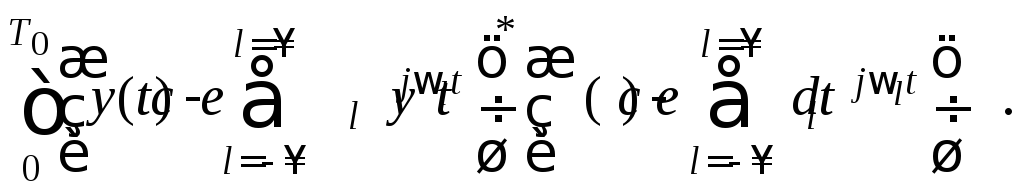(2.5.6)

Так же как и для разд. 2.5.1, ограничимся конечным числом комплексных модельных синусоид, которые составляют модель; пусть число модельных синусоид равняется L. В этом случае вектор базисных функций для модели (2.5.5) имеет размерность и выглядит следующим образом

Нетрудно убедиться в том, что на интервале времени составляющие базис функции ортогональны. Действительно, интегралы от произведений базисных функций для равняются нулю; нетрудно видеть, что с учётом комплексности выполняется равенство:

Для справедливо соотношение

Оптимальные параметры модели обеспечивающие минимум функционала (2.5.6), после того как сделаны необходимые выкладки и предельный переходопределяются следующими интегралами (опущен знак):

(2.5.7)

Пусть для рассматриваемой функции сигнала выполняются сформулированные в разд. 2.5.1 условия сходимости с учётом комплексности. Тогда на оптимальныхиз (2.5.7), очевидно, должно выполняться равенство

(2.5.8)

Вследствие (2.5.8) остаточная сумма квадратов (2.5.6) – значение функционала для оптимальных параметров – должно принимать нулевое значение . Таким образом, можно записать два взаимных равенства:

Для действительных сигналов можно выяснить соотношения между коэффициентами действительногои комплексногорядов Фурье. Действительно, можно записать

.

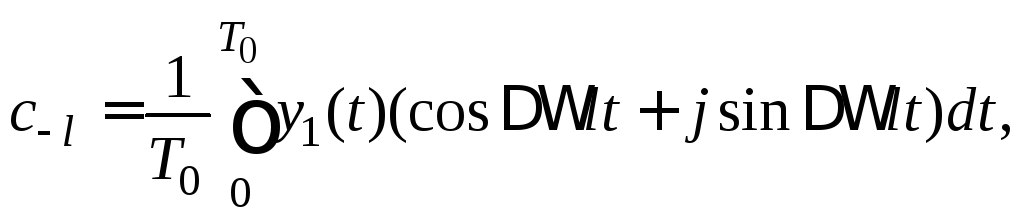
Тогда легко видеть, что справедливы следующие равенства для и

и

Мощность l-й комплексной модельной синусоидальной функции вычисляется интегрированием на интервале

Благодаря ортогональности используемого комплексного базиса общая мощность сигнала представляется в виде суммы мощностей составляющих как для положительных, так и отрицательных частот.

2.5.3. Интеграл Фурье. Свойства интеграла Фурье

Интеграл Фурье реализуется на основе рассмотрения комплексного ряда Фурье для бесконечного временного интервала; будем полагать, что сигнал с конечным числом точек разрывов определён дляи для него выполняется условие абсолютной интегрируемости

Данные условия являются достаточными для существования преобразования Фурье сигнала

Без потери общности примем временной интервал симметричным пусть этот интервал расширяется

Запишем коэффициенты разложения комплексного ряда Фурье для расширяющегося временного интервала

Подставим выражение в:

.

Устремим обозначимполучим в пределе

Сформируем интегралы

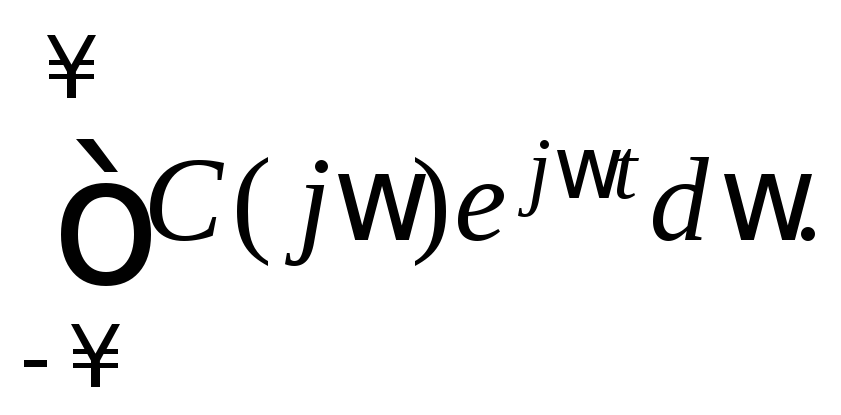
Функцию называютинтегралом Фурье, или преобразованием Фурье для Два последних интеграла являются прямым и обратным преобразованием Фурье. Сигнал представляется как во временной области при традиционном анализе, так и в частотной области в виде непрерывных коэффициентов разложений Фурье

Физический смысл функции очевиден. Преобразование Фурьепредставляет собой предельную функцию коэффициентов комплексного ряда Фурье.

Функция в общем случае является комплексной функцией частоты и допускает следующие представления:

где и– действительные и мнимые части; – модуль и фаза преобразования Фурье.

Разберём некоторые свойства преобразований Фурье.

1. Из определения преобразования Фурье следует его линейность или свойство суперпозиции. Пусть функция представляет собой взвешенную сумму функцийдля которых заданы их преобразования Фурье

Тогда, очевидно, преобразование Фурье длявычисляется как взвешенная сумма преобразований Фурье:

2. Пусть  – масштабирующий множитель, преобразующий функцию виВычислим преобразование Фурье дляОпределими:

Введём переменную сделаем подстановку ви выразимчерез:

3. Пусть задано преобразование Фурье для функции Введём запаздывание (сдвиг по времени) для функции сформируемВычислим преобразование Фурье для:

откуда вытекает

Сделав аналогичные выкладки, получим, что преобразование Фурье для функции умноженной насдвигается по частоте

4. Вычисление преобразование Фурье для комплексной синусои­ды требует предварительного определения-функ­ции.

Импульсной -функцией называется такая функция, которая удовлетворяет следующим двум условиям:

1) дляидля

2) для любого

Импульсная -функция может рассматриваться как предел обычной функции приНапример,

для идля

Для -функции устанавливается важное равенство:

если непрерывна в точкеиДанное свойство может быть доказано путём вычисления следующего предела:

С учётом сделанного определения можно записать преобразование Фурье для

Действительно, подставив в выражение для обратного преобразования Фурье, получим тождество

5. Пусть – преобразование Фурье для функцииНайдём выражение для преобразования Фурье для производнойЗапишем выражение для обратного преобразования Фурье и продифференцируем его:

Из последнего выражения следует, что

Сделав почти аналогичные выкладки, можно записать преобразование Фурье для интеграла от которое будет иметь вид

6. Вычислим преобразование Фурье для симметричного единичного импульса:

,

Ввиду симметричности рассматриваемого единичного импульса его преобразование Фурье является действительной функцией.

7. Найдём преобразование Фурье для произведения функций – соответственно, преобразования Фурье дляЗапишем интегралы

Изменив порядок интегрирования, с учётом выражения интеграла Фурье для комплексной синусоиды получим

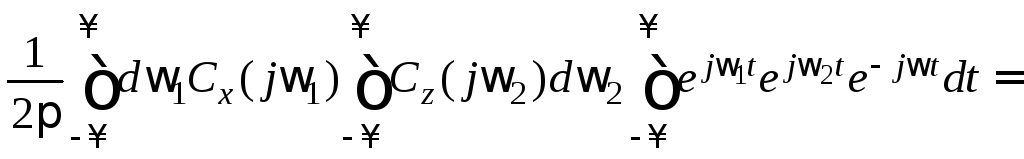
Преобразование Фурье от произведения функций равняется свёртке преобразований Фурье сомножителей.