
- •Глава 5. Определенный интеграл
- •5.1. Задачи, приводящие к понятию определенного интеграла
- •5.2. Интегральные суммы, их свойства
- •Определение определенного интеграла
- •5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона - Лейбница
- •5.4. Свойства определенного интеграла
- •5.5. Методы интегрирования определенных интегралов
- •5.6. Несобственные интегралы с бесконечными пределами интегрирования
- •5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования
- •5.8. Несобственные интегралы от разрывных функций, неограниченных в точках разрыва
- •5.9. Теоремы о сходимости несобственных интегралов от разрывных функций
- •5.10. Геометрические приложения определенных интегралов
- •5.10.1. Вычисление площадей фигур
- •5.10.2. Вычисление объемов тел вращения
- •5.10.3. Длина дуги кривой
- •5.11. Численные методы нахождения определенных интегралов
- •5.11.1. Формулы прямоугольников
- •5.11.2. Формула трапеций
- •5.11.3. Формула Симпсона для приближенного вычисления определенных интегралов
- •5.12. Производная интеграла, зависящего от параметра
- •Глава 6. Двойные интегралы
- •6.1. Определение двойного интеграла
- •6.2. Геометрический смысл двойного интеграла
- •6.3. Свойства двойных интегралов
- •6.4. Вычисление двойных интегралов
- •6.5. Двойные несобственные интегралы с бесконечными пределами интегрирования
5.11.1. Формулы прямоугольников
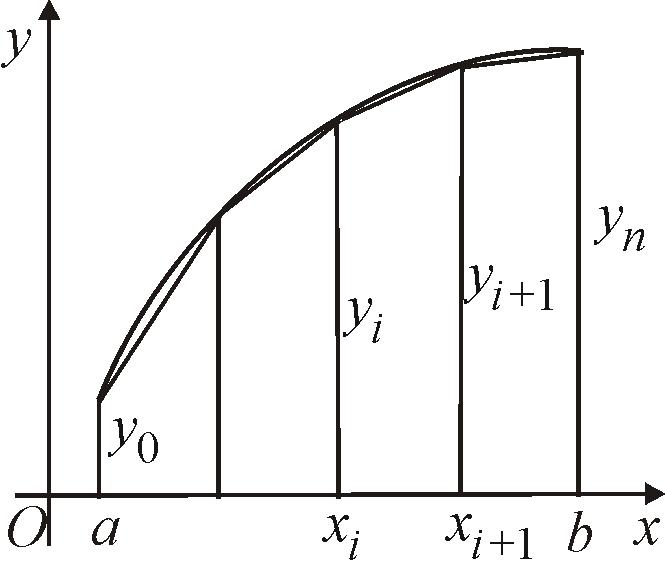
Наиболее простые формулы для приближенного вычисления интегралов получаются при замене подынтегральной функции прямой. Эти формулы называются формулами прямоугольников и трапеций.

Рис. 72
Заменяя значение
функции
![]() на элементарных отрезках постоянными
значениями (рис. 72), можно получить две
формулы в зависимости от того, равняются
ли на i-м
отрезке
на элементарных отрезках постоянными
значениями (рис. 72), можно получить две
формулы в зависимости от того, равняются
ли на i-м
отрезке
![]() эти постоянные
эти постоянные
![]() или
или
![]() .
В зависимости от этого площадь i-й
элементарной трапеции (прямоугольника)
равна либо
.
В зависимости от этого площадь i-й
элементарной трапеции (прямоугольника)
равна либо
![]() ,
либо
,
либо
![]() .
Суммируем площади получающихся
прямоугольников, получаем две формулы:
.
Суммируем площади получающихся
прямоугольников, получаем две формулы:
1.
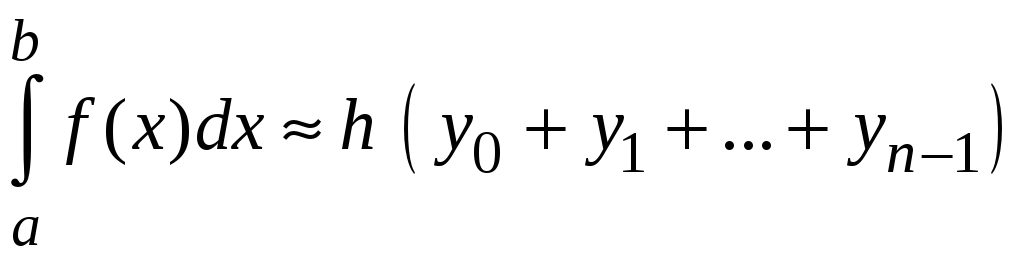 или
или
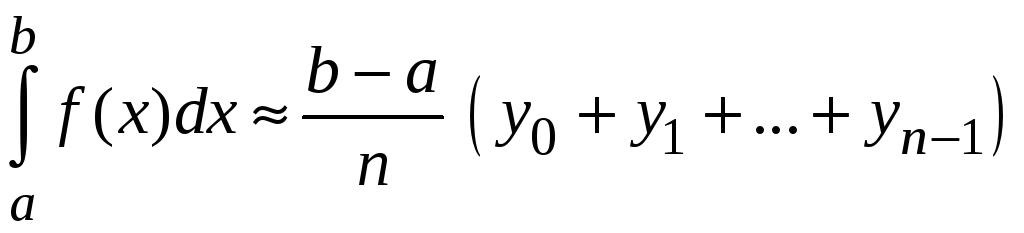 ;
;
2.
 или
или
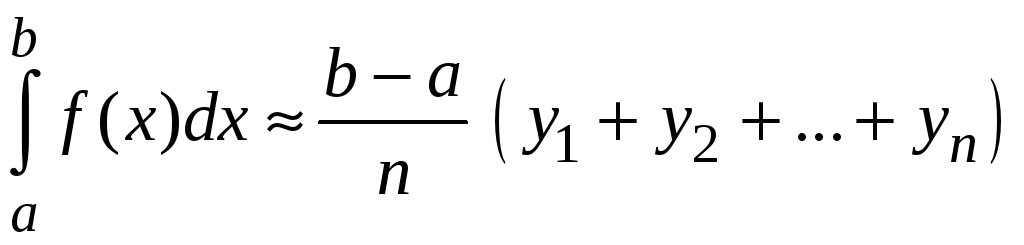 .
.
5.11.2. Формула трапеций
|
Рис. 73 |
Заменим на каждом
элементарном отрезке
Приближенное значение определенного интеграла найдем как сумму площадей элементарных трапеций |
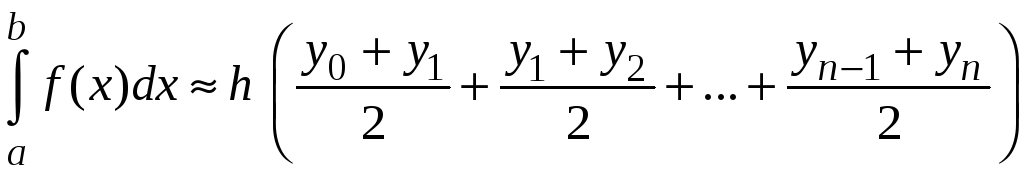 или
или
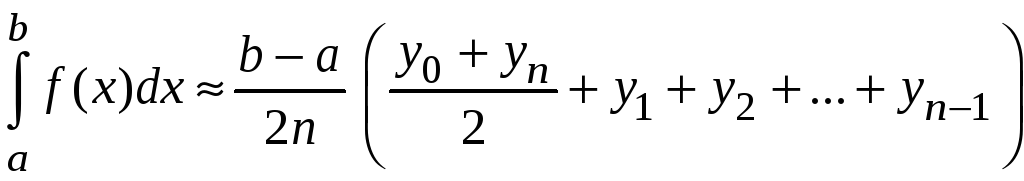
Вычисляемое по формуле трапеций значение интеграла равно среднему арифметическому значений этого интеграла, вычисленных по 1-ой и 2-ой формулам прямоугольников.
5.11.3. Формула Симпсона для приближенного вычисления определенных интегралов
Для получения формулы Симпсона интервал интегрирования разбивается на четное число 2n элементарных отрезков. На каждой паре отрезков подынтегральная функция заменяется параболой.
Теорема 5.
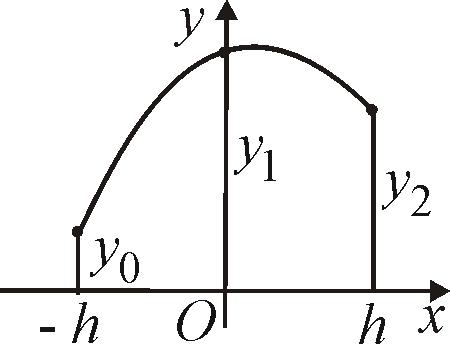
Площадь криволинейной трапеции,
ограниченной параболой
![]() на интервале длиной 2h
(рис. 74)
находится по формуле
на интервале длиной 2h
(рис. 74)
находится по формуле
![]() ,
где
,
где
![]() .
.
|
Рис. 74 |
Запишем уравнение
параболы, проходящей через точки
|
Уравнение параболы в рассматриваемом случае имеет вид
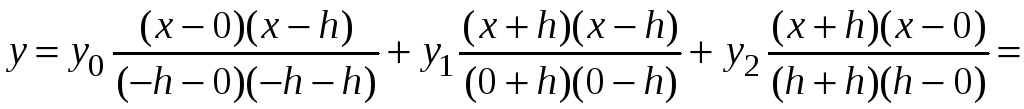
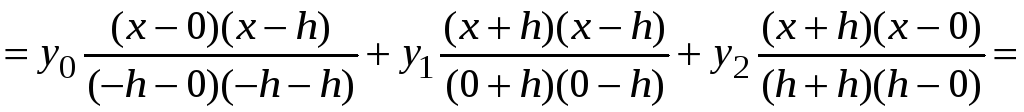
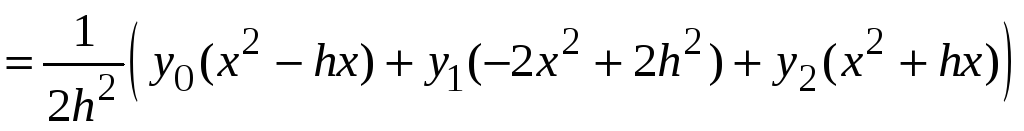 или
или
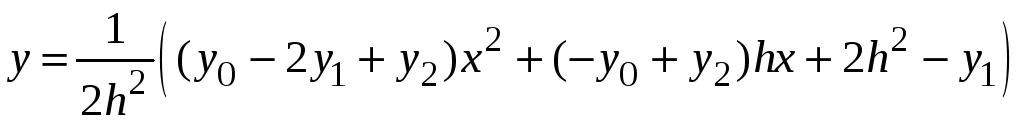 .
.
Найдем площадь
трапеции
![]() на отрезке
на отрезке
![]() как интеграл
как интеграл
 .
.
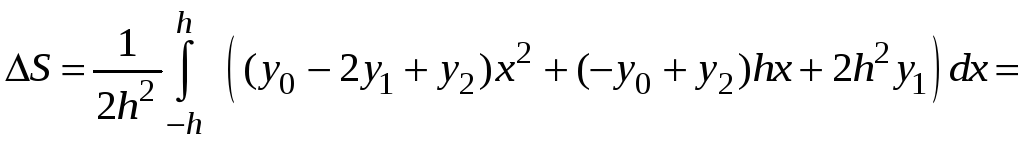
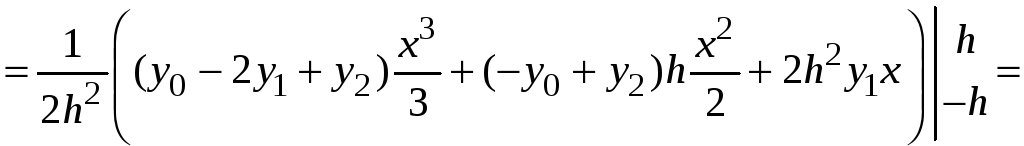
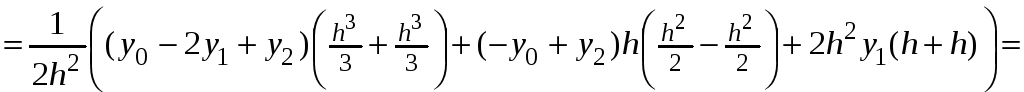
![]() .
.
Просуммируем площади трапеций на элементарных отрезках. Найдем приближенное значение интеграла
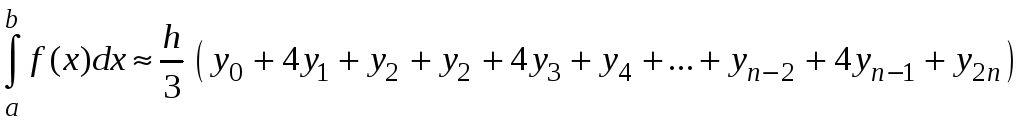 ,
,
где
![]() ,
приведем подобные и получим формулу
Симпсона в окончательном виде
,
приведем подобные и получим формулу
Симпсона в окончательном виде
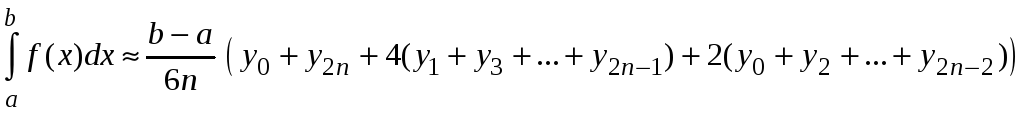 .
.
Для вычисления
определенного интеграла с заданной
точностью выбирают произвольно (на
основе опыта или интуитивно) число n
или 2n
элементарных
отрезков и по одной из формул для
приближенного вычисления производят
расчет интеграла. Получают некоторое
значение интеграла
![]() .
Затем увеличивают число элементарных
отрезков в 2 раза и снова производят
расчет. Получают новое значение интеграла
.
Затем увеличивают число элементарных
отрезков в 2 раза и снова производят
расчет. Получают новое значение интеграла
![]() .
Сравнивают полученные результаты. Если
.
Сравнивают полученные результаты. Если
![]() ,
где
- требуемая точность вычисления интеграла,
то расчет заканчивают. Значение
,
где
- требуемая точность вычисления интеграла,
то расчет заканчивают. Значение
![]() принимают за окончательное. Иначе число
элементарных отрезков увеличивают еще
в 2 раза и снова производят расчет.
принимают за окончательное. Иначе число
элементарных отрезков увеличивают еще
в 2 раза и снова производят расчет.
Пример
5.16.
Вычислить
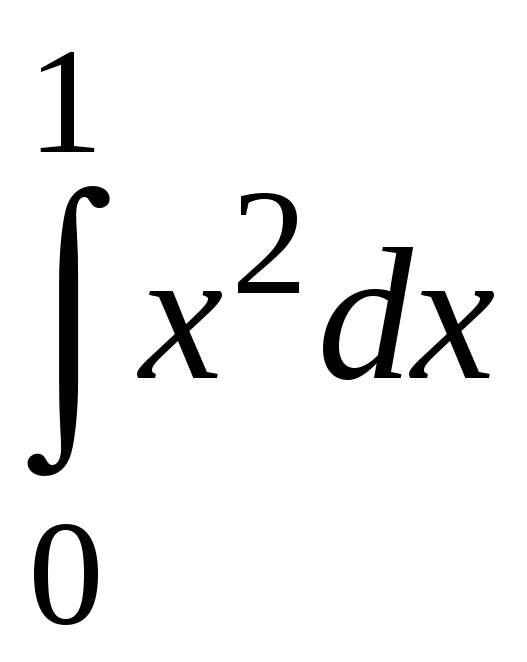 .
.
Примем
![]() .
Длина элементарных отрезков
.
Длина элементарных отрезков
![]() .
.
Вычислим значение подынтегральной функции в граничных точках элементарных отрезков
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
|
0 |
0,01 |
0,04 |
0,09 |
0,16 |
0,25 |
0,36 |
0,49 |
0,64 |
0,81 |
1,0 |
По первой формуле прямоугольников получаем
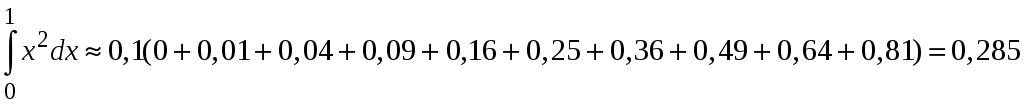 По
второй формуле прямоугольников получаем
По
второй формуле прямоугольников получаем
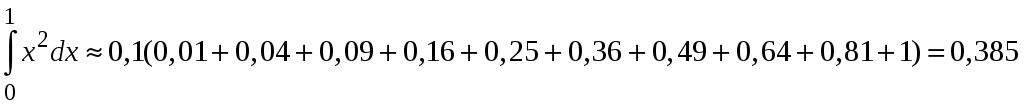
По формуле трапеций
можно получить
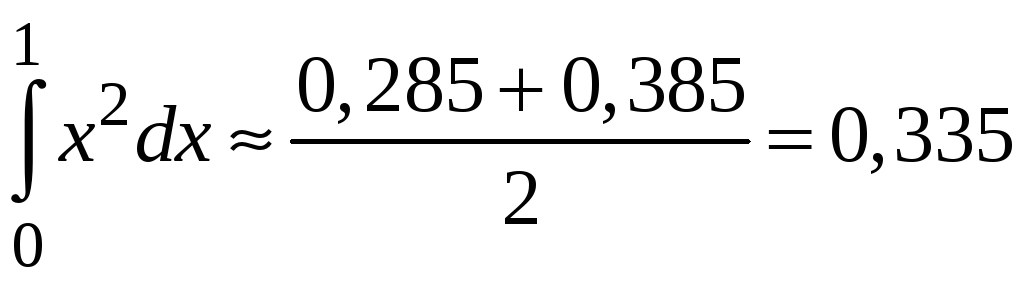 .
.
По формуле Симпсона
получим (![]() ,
,
![]() )
)
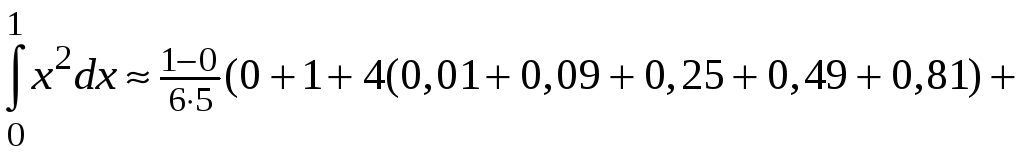
![]()
Точное значение
интеграла
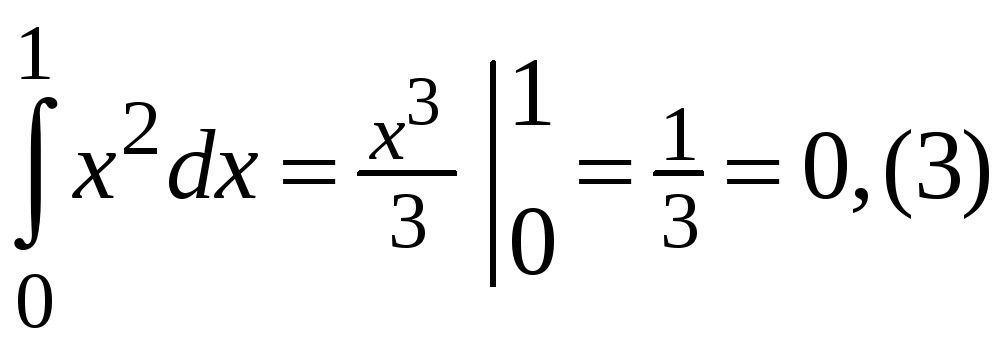 .
.
Значение интеграла,
найденное по формуле Симпсона, совпадает
с точным значением интеграла, так как
подынтегральная функция является
параболой
![]() ,
что так же предполагалось при выводе
формулы Симпсона.
,
что так же предполагалось при выводе
формулы Симпсона.

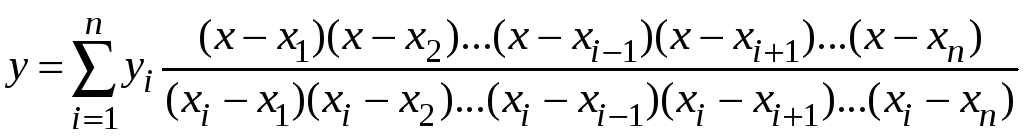 .
.