
- •Глава 5. Определенный интеграл
- •5.1. Задачи, приводящие к понятию определенного интеграла
- •5.2. Интегральные суммы, их свойства
- •Определение определенного интеграла
- •5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона - Лейбница
- •5.4. Свойства определенного интеграла
- •5.5. Методы интегрирования определенных интегралов
- •5.6. Несобственные интегралы с бесконечными пределами интегрирования
- •5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования
- •5.8. Несобственные интегралы от разрывных функций, неограниченных в точках разрыва
- •5.9. Теоремы о сходимости несобственных интегралов от разрывных функций
- •5.10. Геометрические приложения определенных интегралов
- •5.10.1. Вычисление площадей фигур
- •5.10.2. Вычисление объемов тел вращения
- •5.10.3. Длина дуги кривой
- •5.11. Численные методы нахождения определенных интегралов
- •5.11.1. Формулы прямоугольников
- •5.11.2. Формула трапеций
- •5.11.3. Формула Симпсона для приближенного вычисления определенных интегралов
- •5.12. Производная интеграла, зависящего от параметра
- •Глава 6. Двойные интегралы
- •6.1. Определение двойного интеграла
- •6.2. Геометрический смысл двойного интеграла
- •6.3. Свойства двойных интегралов
- •6.4. Вычисление двойных интегралов
- •6.5. Двойные несобственные интегралы с бесконечными пределами интегрирования
5.12. Производная интеграла, зависящего от параметра
Пусть в определенном интеграле пределы интегрирования и подынтегральная функция зависят от некоторого параметра , т.е. интеграл имеет вид
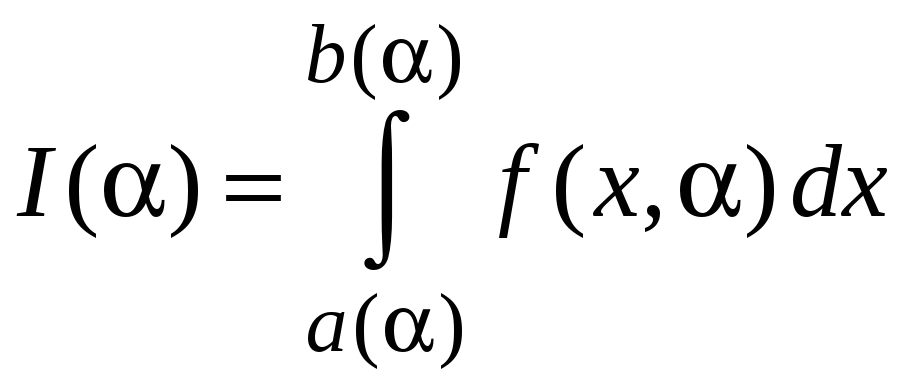 .
.
Требуется найти
производную интеграла
![]() по этому параметру .
Будем считать, что функции
по этому параметру .
Будем считать, что функции
![]() ,
,
![]() - дифференцируемые функции по .
- дифференцируемые функции по .
Рассмотрим отдельно три случая, когда в интеграле зависят от параметра либо подынтегральная функция, либо какой-то из пределов интегрирования.
1. Пусть
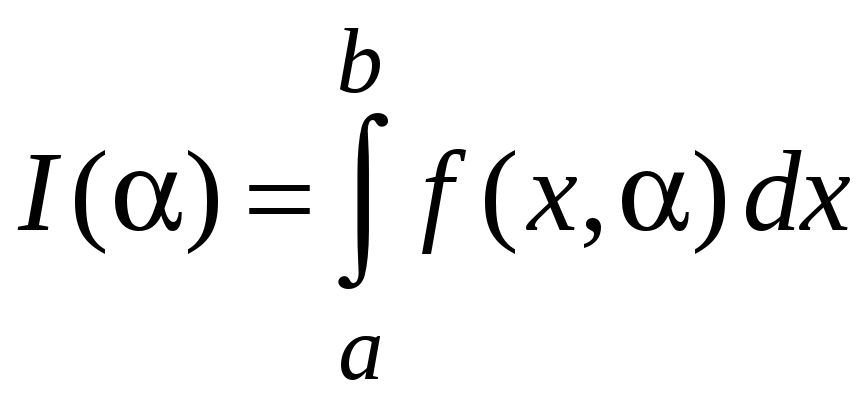 .
.
Найдем
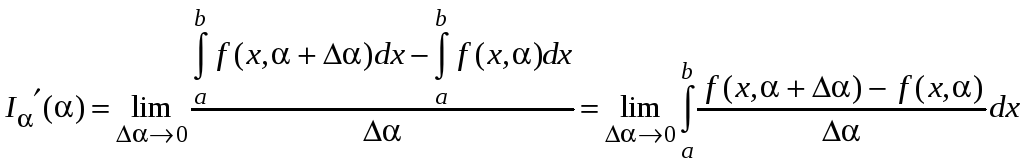
Используем теорему Лагранжа о конечном приращении функции, запишем
![]() ,
где
,
где
![]() .
.
Тогда
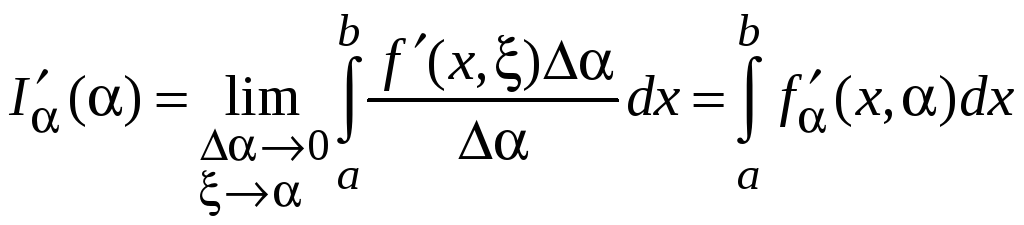 .
Следовательно,
.
Следовательно,
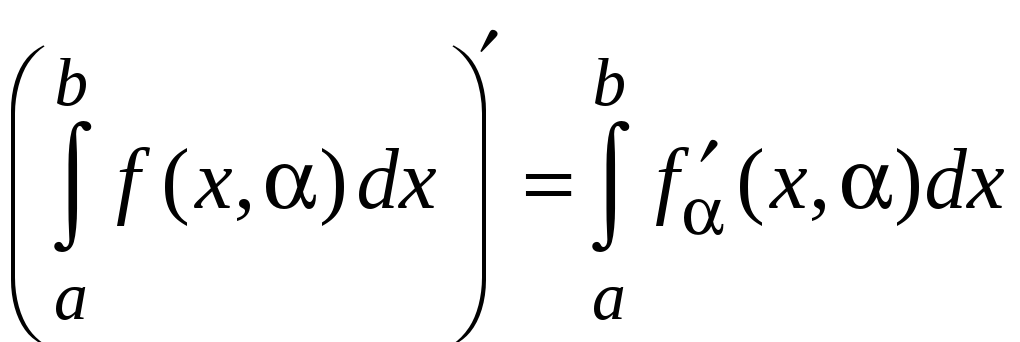 .
.
Пример
5.17.
Найти
![]() ,
если
,
если
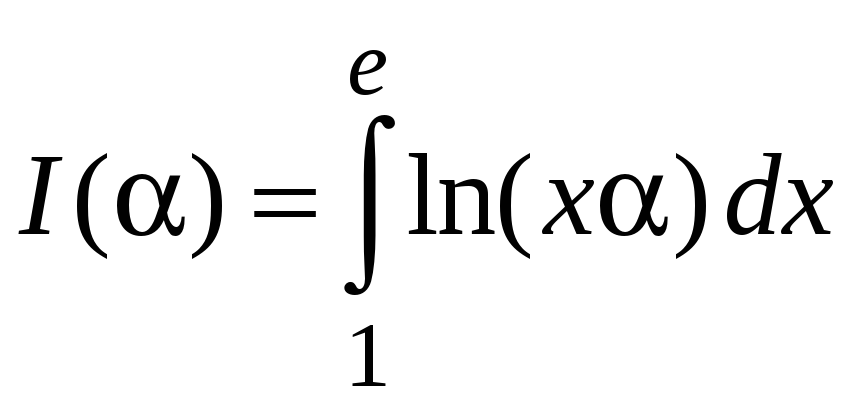 .
.
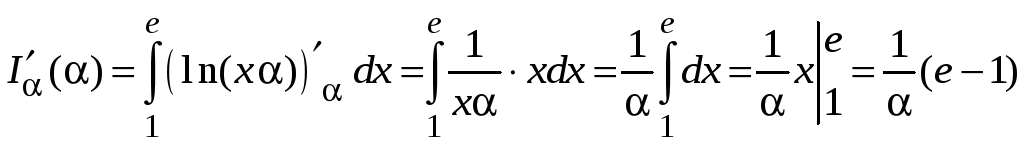 .
.
-
Пусть от параметра зависит верхний предел интегрирования, т. е.
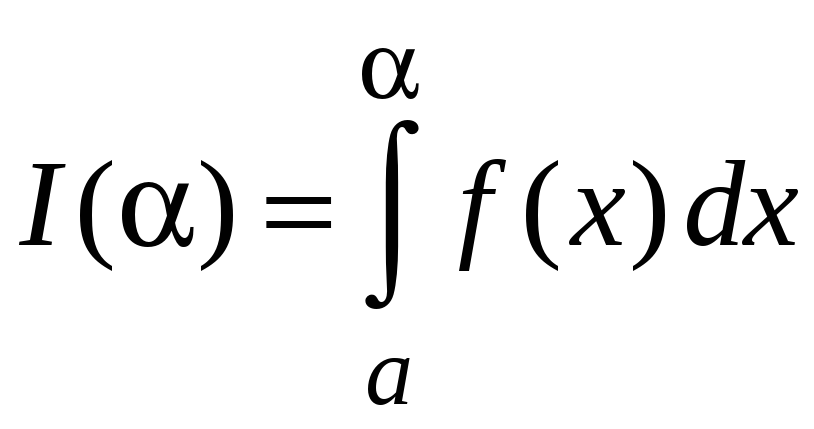 .
Найдем
.
Найдем
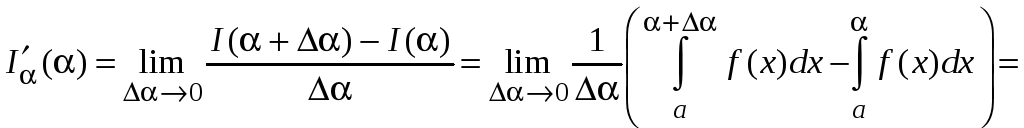
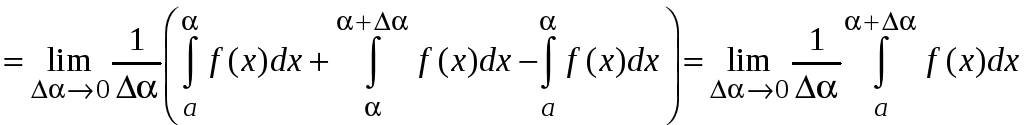 .
.
По теореме о среднем
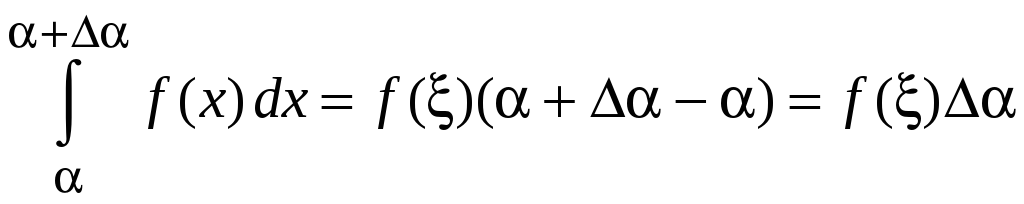 ,
где
,
где
![]() .
.
Тогда
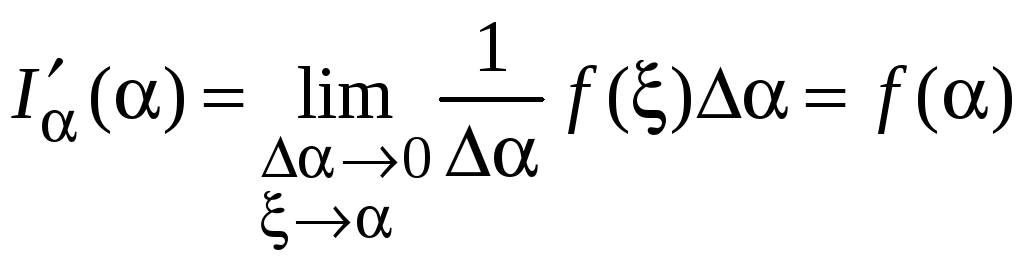 .
Следовательно,
.
Следовательно,
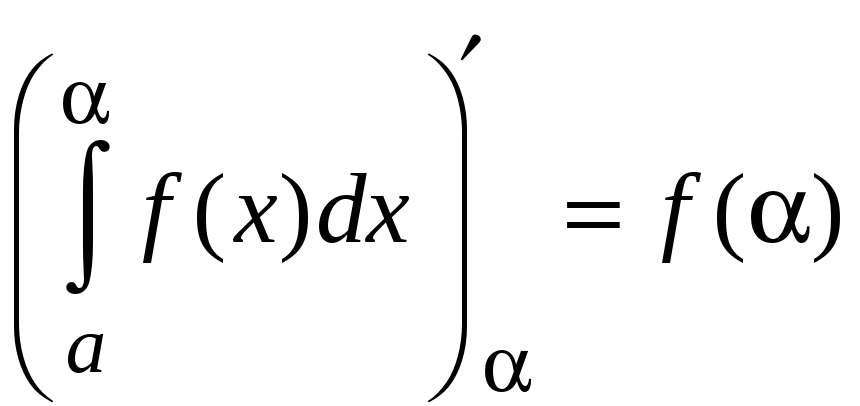 .
.
Если верхний предел
интегрирования сложная функция
![]() ,
то производная интеграла найдется как
производная сложной функции, т. е.
,
то производная интеграла найдется как
производная сложной функции, т. е.
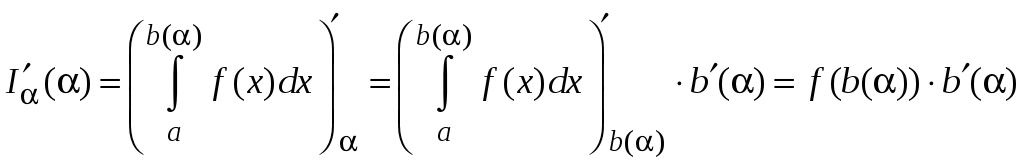 .
.
В практических
задачах нередко требуется найти
производную по x
от интеграла
 .
В этом интеграле x
под интегралом – это переменная
интегрирования, а верхний предел x
является
фактически параметром. Поэтому
.
В этом интеграле x
под интегралом – это переменная
интегрирования, а верхний предел x
является
фактически параметром. Поэтому
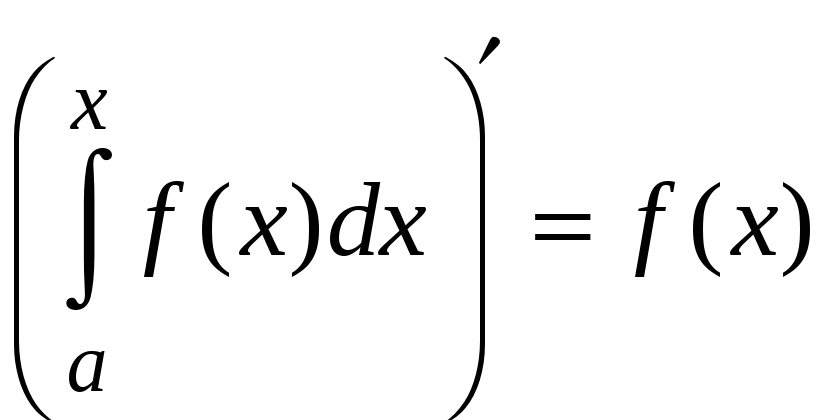 .
.
3. Если от параметра зависит только нижний предел интегрирования, то переставим верхний и нижний предел интегрирования и получим
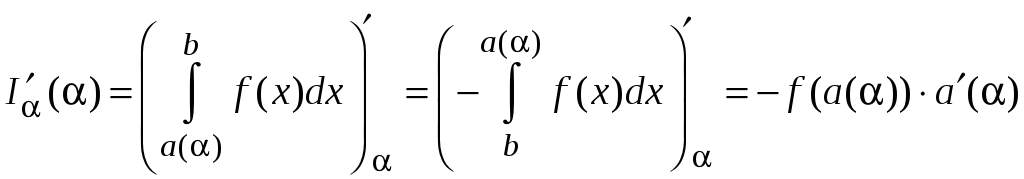 .
.
Используем формулы
дифференцирования сложной функции
нескольких переменных, получим производную
интеграла, зависящего от параметра в
общем случае
![]() или
или
 .
.
Данная формула называется формулой Лейбница.
Пример
5.18.
Найти
![]() ,
если
,
если
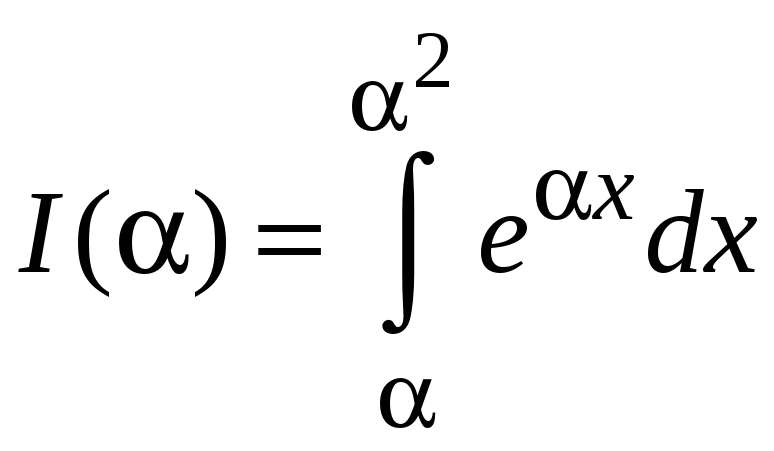 .
.
Находим
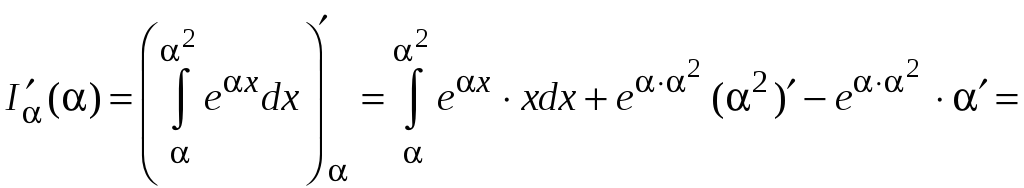
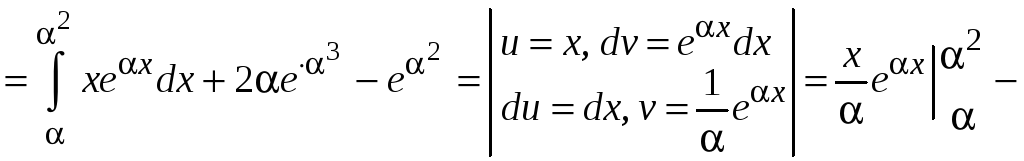
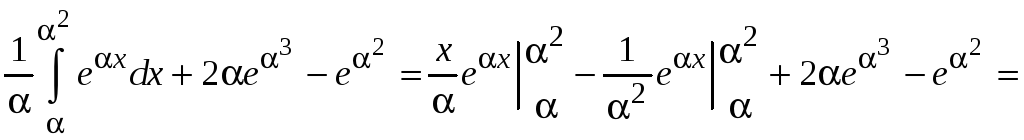
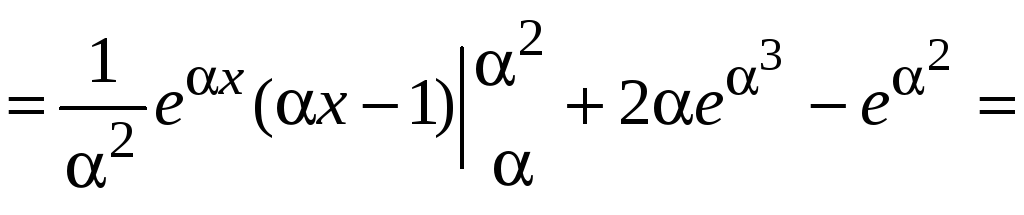
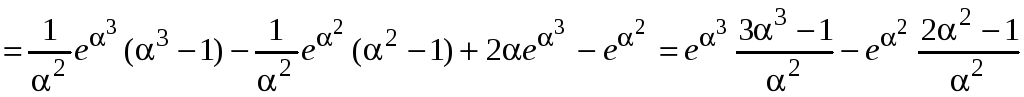 .
.
Пример
5.19.
Найти рекуррентное соотношение для
вычисления интеграла
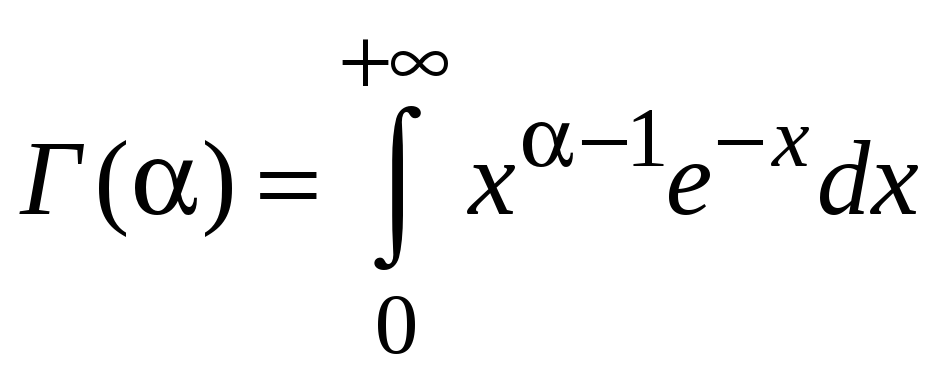 ,
зависящего от параметра.
,
зависящего от параметра.
Данный интеграл называется гамма-функцией. Он часто используется в математической статистике и других прикладных разделах высшей математики.
Найдем
 .
.
При
![]() применим интегрирование по частям.
Получим
применим интегрирование по частям.
Получим
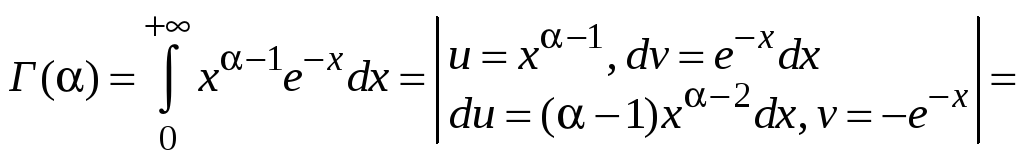
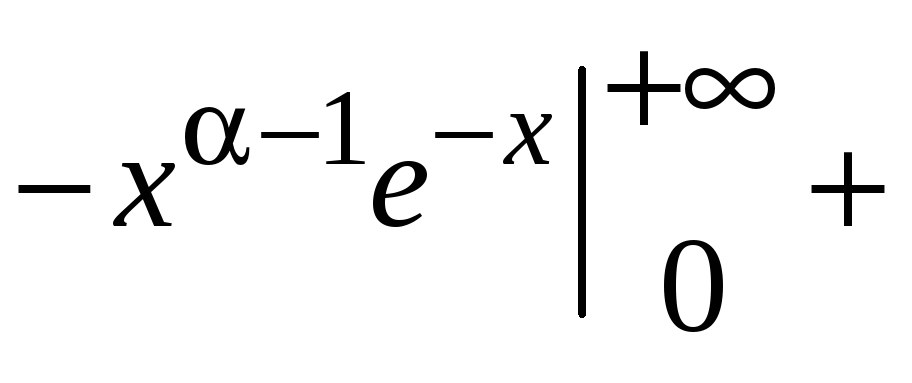
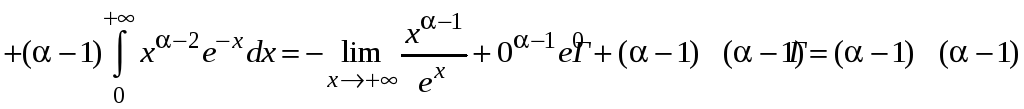 ,
,
так как
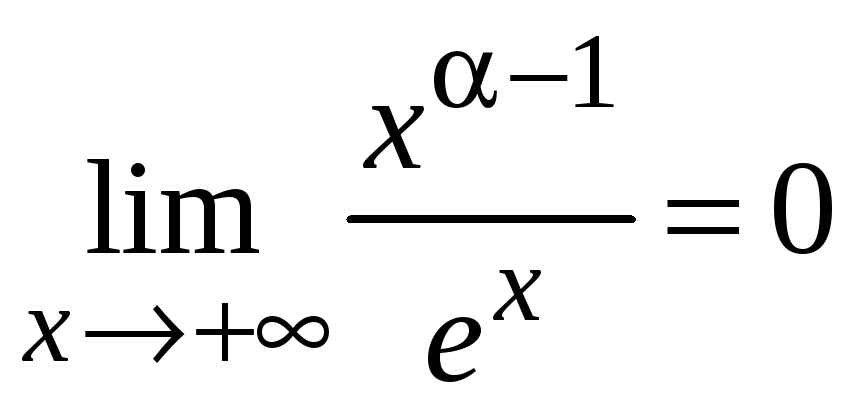 .
.
Таким образом
![]() .
.
Получим формулу
для нахождения
![]() при n
целом. Так .как.
при n
целом. Так .как.
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() и т. д.
и т. д.
![]()
Глава 6. Двойные интегралы
6.1. Определение двойного интеграла
Двойные интегралы являются обобщением понятием определенного интеграла на случай функции двух переменных.
|
|
Пусть некоторая
функция двух переменных непрерывная
и ограниченная в некоторой области
D
плоскости Оxy.
Пусть область D
ограничена конечным числом непрерывных
линий, уравнения которых имеют вид
|
Назовем диаметром
![]() элементарной области
элементарной области
![]() наибольшее расстояние между точками
этой области. В каждой элементарной
области
наибольшее расстояние между точками
этой области. В каждой элементарной
области
![]() выберем произвольно точку
выберем произвольно точку
![]() и вычислим значение функции
и вычислим значение функции
![]() .
.
Составим сумму
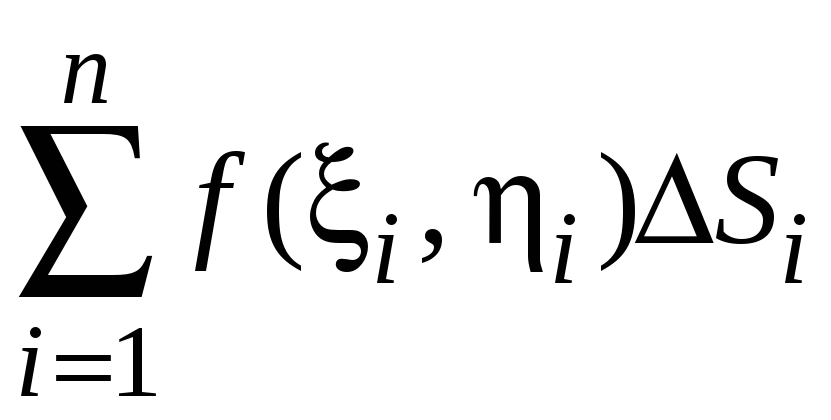 ,
которая называется интегральной.
,
которая называется интегральной.
Двойным интегралом
от функции
![]() по области D
называется предел интегральной суммы
при неограниченном увеличении числа n
элементарных областей и стремление к
нулю наибольшего их диаметра
по области D
называется предел интегральной суммы
при неограниченном увеличении числа n
элементарных областей и стремление к
нулю наибольшего их диаметра
![]() ,
т. е.
,
т. е.
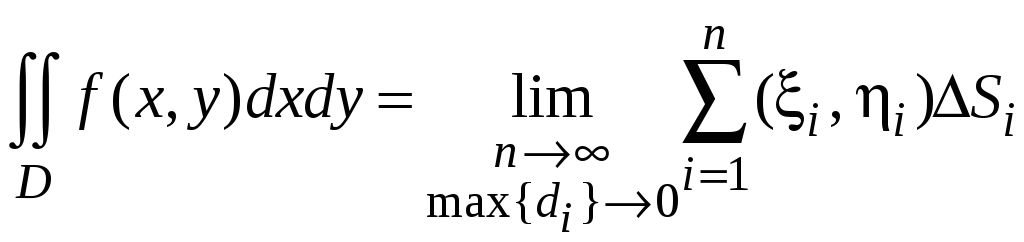 .
.

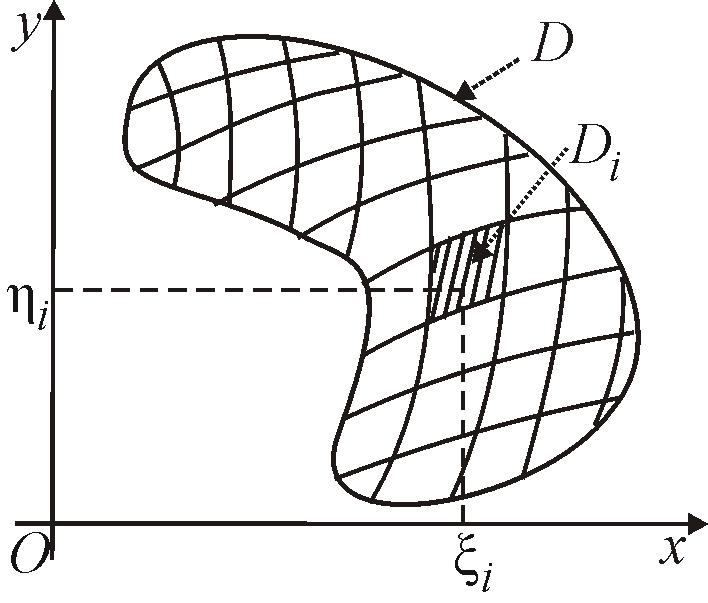 Рис. 75
Рис. 75