5.10.2. Вычисление объемов тел вращения

Рис. 67

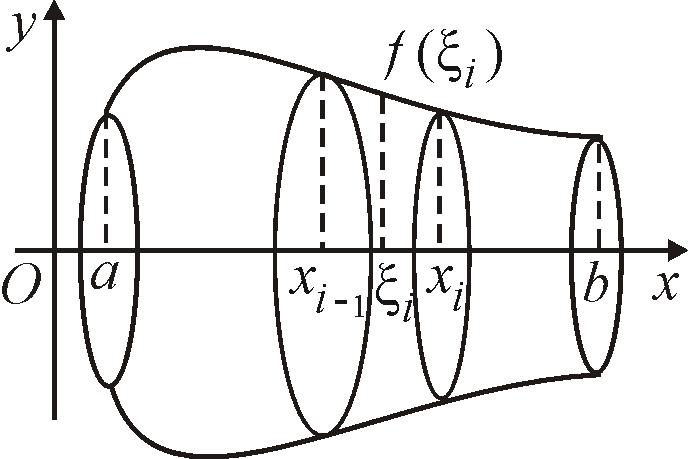
Пусть требуется вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: ) (рис. 67). Составим интегральную сумму и перейдем к пределу.

С помощью произвольно выбранных точек разобьем отрезок на n элементарных отрезков длиной i = 1, 2, …, n. Через точки деления проведем плоскости перпендикулярно оси Ох. Получим n элементарных объемов тел вращения. На каждом элементарном отрезке выберем произвольно точку и вычислим значение функции . Каждое элементарное тело вращения заменим цилиндром с радиусом основания и высотой , объем которого равен . Объем всего тела вращения приближенно равен

.

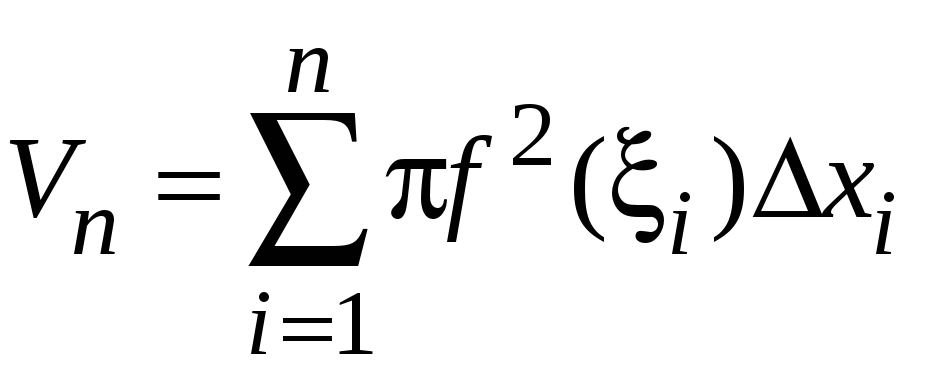Данная сумма является интегральной. Перейдем к пределу при , и получим точное значение объема

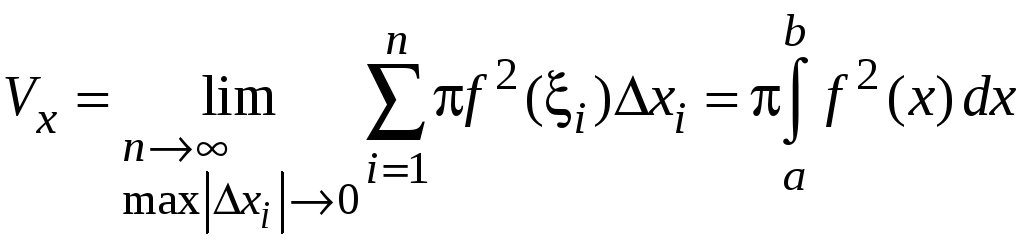
или

.

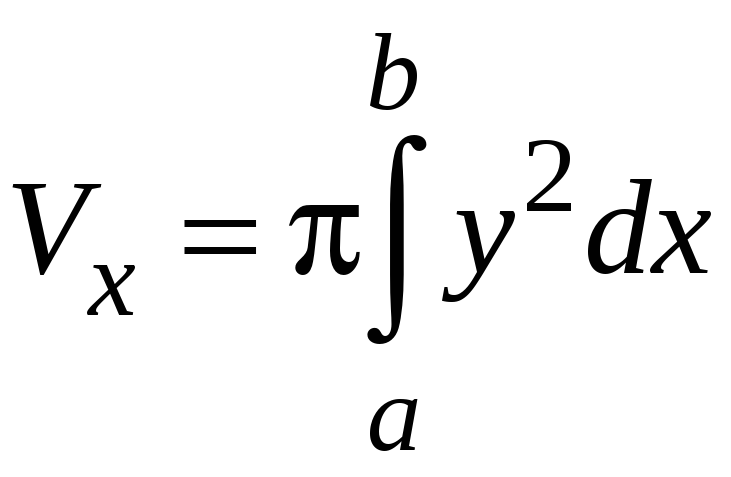Если тело образуется вращением вокруг оси Оy фигуры, ограниченной линиями: , , то его объем находится по формуле

.

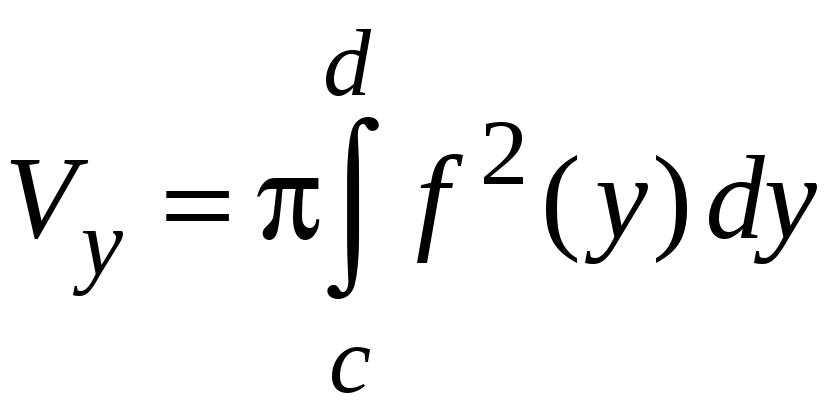Пример 5.15.

Рис. 68

Найти объем тела (рис. 68), образованного вращением вокруг оси Ох эллипса . Найдем .

Учитывая симметричность фигуры, находим объем

.

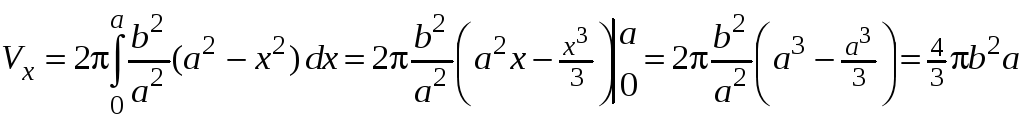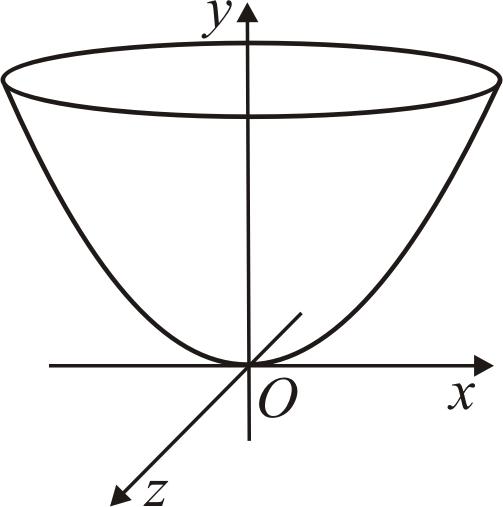
Пример 5.16. Найти объем тела, образованного вращением вокруг оси Оy фигуры, ограниченной линиями .

Рис. 69

Находим .

5.10.3. Длина дуги кривой

Требуется найти длину отрезка кривой при . Составим интегральную сумму и перейдем к пределу. Разобьем отрезок с помощью произвольно выбранных точек

на n элементарных отрезков длиной .

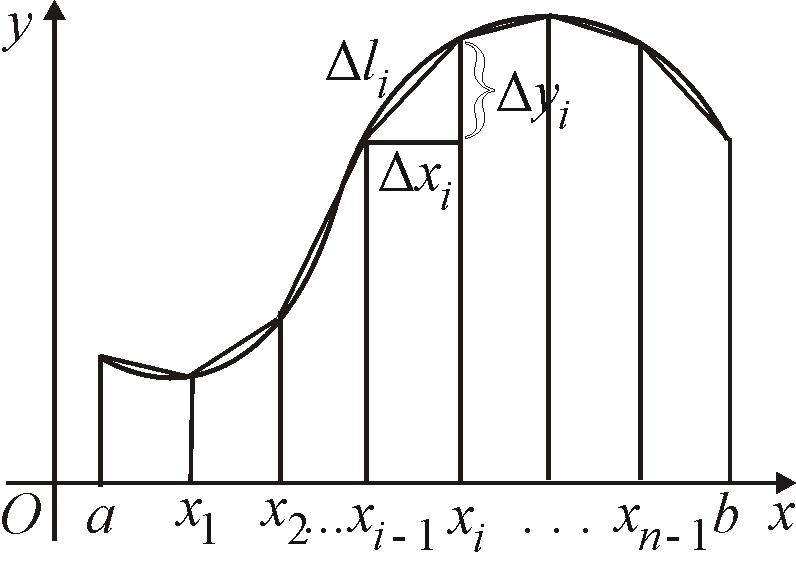
Рис. 70

На каждом элементарном отрезке заменим дугу кривой отрезком прямой (рис. 70), длина которого равна , . Используем теорему Лагранжа о конечном приращении функции на каждом элементарном отрезке. Найдем , .

Получим .

Составим интегральную сумму для нахождения приближенного значения длины дуги отрезка кривой

.

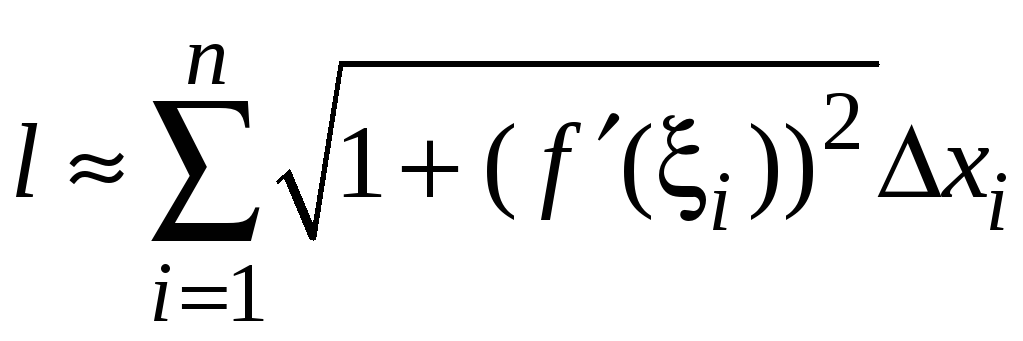Перейдем к пределу, получим точное значение длины дуги кривой

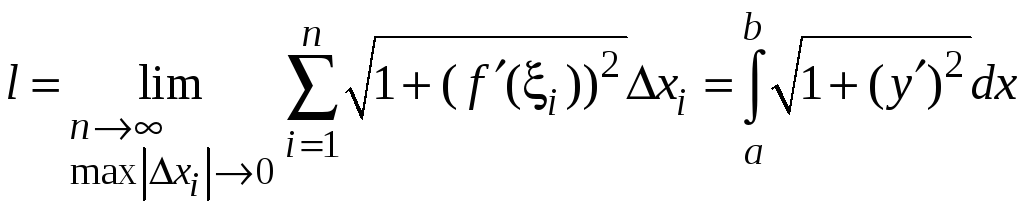
или .

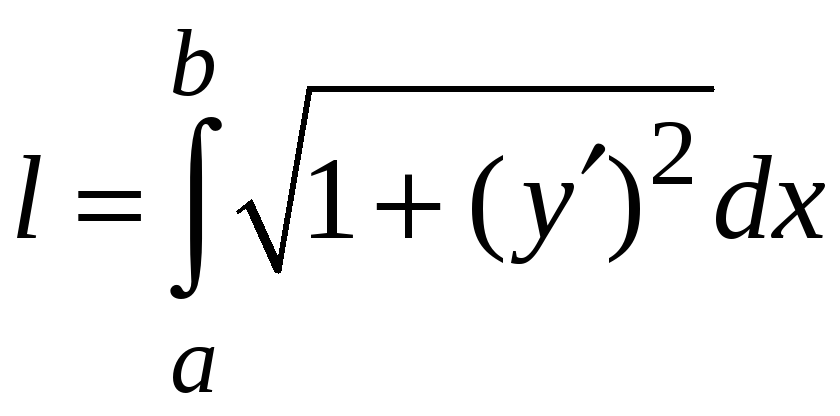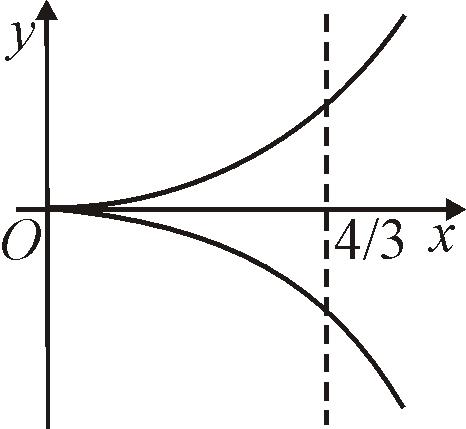
Пример 5.17. Найти длину полукубической параболы , отсекаемой прямой (рис. 71).

Рис. 71

Найдем ; . Учтем симметрию кривой, получим .

5.11. Численные методы нахождения определенных интегралов

Данные методы основываются на геометрическом смысле интеграла как площади криволинейной трапеции.

Обычно интервал интегрирования разбивают на n равных элементарных отрезков. На каждом элементарном отрезке подынтегральную функцию заменяют или прямой, или кривой задаваемого вида. Интеграл находится приближенно как сумма площадей элементарных криволинейных трапеций. В зависимости от вида функции, которой заменяют подынтегральную функцию на элементарных отрезках получают различные формулы для численных методов нахождения определенных интегралов.

Пусть требуется вычислить значение интеграла 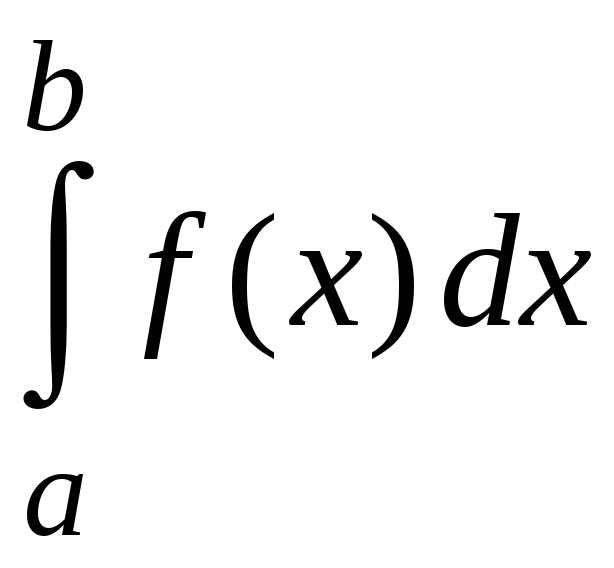. С помощью точек где , разобьем отрезок на n равных элементарных отрезков длиной h. Вычислим значения подынтегральной функции в точках деления .
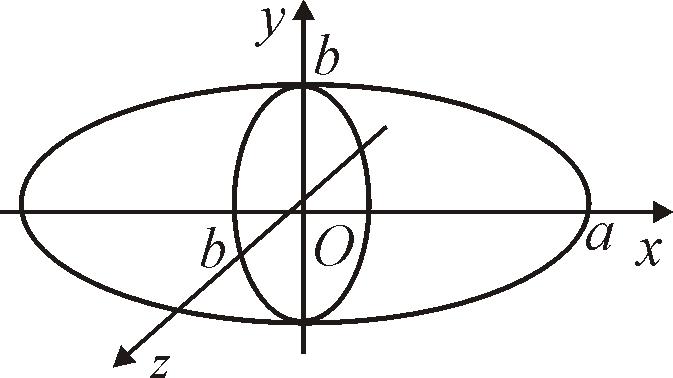
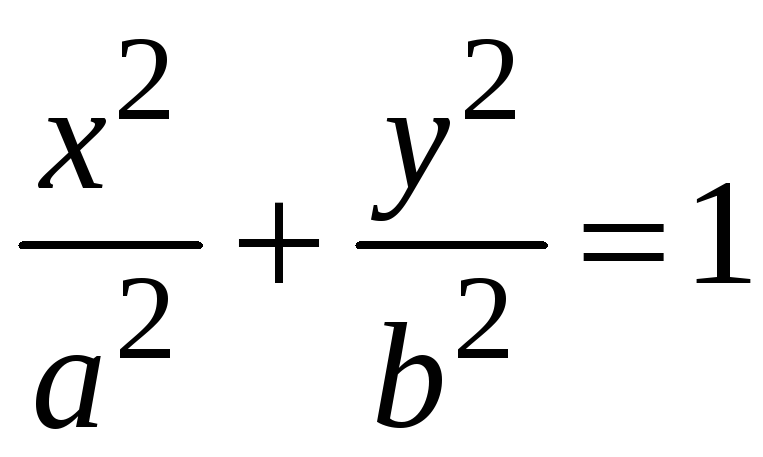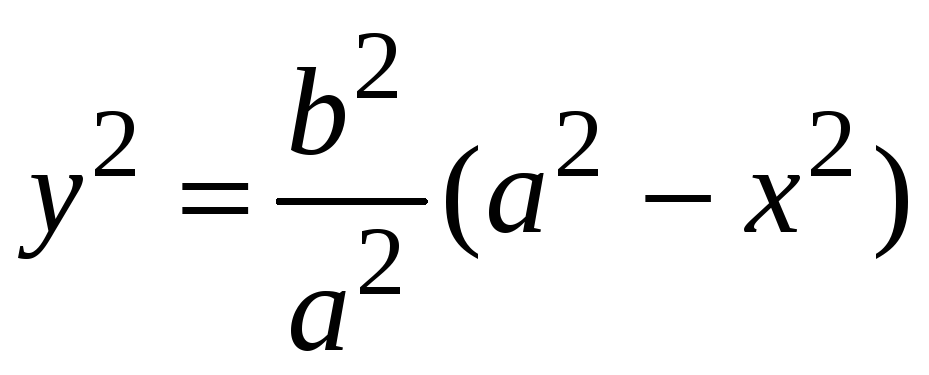
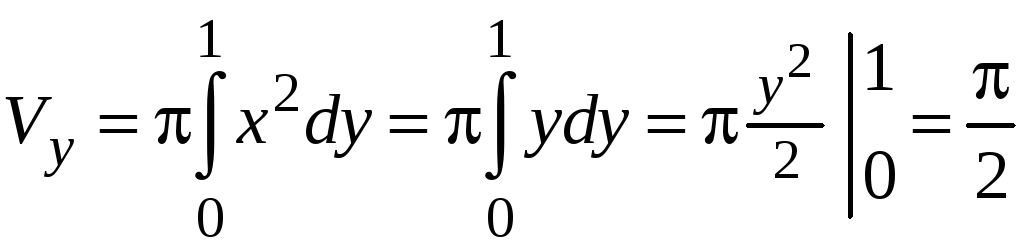
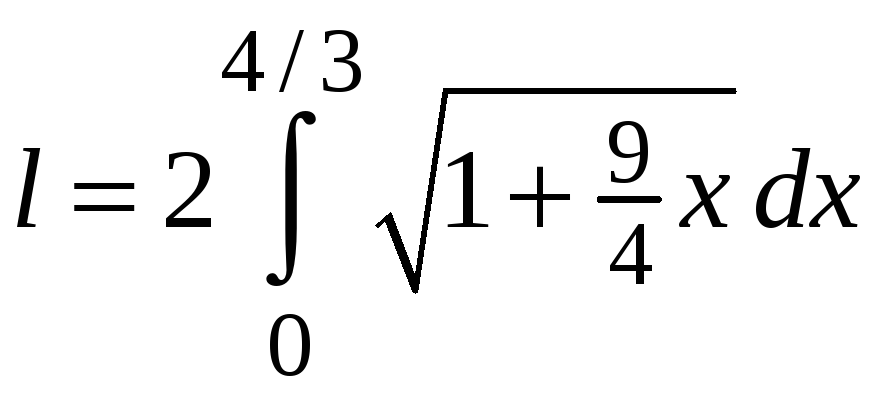
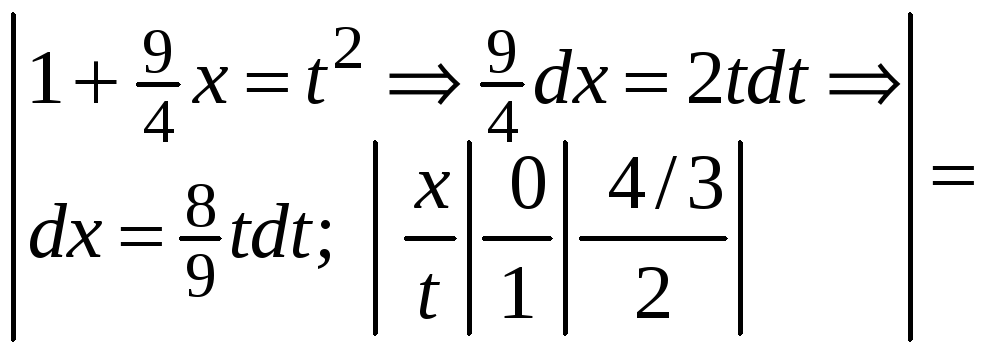
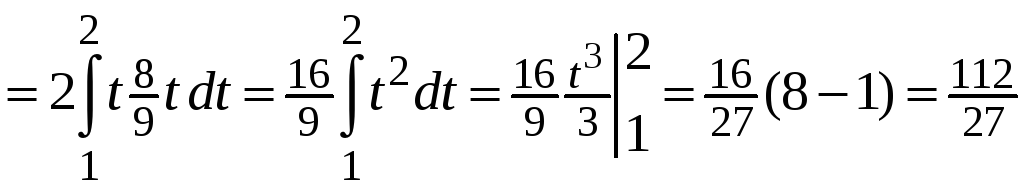