
- •Глава 7. Дифференциальные уравнения
- •7.1. Общие понятия
- •7.2. Дифференциальные уравнения первого порядка
- •7.3. Задача Коши. Теорема о существовании и единственности решения дифференциального уравнения первого порядка
- •7.4. Дифференциальные уравнения с разделяющимися переменными
- •7. 5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)
- •7.6. Линейные дифференциальные уравнения первого порядка
- •7.7. Уравнение Бернулли
- •7.8. Дифференциальные уравнения первого порядка в полных дифференциалах
- •7.9. Дифференциальные уравнения высших порядков
- •7. 10. Дифференциальное уравнение вида
- •7.11. Дифференциальные уравнения второго порядка, приводимые к дифференциальным уравнениям первого порядка
- •7.12. Линейные дифференциальные уравнения n-ого порядка. Свойства их решений
- •7.13. Линейная зависимость функций. Определитель Вронского
- •7.14. Структура общего решения линейного неоднородного дифференциального уравнения n-ого порядка
- •7.15. Комплексные числа и действия над ними
- •Действия над комплексными числами
- •7.16. Показательная функция с комплексным показателем
- •7.17. Показательная форма комплексного числа. Формула Эйлера
- •7.18. Общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.
- •7.19. Частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами
- •7.20. Метод Эйлера численного интегрирования дифференциальных уравнений
7. 5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)
Функция
![]() называется однородной n-го
измерения, если
называется однородной n-го
измерения, если
![]() ,
где t
– параметр.
,
где t
– параметр.
Например, для
функции
![]() находим
находим
![]() .
.
Следовательно, эта функция второго измерения (n = 2).
Покажем, что частное
двух однородных функций
![]() и
и
![]() одного и тоже измерения есть однородная
функция нулевого измерения. Действительно,
одного и тоже измерения есть однородная
функция нулевого измерения. Действительно,
 .
.
Однородными дифференциальными уравнениями называются уравнения вида
![]() ,
,
где
![]() и
и
![]()
однородные функции одного измерения.
однородные функции одного измерения.
Данное уравнение можно привести к уравнению с разделяющимися переменными. Для этого преобразуем уравнение
 .
.
Обозначим
 .
Тогда уравнение примет имеет вид
.
Тогда уравнение примет имеет вид
![]() ,
,
где
![]()
однородная функция нулевого измерения,
т. е.
однородная функция нулевого измерения,
т. е.
![]() .
.
Если принять
параметр
![]() ,
то
,
то
 .
.
Уравнение
![]() сводится к уравнению с разделяющимися
переменными с помощью подстановки
сводится к уравнению с разделяющимися
переменными с помощью подстановки
![]() или
или
![]() ,
,
где u = u (x) функция от x.
Найдем производную
![]() и подставим ее в уравнение, получим
и подставим ее в уравнение, получим
![]() .
.
Разделим переменные и проинтегрируем

 .
.
Решение уравнения
сведено к нахождению интегралов. В
результате интегрирования будет получен
общий интеграл
![]() .
Для нахождения общего интеграла исходного
дифференциального уравнения необходимо
сделать обратную замену переменной
.
Для нахождения общего интеграла исходного
дифференциального уравнения необходимо
сделать обратную замену переменной
![]() ,
в результате которой общий интеграл
будет иметь вид
,
в результате которой общий интеграл
будет иметь вид
![]() .
.
Пример 7.10.
Решить уравнение
![]() ;
при х =
1 y
= 1.
;
при х =
1 y
= 1.
Используем
подстановку
![]() .
Находим
.
Находим
![]() и подставляем в уравнение. Получаем
и подставляем в уравнение. Получаем
![]() .
.
Сгруппируем
отдельно слагаемые с
![]() и
и
![]()
![]()
![]() .
.
Разделим переменные и проинтегрируем


 .
.
Выполним обратную
подстановку
![]() ,
запишем общий интеграл
,
запишем общий интеграл
 .
.
Найдем значение
произвольной постоянной С,
соответствующее начальным условиям
![]() .
.
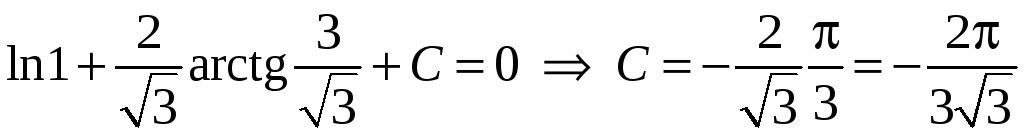 .
.
Запишем частное решение
 .
.
Пример 7.11.
Решить уравнение
![]() ;
при х
= 1
;
при х
= 1
![]() .
.
Используем
подстановку
![]() .
Найдем
.
Найдем
![]() .
Подставим y
и
.
Подставим y
и
![]() в уравнение, получим
в уравнение, получим
![]() .
.
В этом уравнении
сгруппируем в одном слагаемом
![]() ,
а в другом все остальные слагаемые,
получим
,
а в другом все остальные слагаемые,
получим
![]() .
.
Учитываем, что
![]() ,
имеем
,
имеем
![]() .
.
Разделим переменные и проинтегрируем
![]() .
.
Получаем
![]()
![]() .
.
Выполняем обратную
замену переменной
![]() ,
получаем общий интеграл
,
получаем общий интеграл
![]() .
.
Находим значение произвольной постоянной.
При
![]() получим
получим
![]()
![]() .
.
Записываем частное решение
![]() .
.
7.6. Линейные дифференциальные уравнения первого порядка
Данные уравнения в общем случае имеют вид
![]() ,
,
где
![]()
непрерывные функции.
непрерывные функции.
Разделим уравнение
на
![]() ,
получим
,
получим
![]() ,
,
где
 .
.
Известны два метода решения этих уравнений.
1. Метод замены переменной.
Искомую функцию заменяют на произведение двух функций
![]() ,
,
где
![]() ,
,
![]()
некоторые неизвестные дифференцируемые
функции.
некоторые неизвестные дифференцируемые
функции.
Подставим
![]() в уравнение, получим
в уравнение, получим
![]() .
Третье слагаемое
.
Третье слагаемое
![]() сгруппируем с одним из первых слагаемых,
либо с
сгруппируем с одним из первых слагаемых,
либо с
![]() ,
либо с
,
либо с
![]() .
Функции
.
Функции
![]() и
и
![]() входят в уравнение замены симметрично.
Пусть объединим первое и третье слагаемые
входят в уравнение замены симметрично.
Пусть объединим первое и третье слагаемые
![]() .
.
Искомой является
одна функция
![]() ,
а введены с помощью замены две
,
а введены с помощью замены две
![]() ,
,
![]() ,
поэтому одну из них, пусть
,
поэтому одну из них, пусть
![]() ,
выберем по своему усмотрению так, чтобы
,
выберем по своему усмотрению так, чтобы
![]() равнялось нулю. Тогда уравнение распадется
на два уравнения, каждое из которых с
разделяющимися переменными,
равнялось нулю. Тогда уравнение распадется
на два уравнения, каждое из которых с
разделяющимися переменными,
![]()
Необходимо сначала
решить первое уравнение, найти функцию
![]() .
Затем подставить эту функцию во второе
уравнение и решить его.
.
Затем подставить эту функцию во второе
уравнение и решить его.
Решаем первое уравнение. При решении этого уравнения достаточно найти не общее решение, а одно какое-либо частное решение

![]()
![]() .
.
Подставим найденную
функцию
![]() во второе уравнение
во второе уравнение
![]() и решим его. Найдем функцию
и решим его. Найдем функцию
![]() .
.
![]() .
.
Затем записываем
решение исходного уравнения как
произведение функций
![]() .
.
![]() .
.
Получена конечная
формула для нахождения общего решения
линейного уравнения. Однако, при решении
примеров, обычно, используют замену
![]() и повторяют приведенные выше действия.
и повторяют приведенные выше действия.
Пример
7.12.
Решить уравнение
![]() .
.
Используем
подстановку
![]() ,
получаем
,
получаем

Решаем первое уравнение системы

![]() .
.
Решаем второе
уравнение системы
![]() .
.

![]() .
.
Интеграл находим методом интегрирования по частям

![]() .
.
Находим общее
решение исходного уравнения
![]() ;
;
![]() .
.
2. Метод вариации произвольной постоянной.
Для нахождения общего решения неоднородного линейного уравнения
![]()
сначала решают соответствующее однородное уравнение
![]() .
.
Данное уравнение с разделяющимися переменными. Решая его, получим


![]()
![]() .
.
Далее, произвольную
постоянную
![]() заменяют на функцию
заменяют на функцию
![]() и ищут решение исходного неоднородного
уравнения в виде
и ищут решение исходного неоднородного
уравнения в виде
![]() .
.
Теперь, чтобы
получить решение уравнения, необходимо
найти функцию
![]() .
Найдем производную функции
.
Найдем производную функции
![]() .
.
![]()
![]() .
.
Подставим функцию
![]() и ее производную в исходное неоднородное
уравнение
и ее производную в исходное неоднородное
уравнение
![]() .
.
![]() .
.
Второе и третье
слагаемые в левой части этого уравнения
уничтожаются, получается дифференциальное
уравнение относительно функции
![]() с разделяющимися переменными
с разделяющимися переменными
![]() .
.
Разделяем переменные и интегрируем
![]() ,
,
где С – произвольная постоянная.
Записываем решение исходного неоднородного уравнения
![]() .
.
Пример
7.13 .
Найти общее решение уравнения
![]() .
.
Используем метод вариации произвольной постоянной. Решим соответствующее исходному однородное уравнение

 .
.
Ищем решение
исходного неоднородного уравнения в
виде
![]() .
Подставляем эту функцию в исходное
уравнение
.
Подставляем эту функцию в исходное
уравнение
![]() .
.
Получаем уравнение
для нахождения
![]()
![]() .
.
Решаем это уравнение
![]() .
.
Находим

![]() .
.
Записываем решение исходного уравнения
![]()
или
![]() .
.
