Действия над комплексными числами
1. Сложение (вычитание) комплексных чисел.
,
т. е. при сложении (вычитании) комплексных чисел их действительные и мнимые части складываются (вычитаются).
2. Умножение комплексных чисел.
Комплексные числа перемножаются как двучленны; при этом необходимо учитывать, что
,
,
.
Умножим два комплексных числа, имеем
.
Получим произведение комплексных чисел в тригонометрическом виде
.
Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
В частном случае, при умножении двух комплексно-сопряженных чисел получается квадрат их модуля.
.
Следствие. Возведение в степень комплексного числа.
Если
,
то
,
т. е. при возведении комплексного числа в n-ю степень его модуль возводится в эту степень, а аргумент умножается на эту степень.
Например
.
3. Деление комплексных чисел.
Запишем в
координатном виде
.
Умножим числитель и знаменатель на число комплексно-сопряженное знаменателю, получим
.
Более удобный вид частного комплексных чисел получим при использовании тригонометрической записи.
.
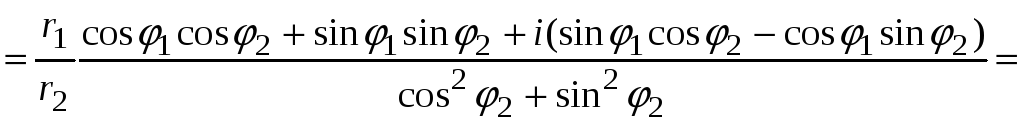
Следовательно, при делении комплексных чисел их модули делятся, а аргументы вычитаются.
4. Извлечение корня из комплексного числа.
Пусть
,
а
.
Равенство
возведем в n-ю
степень, получим
Отсюда получим для модулей чисел равенство
или
.
Аргументы равных
чисел могут отличаться на число, кратное
2,
поэтому для аргументов чисел z
и
имеем
,
.
Следовательно,
.
Корень n-ой
степени из действительного числа А,
отличного от нуля, имеет n
значений, так как действительное число
является частным случаем комплексного
и может быть представлено в
тригонометрической форме: если
,
то
,
если
,
то
.
Пример 7.19.
Найти корень кубический из комплексной
единицы
.
Представим эту единицу в тригонометрическом
виде
.
Получаем
=
.
При
имеем корень
.
При
корень
.
При
корень
.
|
Рис. 84 |
Таким
образом, корень кубический из единицы
|
в комплексной плоскости имеет три
значения:
,
,
,
которые изображены точками на рис.
84. Все корни имеют один и тот же модуль,
равный единице, поэтому они располагаются
на окружности. Аргументы корней равны:
0,
120
и 240,
поэтому они делят окружность на три
равных части.
Пример 7.20.
Найти
.
Получаем
.
;
;
;
;
Пример 7.21.
Решить уравнение
.
Находим
.
7.16. Показательная функция с комплексным показателем
Величина
называется комплексной переменной,
если x,
y
– действительные переменные, а
.
Комплексная переменная w называется функцией комплексной переменной z с областью определения D и множеством значений Е, если для любого z, принадлежащего множеству D соответствует единственное значение w, принадлежащее множеству Е.
Записывают
или
.
Функция
или
называется показательной функцией
комплексной переменной.
По определению показательной функции с комплексным показателем
.
Например,
,
,
,
.
Показательная функция комплексного переменного обладает всеми теми же свойствами, что и показательная функция действительного переменного.
Покажем, например, что при умножении показательных функций их показатели складываются. Найдем
.
.
Следовательно
.
Аналогично можно показать следующее:
1)
;
2)
,
где m
Z;
3)
.
Комплексная величина
,
где
действительные функции действительной
переменной х,
называется комплексной функцией
действительной переменной.
Если существуют
производные
,
то выражение
называется производной комплексной функции действительной переменной.
Найдем производную
показательной функции
,
где a
и b
– действительные числа. Эту функцию
можно записать в виде
,
т. е. она является комплексной функцией действительной переменной.
Найдем производную этой функции
.
Следовательно,
.