- •Глава 7. Дифференциальные уравнения
- •7.1. Общие понятия
- •7.2. Дифференциальные уравнения первого порядка
- •7.3. Задача Коши. Теорема о существовании и единственности решения дифференциального уравнения первого порядка
- •7.4. Дифференциальные уравнения с разделяющимися переменными
- •7. 5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)
- •7.6. Линейные дифференциальные уравнения первого порядка
- •7.7. Уравнение Бернулли
- •7.8. Дифференциальные уравнения первого порядка в полных дифференциалах
- •7.9. Дифференциальные уравнения высших порядков
- •7. 10. Дифференциальное уравнение вида
- •7.11. Дифференциальные уравнения второго порядка, приводимые к дифференциальным уравнениям первого порядка
- •7.12. Линейные дифференциальные уравнения n-ого порядка. Свойства их решений
- •7.13. Линейная зависимость функций. Определитель Вронского
- •7.14. Структура общего решения линейного неоднородного дифференциального уравнения n-ого порядка
- •7.15. Комплексные числа и действия над ними
- •Действия над комплексными числами
- •7.16. Показательная функция с комплексным показателем
- •7.17. Показательная форма комплексного числа. Формула Эйлера
- •7.18. Общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.
- •7.19. Частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами
- •7.20. Метод Эйлера численного интегрирования дифференциальных уравнений
7.13. Линейная зависимость функций. Определитель Вронского
Функции
![]() называются линейно независимыми в
области G,
если линейная комбинация этих функций
равна нулю
называются линейно независимыми в
области G,
если линейная комбинация этих функций
равна нулю
![]()
при любом значении
![]() только при нулевом наборе чисел
только при нулевом наборе чисел
![]() .
.
В противном случае эти функции называются линейно зависимыми.
Для определения линейной зависимости функций используется определитель Вронского, который имеет вид
 .
.
Теорема 7.3.
Решения линейного однородного
дифференциального уравнения
![]() являются линейно зависимыми в некоторой
области G,
если для любого значения x
из этой области (
являются линейно зависимыми в некоторой
области G,
если для любого значения x
из этой области (![]() )
определитель Вронского тождественно
равен нулю
)
определитель Вронского тождественно
равен нулю
![]() ,
и, наоборот, решения уравнения
,
и, наоборот, решения уравнения
![]() линейно независимые, если
линейно независимые, если
![]() .
.
Например, покажем,
что функции
![]() и
и
![]() являющиеся решениями дифференциального
уравнения
являющиеся решениями дифференциального
уравнения
![]() ,
являются линейно независимые. Найдем
для этих функций определитель Вронского
,
являются линейно независимые. Найдем
для этих функций определитель Вронского
 .
.
Определитель отличен от нуля. Следовательно, функции линейно независимые.
7.14. Структура общего решения линейного неоднородного дифференциального уравнения n-ого порядка
Линейному неоднородному дифференциальному уравнению n-ого порядка
![]()
соответствует однородное дифференциальное уравнение
![]() .
.
Пусть линейно
независимые функции
![]() являются решениями линейного однородного
дифференциального уравнения
являются решениями линейного однородного
дифференциального уравнения
![]() .
.
Покажем, что
![]() ,
где
,
где
![]()
произвольно заданные постоянные,
является общим решением этого уравнения.
Для этого необходимо убедиться в том,
что при любых начальных условиях можно
выбрать произвольные постоянные
произвольно заданные постоянные,
является общим решением этого уравнения.
Для этого необходимо убедиться в том,
что при любых начальных условиях можно
выбрать произвольные постоянные
![]() так, чтобы функция
так, чтобы функция
![]() была частным решением дифференциального
уравнения с этими начальными условиями.
была частным решением дифференциального
уравнения с этими начальными условиями.
Пусть начальные условия имеют вид
![]() .
.
Составим систему
уравнений для нахождения произвольных
постоянных
![]() .
.

Эта система является системой линейных алгебраических уравнений.
Определитель данной системы представляет собой определитель Вронского
 .
.
Этот определитель
отличен от нуля, так как функции
![]() линейно независимые. Решение системы
(набор значений произвольных постоянных
линейно независимые. Решение системы
(набор значений произвольных постоянных
![]() )
можно получить с помощью формул Крамера.
Система имеет единственное решение.
)
можно получить с помощью формул Крамера.
Система имеет единственное решение.
Следовательно, общее решение линейного однородного дифференциального уравнения n-го порядка можно найти как линейную комбинацию n линейно независимых его частных решений.
Таким образом, справедлива следующая теорема.
Теорема 7.4.
Общее решение линейного неоднородного
дифференциального уравнения n-ого
порядка
![]() равняется сумме общего решения
соответствующего однородного уравнения
равняется сумме общего решения
соответствующего однородного уравнения
![]() и частного решения этого неоднородного
уравнения, т. е.
и частного решения этого неоднородного
уравнения, т. е.
 ,
,
где
![]()
линейно независимые решения однородного
уравнения
линейно независимые решения однородного
уравнения
![]() ,
,
![]() частное решение
неоднородного уравнения
частное решение
неоднородного уравнения
![]() .
.
7.15. Комплексные числа и действия над ними
Для нахождения решения часто встречающихся в практических исследованиях дифференциальных уравнений n-го порядка с постоянными коэффициентами необходимо рассмотреть комплексные числа и действия над ними.
Комплексным числом называется выражение вида
![]() ,
,
где
![]()
реальная часть z
(действительное число),
реальная часть z
(действительное число),
![]() мнимая часть z,
мнимая часть z,
![]() мнимая единица.
мнимая единица.
Два комплексных
числа
![]() и
и
![]() равны, если
равны, если
![]() ,
,
![]() .
.
Комплексное число
равно нулю, если
![]() .
.
Два числа
![]() и
и
![]() называются комплексно-сопряженными.
называются комплексно-сопряженными.
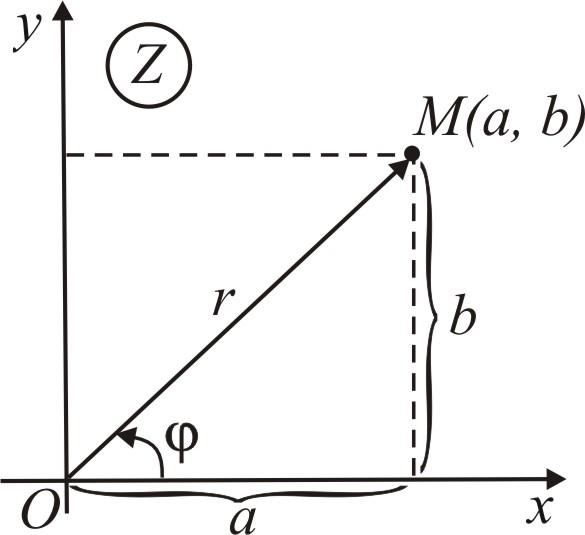
|
Рис. 83 |
Любое комплексное
число
|
Тогда можно записать
 или
или

Угол
![]() называется аргументом комплексного
числа. Аргумент определяется неоднозначно,
а с точностью до слагаемого
называется аргументом комплексного
числа. Аргумент определяется неоднозначно,
а с точностью до слагаемого
![]() .
Сопряженные комплексные числа
.
Сопряженные комплексные числа
![]() и
и
![]() имеют равные модули
имеют равные модули
![]() ,
а
,
а
![]() .
Любое комплексное число можно записать
в тригонометрическом виде
.
Любое комплексное число можно записать
в тригонометрическом виде
![]() ,
т. е.
,
т. е.
![]() .
.
Данный вид записи позволяет облегчить действия над комплексными числами.