
- •Глава 8. Числовые ряды
- •8.1. Основные понятия
- •8.1. 1. Определение числового ряда
- •8.1.2. Сходимость числового ряда. Сумма ряда
- •8.1.3. Свойства сходящихся рядов
- •8.2. Необходимый признак сходимости числового ряда
- •8.4.2. Признак Даламбера сходимости знакоположительных рядов
- •8.4.3. Радикальный признак Коши сходимости числового ряда
- •8.4.4. Интегральный признак Коши
- •8.5. Знакочередующиеся ряды. Теорема Лейбница
- •8.6. Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда
- •Глава 9. Степенные ряды
- •9.1. Функциональные ряды. Общие понятия
- •9.2. Равномерная сходимость функциональных рядов. Теорема Вейерштрасса
- •9.3. Теорема Абеля о виде области сходимости степенного ряда
- •9.4. Радиус и область сходимости степенного ряда
- •9.5. Ряды Тейлора и Маклорена
- •9.6. Разложение в ряд Маклорена основных элементарных функций
- •9.7. Применение рядов для приближенных вычислений
- •Вопросы к экзамену Неопределённый интеграл
- •Определённый интеграл
- •77. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница. Гамма-функция. Дифференциальные уравнения
- •Шершнев Владимир Григорьевич математический анализ
- •Часть 2. Интегральное исчисление
- •117997, Москва, Стремянный пер. 36.
9.5. Ряды Тейлора и Маклорена
Функция
![]() разлагается в степенной ряд
разлагается в степенной ряд
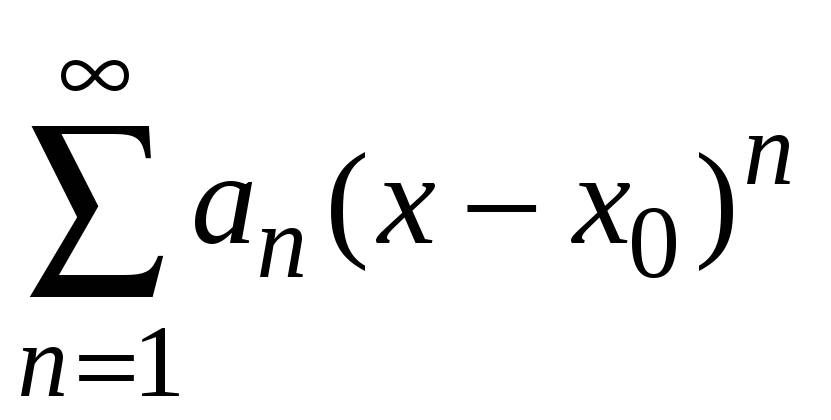 в области G,
если он составлен для этой функции и
сходится к ней.
в области G,
если он составлен для этой функции и
сходится к ней.
Пусть степенной ряд
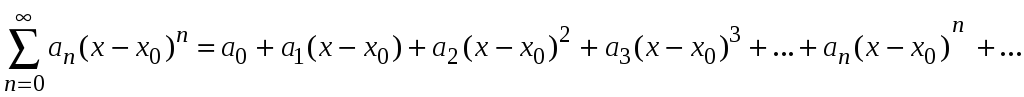
Равномерно сходится
к функции
![]() ,
т. е.
,
т. е.
![]()
![]()
Тогда его можно почленно дифференцировать.
Найдем производные этого ряда.
![]() ;
;
![]() ;
;
![]() ;
;
………………………………………………………………………………………
![]()
![]()
……………………………………………………………………………………………………
Подставим значение
![]() в эти соотношения
в эти соотношения
![]() ,получим
формулы для нахождения коэффициентов
,получим
формулы для нахождения коэффициентов
![]()
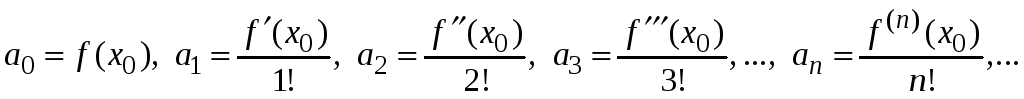
Следовательно,
![]()
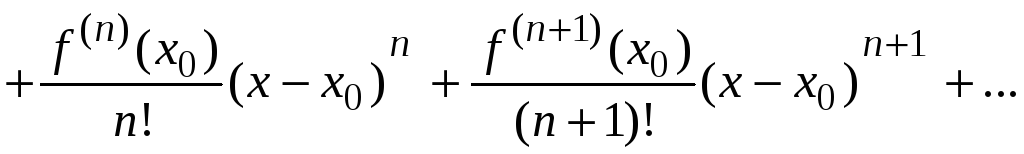
Данный ряд называется рядом Тейлора.
При
![]() данный ряд имеет вид
данный ряд имеет вид
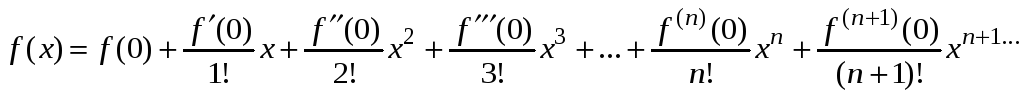
и называется рядом Маклорена.
Разложения функций по данным формулам справедливы только в области сходимости этих рядов.
Ранее были получены формулы Тейлора и Маклорена (Математический анализ. Часть 1. Дифференциальное исчисление).
В формуле Тейлора
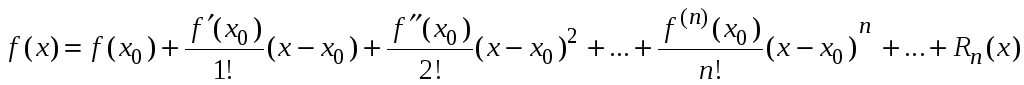
остаточный член
![]() можно рассматривать как остаточный
член ряда Тейлора. В форме Лагранжа он
имеет вид
можно рассматривать как остаточный
член ряда Тейлора. В форме Лагранжа он
имеет вид
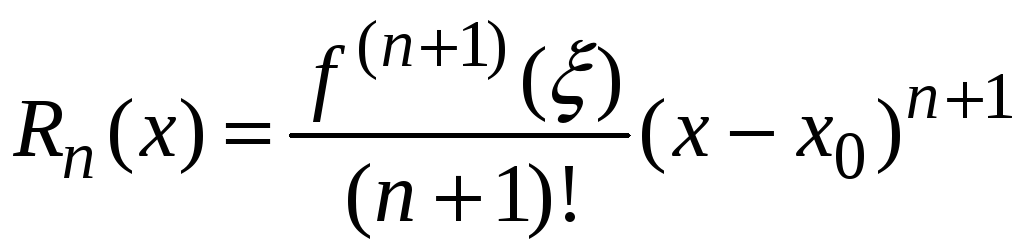 ,
,
где
![]() или
или
![]() .
.
Также для ряда Маклорена
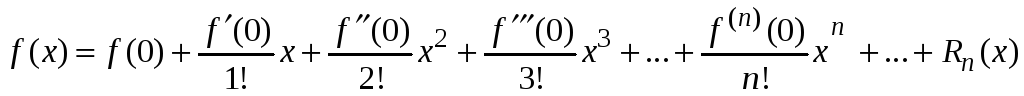
остаточный член в форме Лагранжа имеет вид
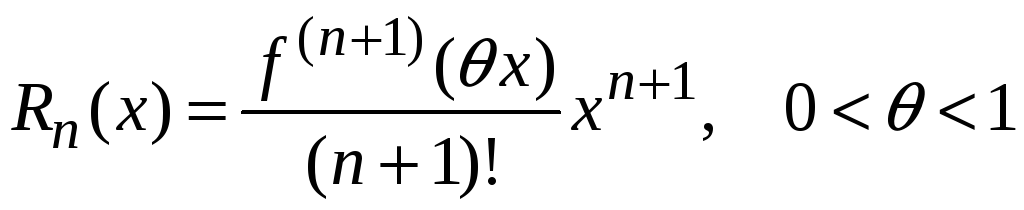 .
.
Теорема 9.2.
Для того чтобы степенной ряд
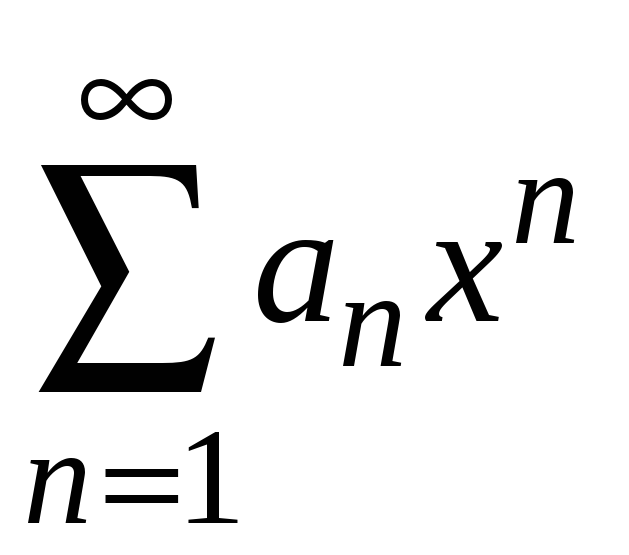 сходился к функции
сходился к функции
![]() ,
для которой он составлен, необходимо и
достаточно, чтобы остаточный член ряда
стремился к нулю при неограниченном
увеличении его номера n,
т. е.
,
для которой он составлен, необходимо и
достаточно, чтобы остаточный член ряда
стремился к нулю при неограниченном
увеличении его номера n,
т. е.
![]() .
.
Д о к а з а т е л ь с т в о.
Необходимость.
Пусть ряд
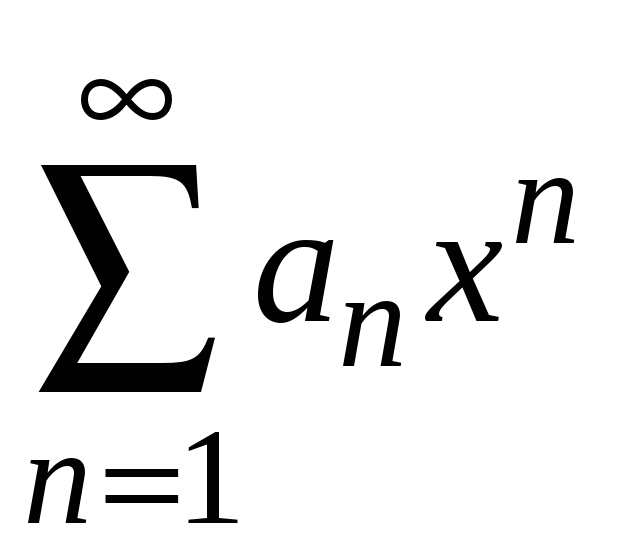 сходится к функции
сходится к функции
![]() ,
т. е.
,
т. е.
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Достаточность.
Пусть
![]() .
.
Тогда
![]() ,
,
т. е. ряд сходится.
9.6. Разложение в ряд Маклорена основных элементарных функций
Принимая во внимание
полученные ранее формулы Маклорена для
функций
![]() можем записать ряды для этих функций и
найти их области сходимости.
можем записать ряды для этих функций и
найти их области сходимости.
-
Функция
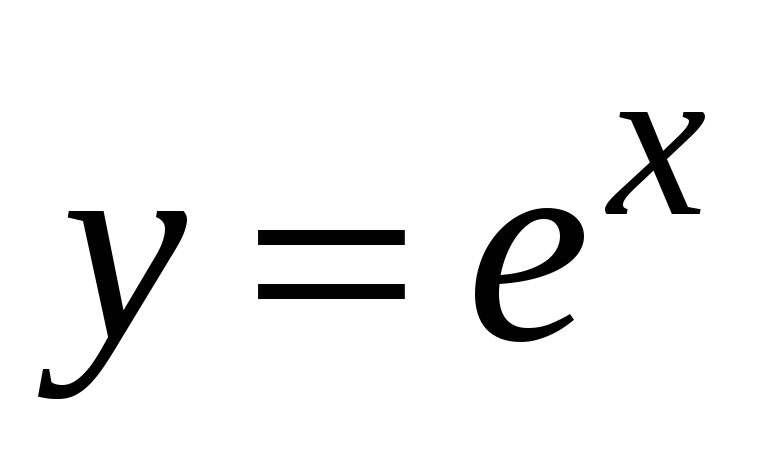 .
Ряд Маклорена имеет вид
.
Ряд Маклорена имеет вид
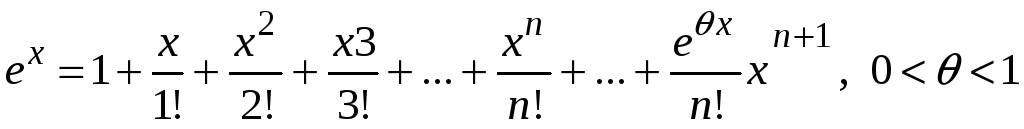 .
.
Найдем радиус сходимости ряда
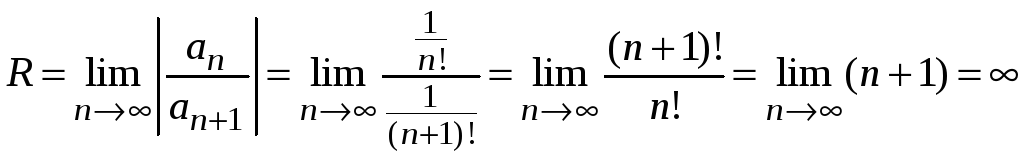 .
.
Область сходимости
ряда
![]() .
.
2. Функция
![]() .
Ряд Маклорена имеет вид
.
Ряд Маклорена имеет вид
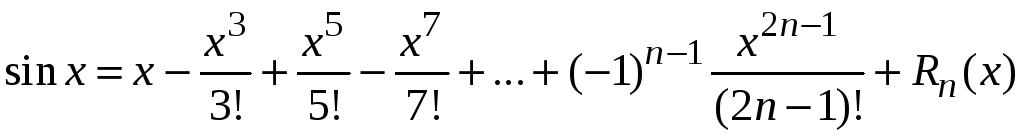 ,
,
где
![]()
остаточный член, записанный в данном
случае в форме Пеано. Запись
остаточный член, записанный в данном
случае в форме Пеано. Запись
![]() означает, что функция
означает, что функция
![]() является бесконечно малой по сравнению
с функцией
является бесконечно малой по сравнению
с функцией
![]() .
.
Найдем радиус сходимости этого ряда
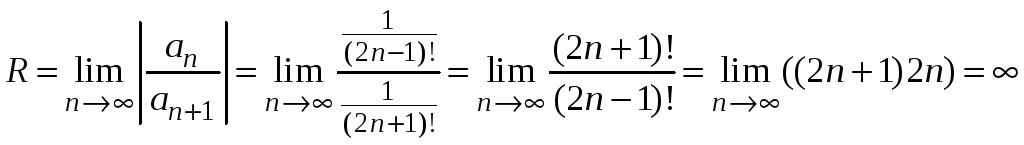 .
.
Область сходимости
ряда
![]() .
.
3. Функция
![]() .
Ряд Маклорена имеет вид
.
Ряд Маклорена имеет вид
 ,
,
где
![]()
остаточный член. Здесь нумерация членов
ряда начинается с n
= 0.
остаточный член. Здесь нумерация членов
ряда начинается с n
= 0.
Радиус сходимости
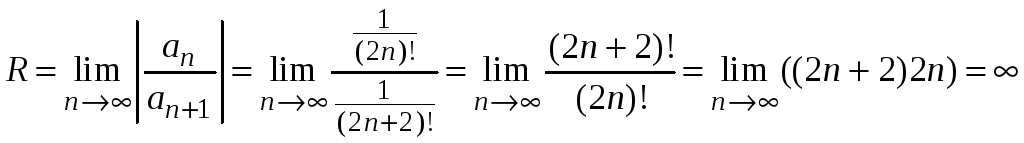 .
.
Область сходимости
ряда
![]() .
.
Пример 9.5. Разложить
в ряд по степеням х
функцию
![]() .
.
Воспользуемся формулой косинуса суммы двух углов, запишем
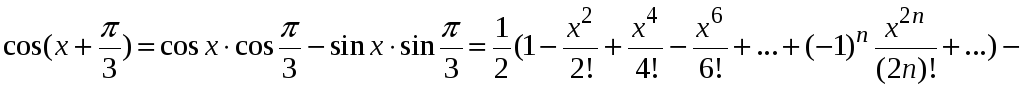
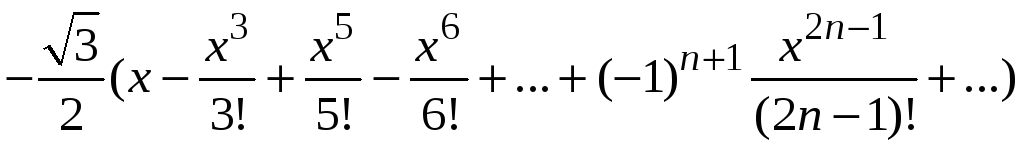 .
.
Пример 9.6. Будем
считать справедливым разложение функции
![]() в ряд Маклорена при мнимом показателе
в ряд Маклорена при мнимом показателе
![]() ,
т. е.
,
т. е.
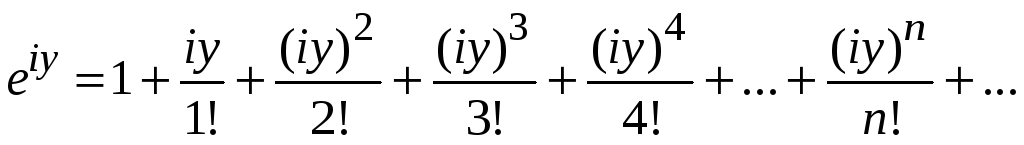 .
.
Здесь
![]()
мнимая единица. Так как
мнимая единица. Так как
![]() и т. д., то
и т. д., то
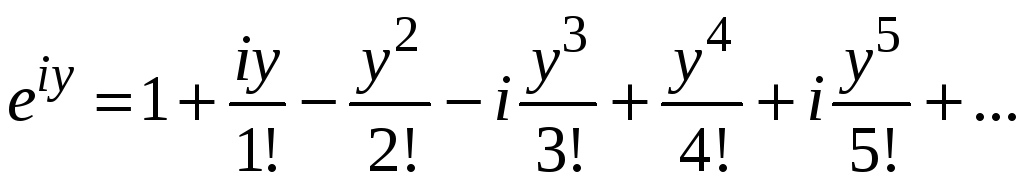 .
.
Сгруппируем действительные и мнимые члены этого ряда, получим
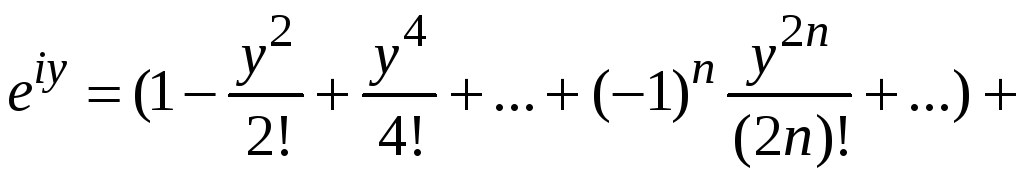
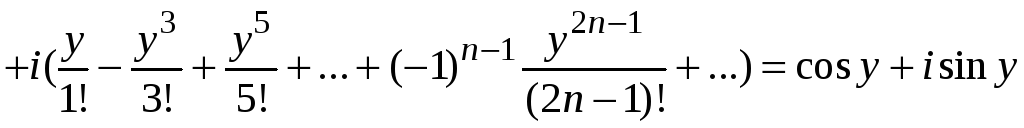 .
.
Отсюда получаем известную формулу Эйлера
![]() .
.
4. Получим разложение
по степеням х
для функции
![]() .
.
Данная функция
удовлетворяет уравнению
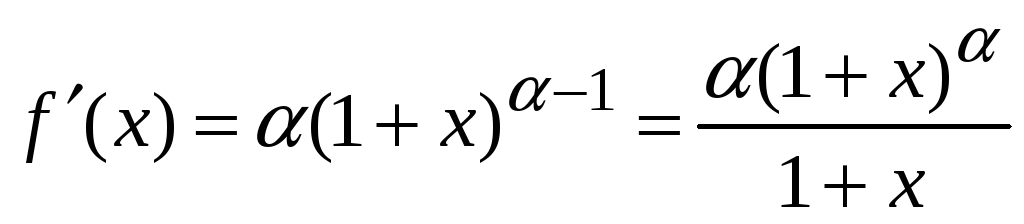 ,
,
т. е.
![]() или
или
![]() .
.
Будем искать
разложение функции
![]() по степеням х
в виде
по степеням х
в виде
![]() .
.
Продифференцируем почленно этот ряд
![]()
и подставим
![]() и
и
![]() в уравнение
в уравнение
![]() ,
получим
,
получим
![]()
![]() .
.
Приравняем
коэффициенты при одинаковых степенях
х
в левой и правой частях этого уравнения;
при этом учтем, что при
![]()
![]() ,
,
т. е.
![]() .
.
При
![]() :
:
![]() ;
;
При
![]() :
:
![]() .
.
При
![]() :
:
![]() .
.
Далее, приравнивая
коэффициенты при
![]() ,
можно получить
,
можно получить
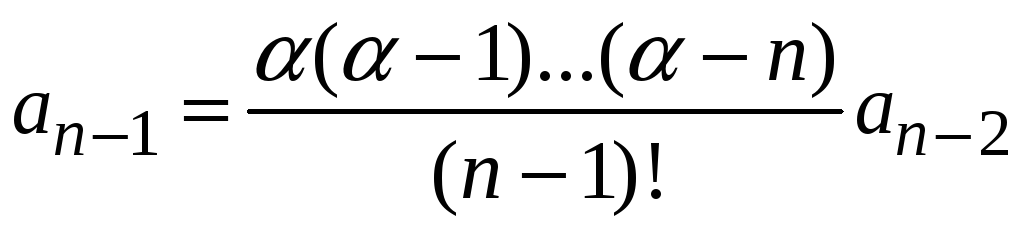 .
Тогда при
.
Тогда при
![]() :
:
![]() .
.
Таким образом,
получаем разложение функции
![]() .
.
![]() .
.
Найдем радиус сходимости этого ряда

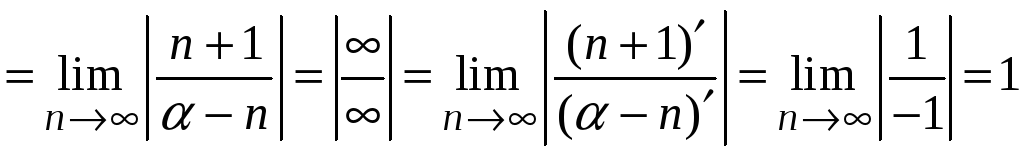 .
.
Интервал сходимости
ряда
![]() .
.
На основании теоремы Вейерштрасса о равномерной сходимости любой степенной ряд в интервале сходимости является равномерно сходящимся. Поэтому ряд составленный из интегралов членов такого ряда сходится к интегралу от суммы этого ряда. Используем это свойство для получения разложений в степенной ряд функций:
![]() и
и
![]() .
.
5. Для функции
![]() можно записать
можно записать
![]() .
.
При
![]() выражение
выражение
![]() можно представить как сумму убывающей
геометрической прогрессии
можно представить как сумму убывающей
геометрической прогрессии
![]() .
.
Так как при
![]() этот ряд (прогрессия) сходится равномерно,
то его можно почленно интегрировать.
Находим
этот ряд (прогрессия) сходится равномерно,
то его можно почленно интегрировать.
Находим
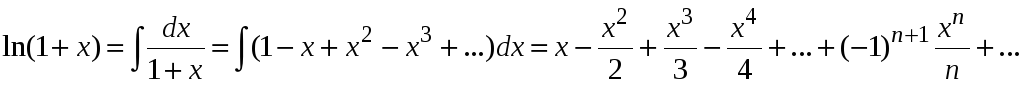 .
.
Следовательно,
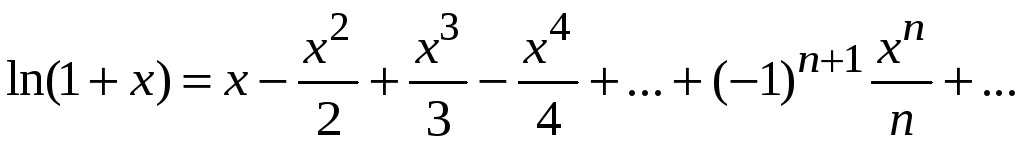 .
.
Найдем радиус сходимости этого ряда.
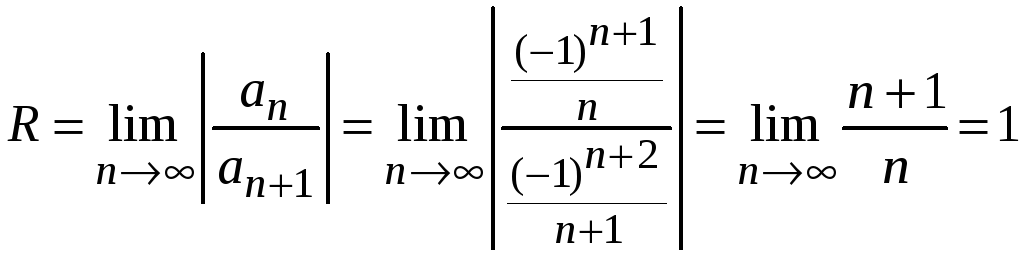 .
.
Интервал сходимости
ряда
![]() .
.
6. Для функции
![]() справедливо равенство
справедливо равенство
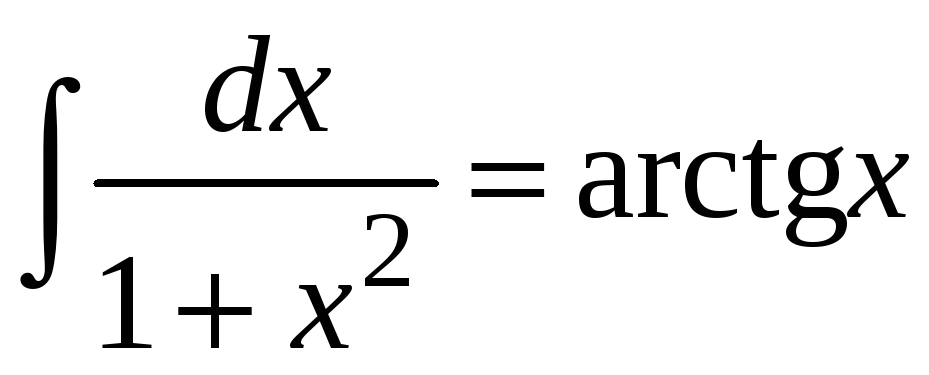 .
.
При
![]() функцию
функцию
 можно представить как сумму убывающей
геометрической прогрессии
можно представить как сумму убывающей
геометрической прогрессии
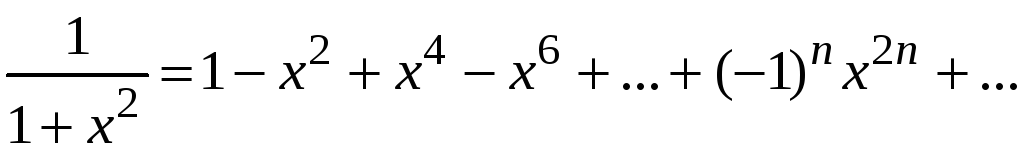 ,
которая сходится равномерно.
,
которая сходится равномерно.
Интегрируя почленно, получим
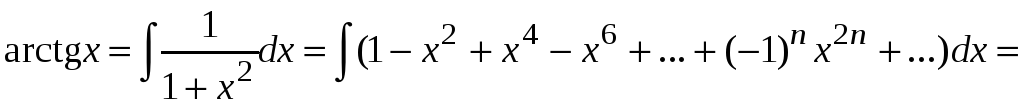
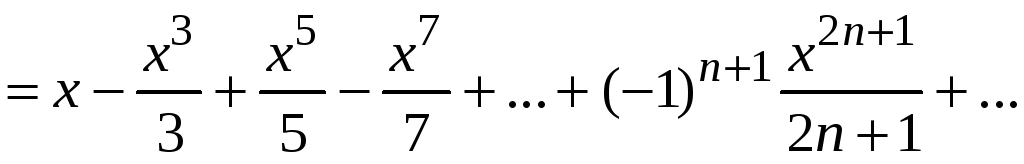 .
.
Следовательно,
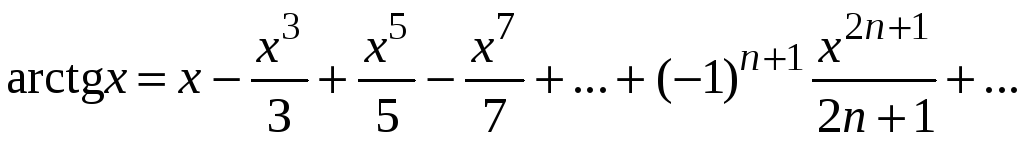 .
.
Радиус сходимости ряда
 .
.
Интервал сходимости
ряда
![]() .
.
7. Для функции
![]() справедливо равенство
справедливо равенство
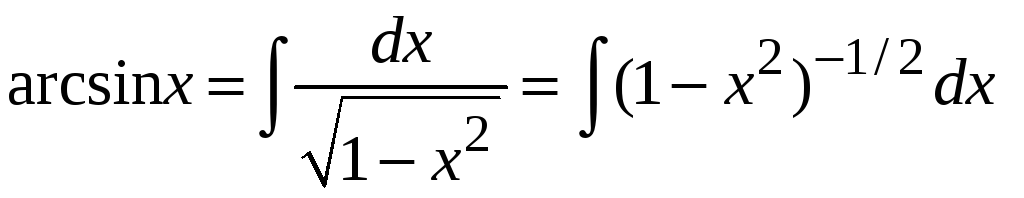 .
.
Запишем разложение биномиального ряда
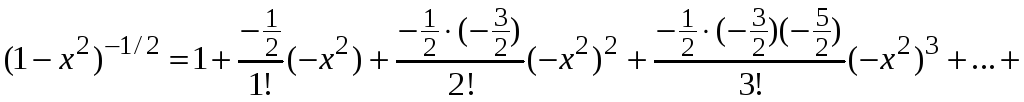

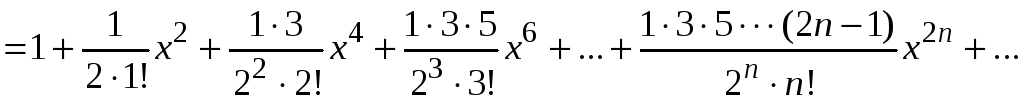 .
.
Данный ряд сходится
равномерно при
![]() .
.
Интегрируем ряд почленно, получим
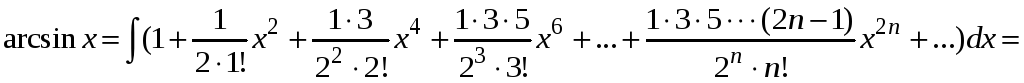

Следовательно,
 .
.
Интервал сходимости
ряда
![]() .
.
