8.4.4. Интегральный признак Коши
Теорема 8.6.
Если члены знакоположительного ряда
,
являющиеся значениями функции
целочисленного аргумента
,
монотонно убывают и стремятся к нулю
,
то: 1) если
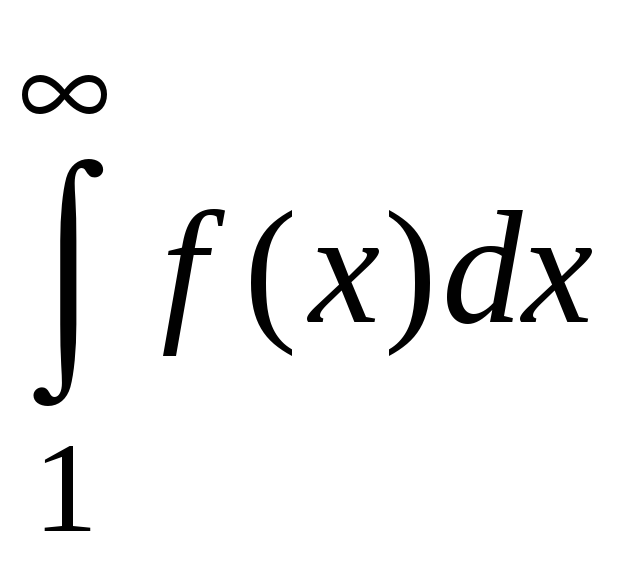сходится, то и ряд
сходится; 2) если
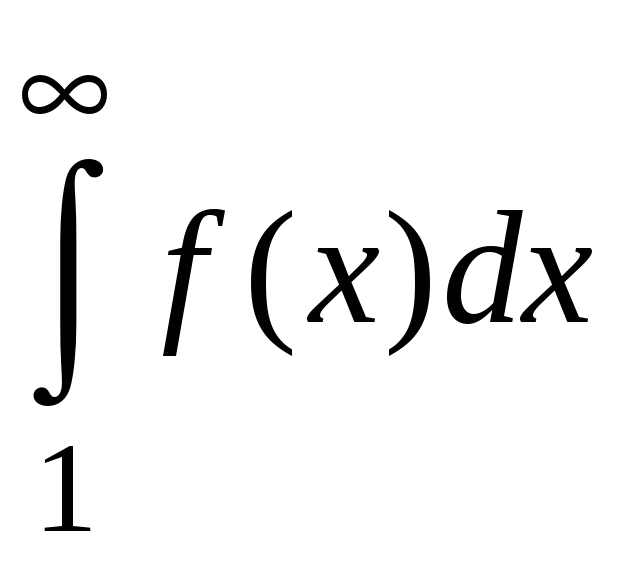расходится, то и ряд
расходится.
Д о к о з а т е л ь
с т в о. В прямоугольной декартовой
системе координат
непрерывная кривая
проходит через точки
и ограничивает сверху криволинейную
трапецию ABCD
(рис. 86). Площадь этой криволинейной
трапеции равняется
.
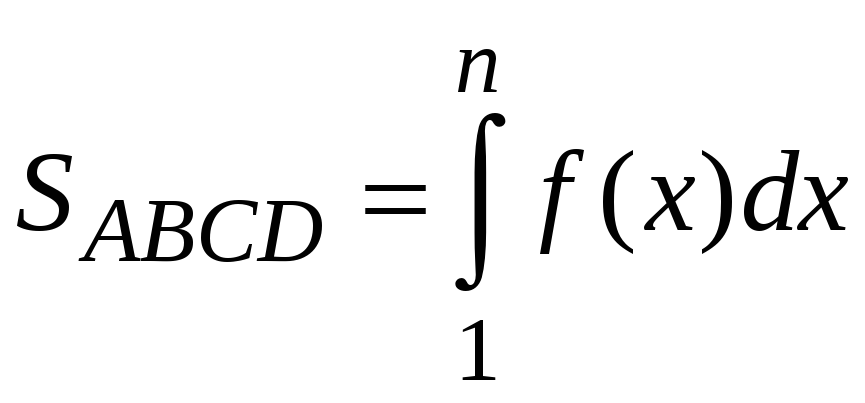Построим две
ступенчатые фигуры с угловыми точками
.
Эти ступенчатые фигуры состоят из
прямоугольников, основания которых
равняются единице, а высоты значениям
.
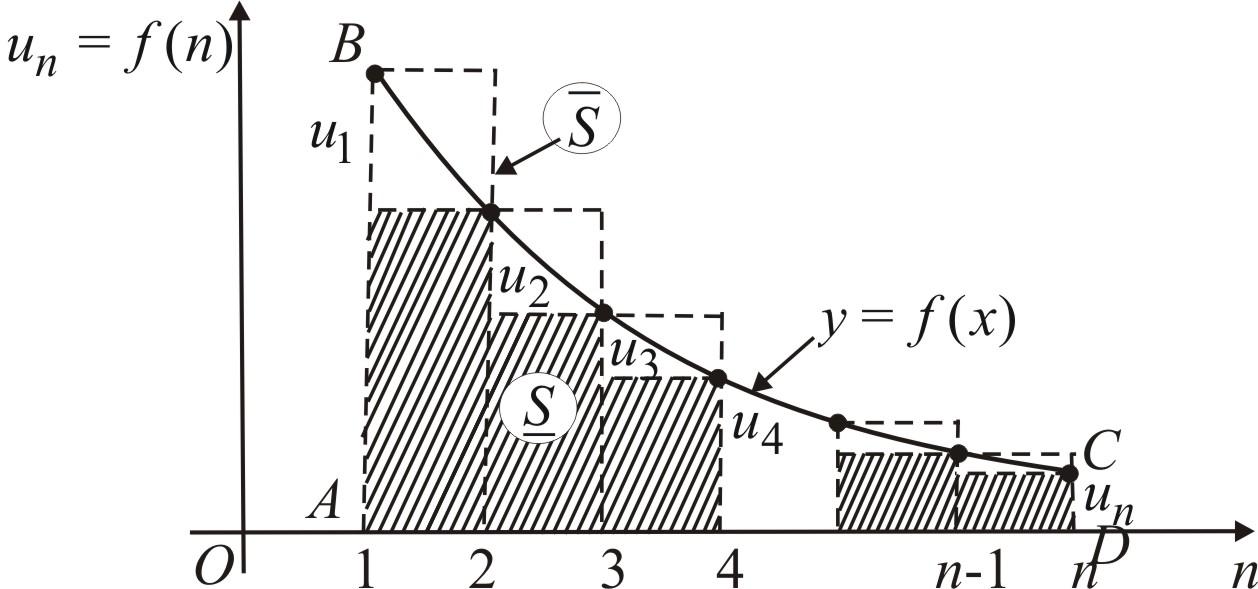
Рис. 86
Найдем площади этих фигур.
,
,
где
n-я
частичная сумма ряда.
Площади этих ступенчатых фигур ограничивают площадь криволинейной трапеции ABCD снизу и сверху
.
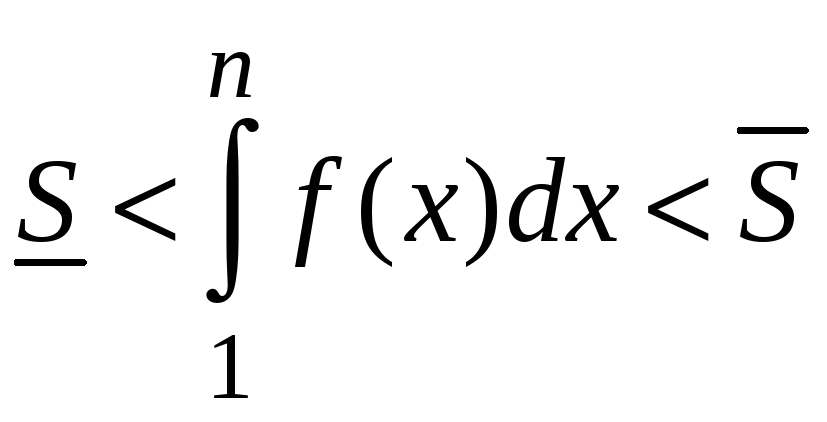
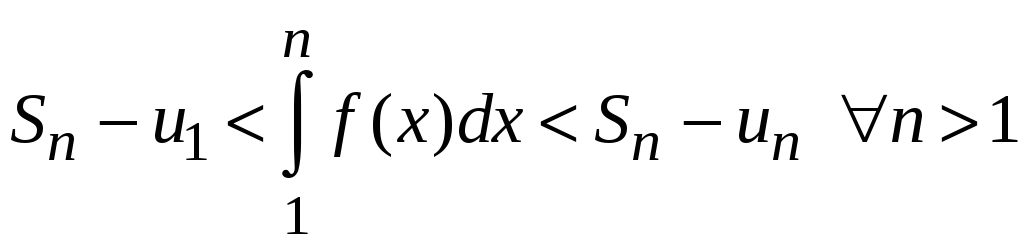Рассмотрим левую часть этого неравенства
.
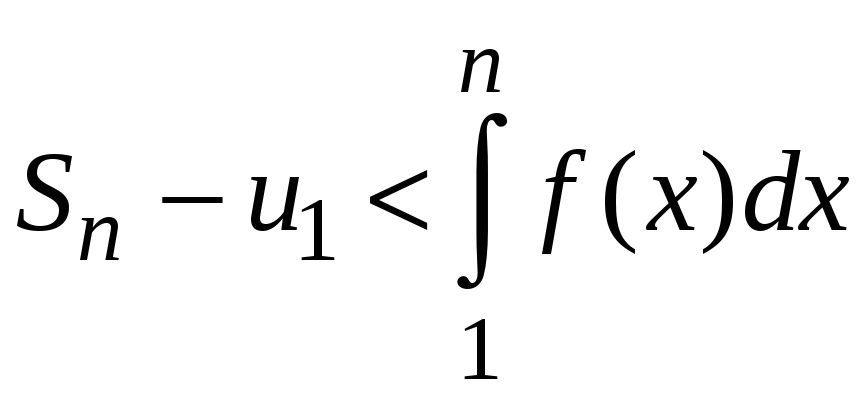
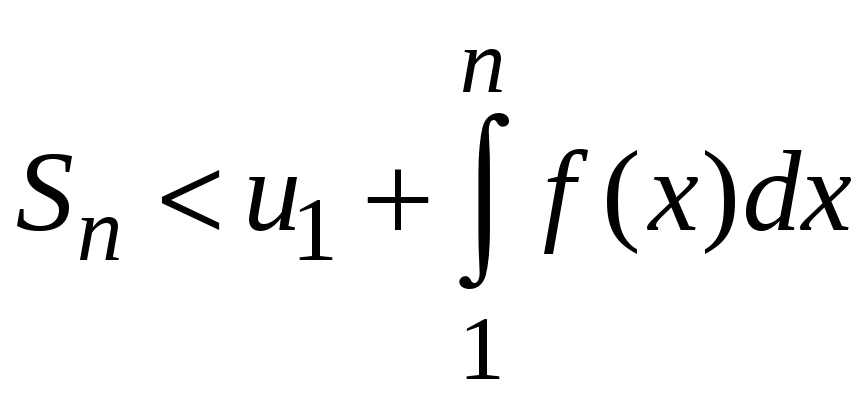При неограниченном
возрастании числа n
членов ряда частичные суммы ряда
монотонно возрастают, так как ряд
знакоположительный. При этом интеграл
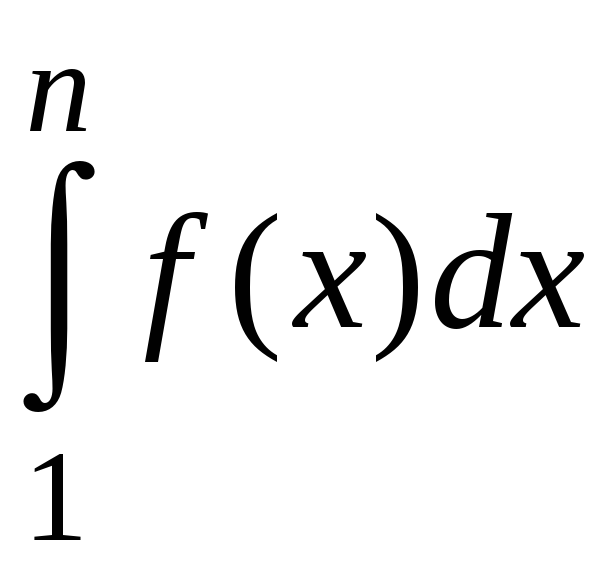также возрастает и ограничен величиной
интеграла
.
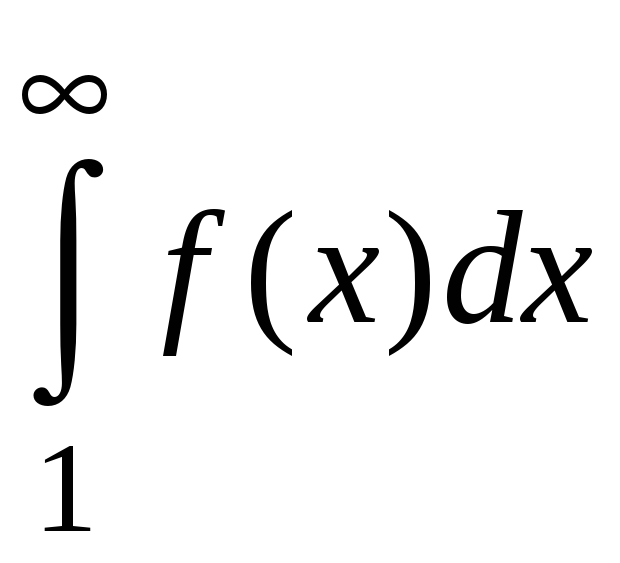Поэтому
,
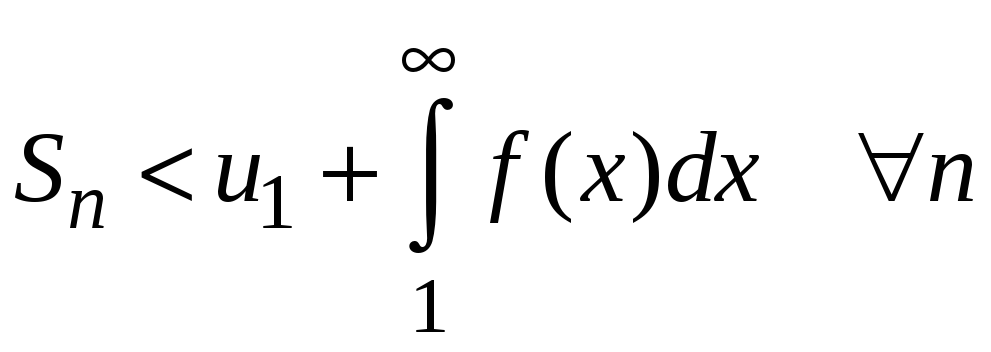т. е. последовательность частичных сумм
ограничена. По теореме Вейерштрасса
существует предел
.
Следовательно, ряд сходится.
Рассмотрим правую часть неравенства
.
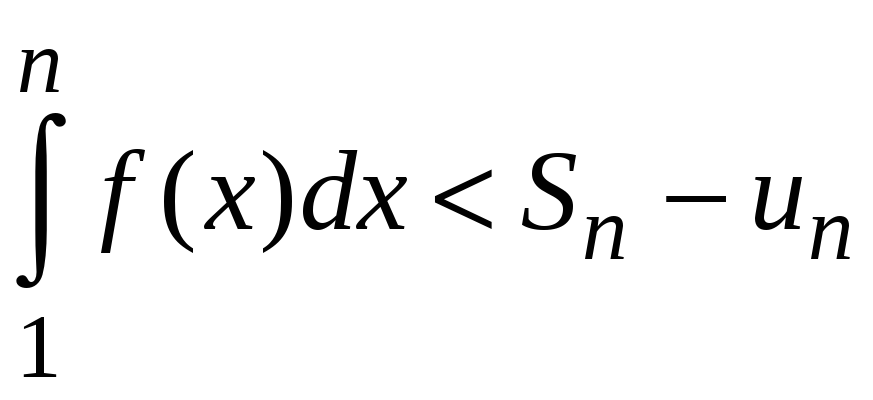
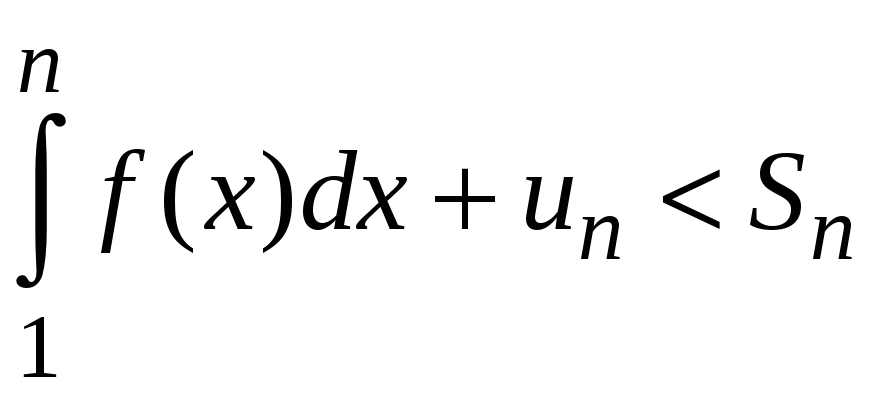По условию теоремы
.
Если
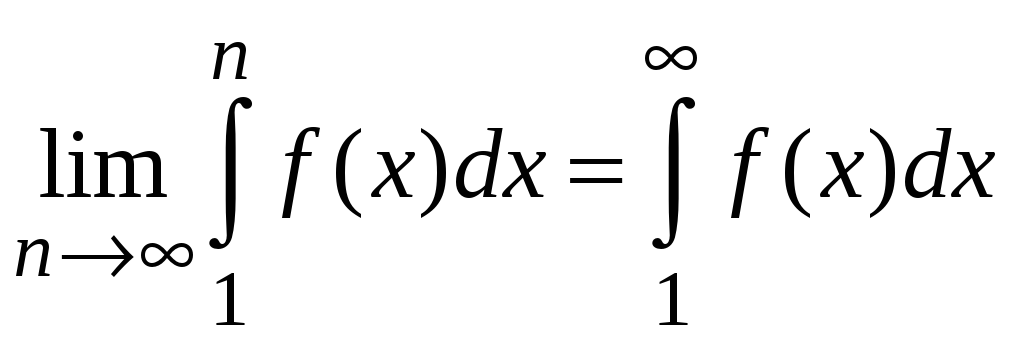неограниченно возрастает, то и предел
частичных сумм
неограниченно возрастает и, следовательно,
ряд расходится.
Таким образом, интегральный признак Коши в принципе позволяет для любого ряда решить вопрос о его сходимости. Трудность в его применении заключается в нахождении несобственных интегралов. Возможности в их нахождении ограниченные.
Пример 8.13.
Исследовать гармонического сходимость
ряда
.
Находим
.
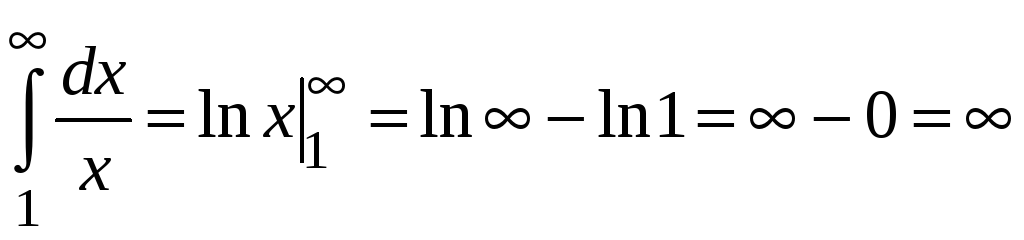Ряд расходится.
Пример 8.14.
Исследовать сходимость обобщенного
гармонического ряда
.
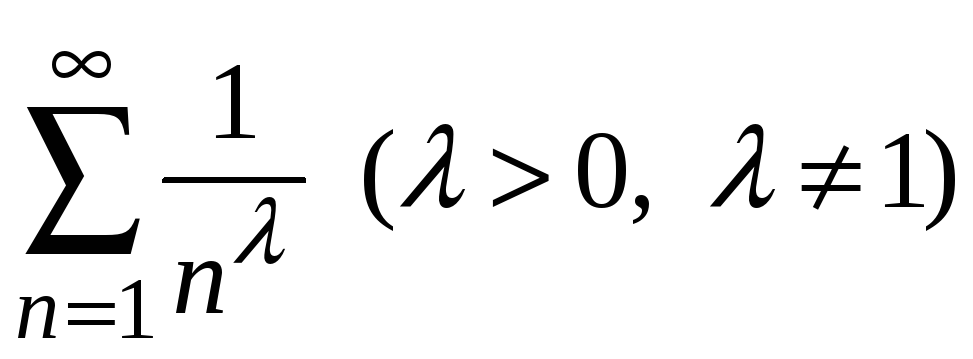Находим
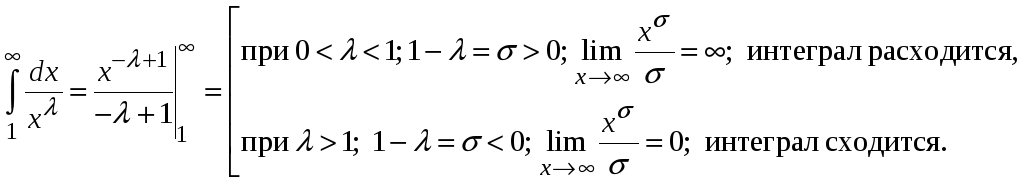
Следовательно,
при
ряд сходится, а при
ряд расходится.
Пример 8.15.
Исследовать сходимость ряда
.
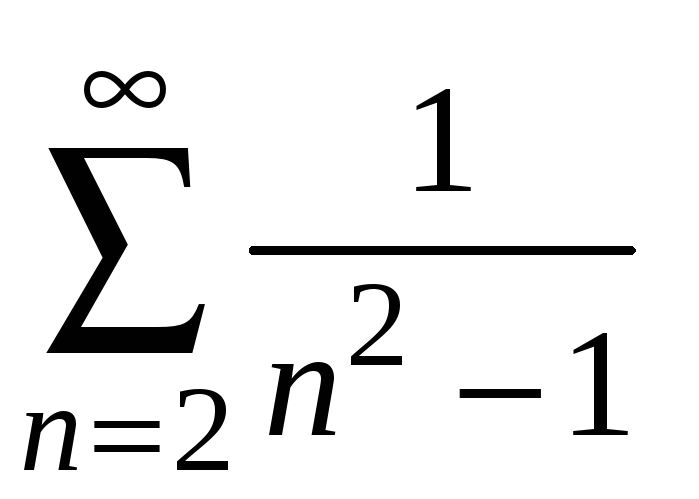Члены ряда нумеруются
с
(при
).
Поэтому при применении интегрального
признака Коши нижний предел интегрирования
равен 2, а не 1. Находим
.
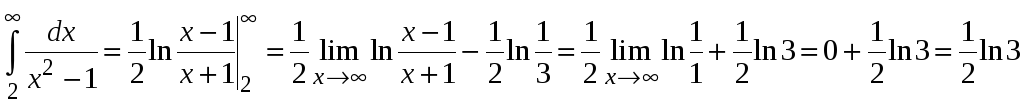Здесь при нахождении предела применили правило Лопиталя. Интеграл сходится, следовательно, и ряд сходится.
Пример 8.16.
Исследовать сходимость ряда
.
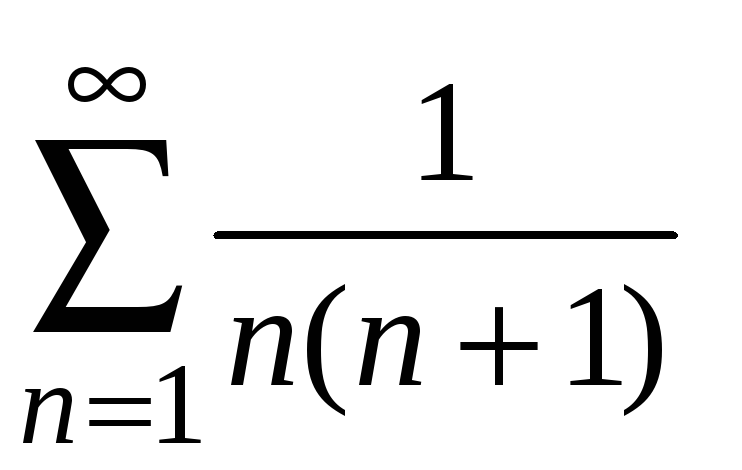Находим
.
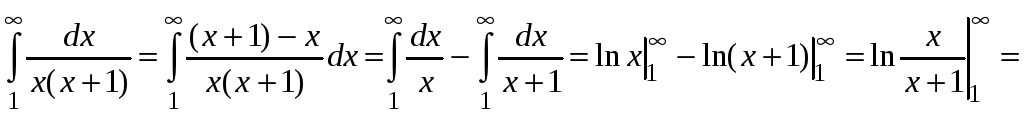
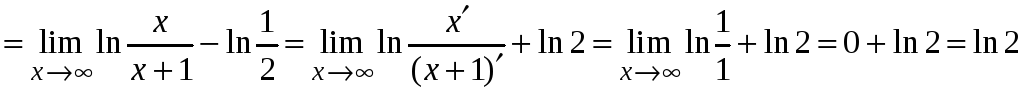Ряд сходится.
8.5. Знакочередующиеся ряды. Теорема Лейбница
Теорема 8.7. Если
члены знакочередующегося ряда
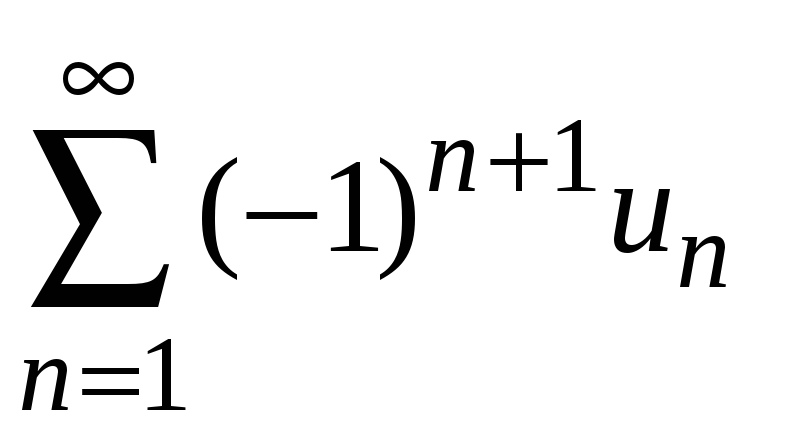монотонно
убывают
и стремятся к нулю
,
то ряд сходится; причем сумма ряда по
абсолютной величине не превосходит
первого члена ряда
.
Д о к а з а т е л ь с т в о. По определению знакочередующегося ряда
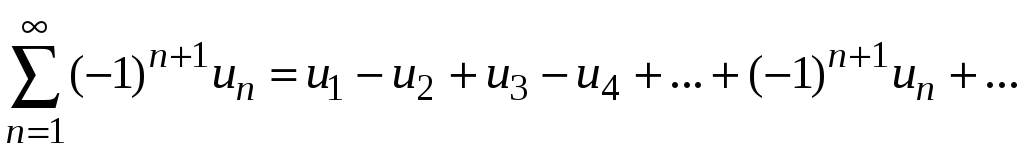
предполагается,
что члены ряда положительные
.
Рассмотрим две
частичные суммы ряда: с четным числом
членов ряда
и с нечетным числом членов
.
В сумме с четным
числом членов
сначала сгруппируем члены попарно
следующим образом
.
Так как члены ряда
монотонно убывают (
),
то разность в каждой скобке суммы
больше нуля и эта сумма монотонно
возрастает с увеличением числа членов
2n.
Теперь сгруппируем члены этой суммы следующим образом
.
Так как в этой
сумме также разность в каждой скобке
больше нуля, то сумма монотонно убывает
с увеличением числа членов 2n
и не превосходит первого члена ряда
.
Следовательно,
последовательность частичных сумм ряда
с четным числом членов монотонно
возрастает и ограничена. Поэтому по
теореме Вейерштрасса она имеет некоторый
предел
.
Найдем также предел частичных сумм ряда с нечетным числом членов.
.
При нечетном числе
членов ряда сумма
также не превосходит первого члена ряда
.
.
Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю.
Частичные суммы знакочередующегося ряда меньше первого члена ряда
.
Члены ряда стремятся к нулю
,
поэтому сумма ряда не может превосходить
первого члена ряда
.
Пример 8.17.
Исследовать сходимость ряда
.
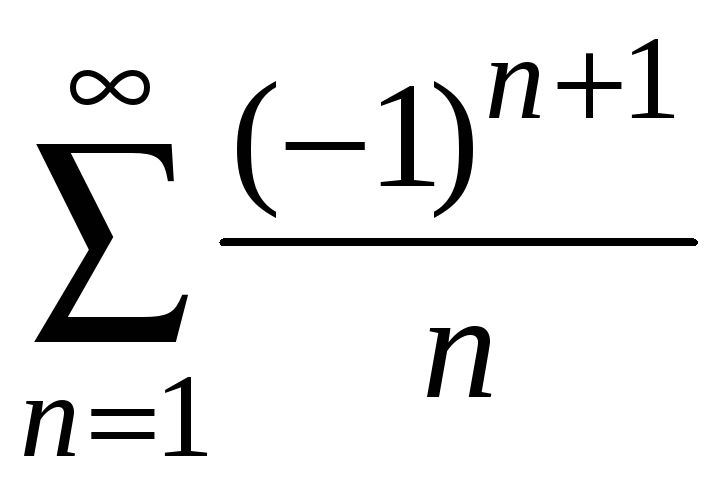Члены ряда монотонно
убывают
и стремятся к нулю
.
Следовательно, ряд сходится.
Пример 8.18.
Исследовать сходимость ряда
.
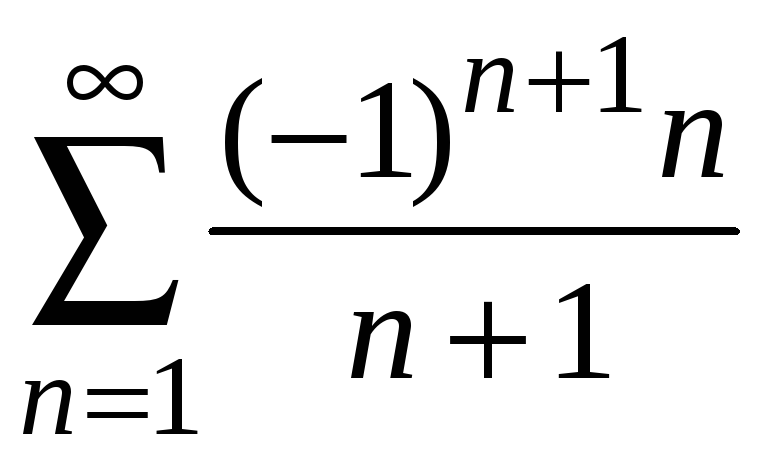Предел членов ряда
при неограниченном возрастании их
номеров отличен от нуля
.
По следствию необходимого признака
сходимости числовых рядов рассматриваемый
ряд расходится.