Методы моделирования объектов автоматического управления

2.3. Укрупнённая методика							2.3. Укрупнена методика
математического моделирования							математичного моделювання ОАК
		ОАУ
На рис. 2.3 представлена графически							На рис. 2.3 графічно зображено
укрупнённая методика			математического				укрупнену	методику		математичного
моделирования ОАУ.							моделювання ОАК.
Начальный		этап	математического				Початковий		етап	математичного
моделирования начинается с формирова-							моделювання починається з формуван-
ния цели и условий, а завершается поста-							ня мети й умов, а завершується поста-
новкой конкретной задачи моделирова-							новкою конкретної задачі моделювання
ния сформированного множества свойств							сформованої	множини		властивостей
ОАУ в желаемой математической форме.							ОАК у бажаній математичній формі.
Следующий этап связан с изучением							Наступний етап пов'язаний з ви-
устройства и принципа действия ОАУ,							вченням будови й принципу дії ОАК,
установлением		физических				законов	визначенням фізичних законів функці-
функционирования ОАУ,					выявлением		онування ОАК,		виявленням вхідних,
входных, выходных сигналов и диапазо-							вихідних сигналів і діапазонів їх змі-
нов их изменения, компонентов ОАУ и							нення, компонентів ОАК і зв'язків.
связей. Этап завершается					построением		Етап завершується побудовою змістов-
содержательной		(вербальной)				модели	ної (вербальної) моделі ОАК.
ОАУ.
Этап	физического			моделирования			Етап фізичного моделювання ОАК
ОАУ состоит в формировании возмож-							полягає у формуванні можливих графі-
ных графических моделей (кинематиче-							чних моделей (кінематичних і функціо-
ских и функциональных схем, статиче-							нальних схем, статичних, динамічних і
ских, динамических и частотных харак-							частотних характеристик), гіпотез і вза-
теристик), гипотез и взаимосвязанной со-							ємозв'язаної сукупності фізичних зако-
вокупности физических законов, отра-							нів, що відображають особливості фун-
жающих особенности функционирования							кціонування ОАК.
ОАУ.
На следующем этапе на основе иде-							На наступному етапі на основі іде-
ализации физическую модель переводят							алізації фізичну модель переводять на
на математический язык описания осо-							математичну мову опису особливостей
бенностей функционирования ОАУ с ис-							функціонування ОАК з використанням
пользованием		соответствующих его					фізичних законів, що відповідають його
свойствам физических законов. Этот пе-							властивостям. Цей перехід базується на
реход базируется на неформальном ана-							неформальному		аналізі	поставленого
лизе поставленной задачи и результатов							завдання й результатів попередніх ета-
предыдущих этапов. При отрицательных							пів. При негативних результатах аналі-
результатах	анализа		после выявления				зу після виявлення причин невідповід-
причин несоответствия ожидаемым ре-							ності очікуваним результатам перехо-
зультатам	переходят		к	корректировке			дять до коригування попередніх етапів.
предыдущих этапов.

71

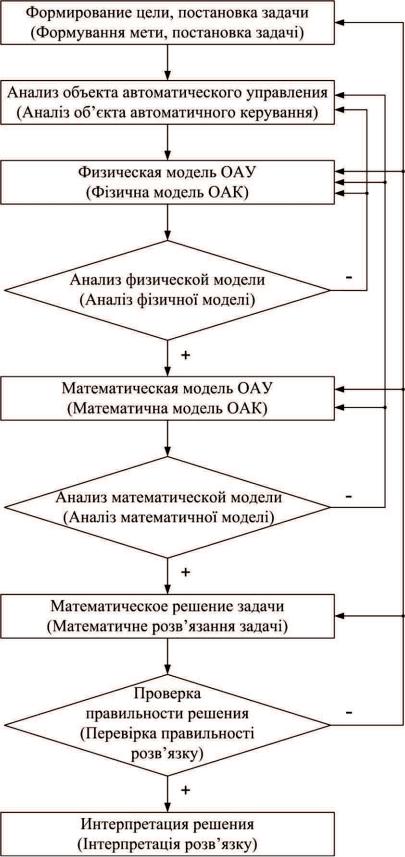
Рис. 2.3. Графическое представление	Рис. 2.3. Графічне зображення
методики математического	методики математичного
моделирования ОАУ	моделювання ОАК
	72

При построении физической модели пренебрегают отдельными несущественными свойствами ОАУ, которые не соответствуют предполагаемому упрощенному математическому описанию, т. е. осуществляют идеализацию ОАУ.

Совокупность математических уравнений, полученных в результате формализации физической модели ОАУ, связывает аналитически выходы y(t) с входными управляющими u(t) и

возмущающими f1(t),...,fn(t) воздействиями. Графически это можно представить в виде схемы (рис. 2.4).

Рис. 2.4. Схематическое изображение вход-выходного описания ОАУ

Математическая модель ОАУ как инструментальное средство исследования включает в себя следующие атрибуты:

1)функционал, критерий и численный показатель адекватности модели;

2)характеристики установившего-

ся устойчивого состояния

u(t0), fi(t0)

иy(t0);

3)диапазоны и характер изменения

входных

воздействий

u(t) U ,

Під час побудови фізичної моделі нехтують окремими несуттєвими властивостями ОАК, що не відповідають очікуваному спрощеному математичному опису, тобто здійснюють ідеалізацію ОАК.

Сукупність математичних рівнянь, отриманих унаслідок формалізації фізичної моделі ОАК, зв'язує аналітично

виходи	y(t) із вхідними керувальними
u(t) і	збурювальними	f1(t),...,fn(t)

впливами. Графічно це можна подати у вигляді схеми (рис. 2.4).

Рис. 2.4. Схематичне зображення вхід-вихідного опису ОАК

Математична модель ОАК як інструментальний засіб дослідження містить такі атрибути:

1)функціонал, критерій і числовий показник адекватності моделі;

2)характеристики усталеного стій-

кого стану

u(t0),fi(t0) і y(t0) ;

3) діапазони і характер змінення вхі-

дних впливів

u(t) U ,

fi(t) Fi ,

fi(t) Fi ,

i =1,n

;

4) диапазон и характер изменения выходных сигналов y(t) Y;

i =1,n

;

4) діапазон і характер змінення вихідних сигналів y(t) Y;

5) математические уравнения, свя-	5)	математичні	рівняння,	що
зывающие выходные и входные пере-	зв’язують вихідні та вхідні змінні;
менные;
6) численные значения коэффици-	6)	числові значення коефіцієнтів рі-

73

ентов уравнений с требуемой точно-						внянь із необхідною точністю;
стью;
7) диапазон и масштаб изменения						7) діапазон і масштаб змінення часу
времени t T,tм = кмt (t				м	− моделиру-	t T,tм	= кмt	(tм	– модельований час,
емое время, км – коэффициент масшта-						км − коефіцієнт масштабу).
ба).
Такая математическая модель поз-						Така математична модель				дасть
волит проводить как вычислительные,						змогу проводити як обчислювальні, так
так и	аналитические			исследования		і аналітичні дослідження властивостей
свойств моделируемого ОАУ, а также						модельованого ОАК, а також вирішу-
решать задачи анализа и синтеза алго-						вати завдання аналізу й синтезу алго-
ритмов функционирования УАУ.						ритмів функціонування ПАК.
Полученную			математическую мо-			Отримана		математична		модель
дель анализируют на предмет суще-						аналізується з огляду на існування ма-
ствования математического решения и						тематичного розв'язку та його однозна-
его однозначности, а также возможных						чність, а також можливі засоби
средств решения математической зада-						розв’язання математичної задачі й точ-
чи и точности возможных решений. Ес-						ність можливих розв’язків. Якщо ця
ли эта модель не позволяет перейти к						модель не дає змоги перейти до насту-
следующему этапу методики, то вносят						пного етапу методики, то вносять від-
соответствующие изменения в преды-						повідні змінення в попередні етапи ме-
дущие этапы методики.						тодики.
На этапе математического решения						На	етапі		математичного
задачи	выбирают		конкретный метод			розв’язання задачі вибирають конкрет-
решения, решают поставленную задачу						ний метод, розв'язують поставлену за-
и оценивают точность полученного ре-						дачу й оцінюють точність отриманого
шения.						розв’язку.
Полученное решение проверяют на						Отриманий розв’язок перевіряють
адекватность, соответствие физическим						на адекватність, відповідність фізичним
ограничениям. При отрицательных ре-						обмеженням. При негативних результа-
зультатах проверки возвращаются на						тах перевірки повертаються на відпові-
соответствующие этапы методики для						дні етапи методики для усунення вияв-
устранения		выявленного			несоответ-	леної невідповідності.
ствия.
Этап интерпретации решения свя-						Етап інтерпретації розв’язку пов'я-
зан с анализом полученных математи-						заний з аналізом отриманих математи-
ческих результатов, установлением со-						чних результатів, визначенням відпові-
ответствия		физическим		характеристи-		дності	фізичним		характеристикам і
кам и свойствам ОАУ, цели и задаче						властивостям ОАК, меті й завданню
математического моделирования ОАУ.						математичного моделювання ОАК.
Каждый ОАУ уникален тем, что в						Кожний ОАК унікальний тим, що
состав его входит, как правило, ориги-						до складу його входить зазвичай оригі-
нальный объект управления специфи-						нальний об'єкт керування специфічної

74

ческой конструкции,		который			имеет	конструкції, який має індивідуальні
индивидуальные принцип				действия,		принцип дії, масо-габаритні й інерційні
массо-габаритные и инерционные ха-						характеристики, конструкцію і склад
рактеристики, конструкцию				и	состав	блока датчикових вимірювачів, розта-
блока датчиковых измерителей, распо-						шування і конструкцію блока виконав-
ложение и конструкцию блока испол-						чих органів з їх інерційними властивос-
нительных органов с их инерционными						тями. На основі поданої укрупненої ме-
свойствами. На основе представленной						тодики формують конкретну методику
укрупнённой	методики		формируют			математичного моделювання, що відо-
конкретную методику математического						бражає цілі й завдання математичного
моделирования,	отражающую				цели и	дослідження реальної гетерогенної під-
задачи математического			исследования			системи.
реальной гетерогенной подсистемы.
При применении конкретной мето-						При застосуванні конкретної мето-
дики моделирования необходимо ис-						дики моделювання необхідно викорис-
пользовать следующие свойства моде-						товувати такі властивості моделей.
лей.
1. Модель представляет собой «че-						1. Модель являє собою «чотиримі-
тырёхместную»	конструкцию,				компо-	сну» конструкцію, компонентами якої є
нентами которой являются субъект, за-						суб'єкт, задача, об'єкт-оригінал і спосіб
дача, объект-оригинал и способ пред-						подання. При цьому задача відіграє
ставления. При этом задача играет роль						роль системотвірного фактора при інте-
системообразующего фактора при ин-						грації відібраних властивостей в єди-
теграции отобранных свойств в единый						ний ідеальний образ як певну
идеальный образ как некоторую це-						цілісність – модель.
лостность − модель.
2. Каждому объекту соответствует						2. Кожному об'єкту відповідає без-
бесчисленное множество различных по						ліч різних по суті моделей. Ця власти-
существу моделей. Это свойство зависит						вість залежить від мети задачі моделю-
от цели задачи моделирования.						вання.
3. Паре «задача − объект-оригинал»						3. Парі «задача – об'єкт-оригінал»
соответствует множество моделей, со-						відповідає безліч моделей, які містять
держащих одну и ту же информацию,						одну й ту саму інформацію, що різ-
различающуюся способами её представ-						ниться способами її подання. Вибір
ления. Выбор	способа		представления			способу подання визначається зручніс-
определяется удобством последующего						тю подальшого використання моделі.
использования модели.
4. Модель − это лишь относитель-						4. Модель – це лише відносна, на-
ное, приближенное подобие объекта-						ближена подібність об'єкта-оригіналу,
оригинала, которое		информационно				що інформаційно є принципово бідні-
принципиально беднее его. Фундамен-						шою за нього. Фундаментальна власти-
тальное свойство: модель беднее объек-						вість: модель є біднішою від об'єкта-
та-оригинала.						оригіналу.
5. Из задачи моделирования следу-						5. Із завдання моделювання випли-

75

ют ограничения и допущения модели. Ограничения касаются исходных свойств, состояний и режимов объекта- оригинала, т. е. входящих в состав модели переменных, параметров и интервалов времени. Допущения определяют примерную степень идеализации свойств реальных объектов и процессов, несущественные факторы фиксируются.

6.Независимо от природы объекта- оригинала и характера задачи модель представляет собой информационное образование.

7.Если объектом моделирования является ранее созданная модель, то в состав вторичной и последующих производных моделей автоматически входят допущения и ограничения, содержащиеся в исходной и промежуточных моделях.

Использование описанных свойств при моделировании ОАУ позволит получить для него эффективные и продуктивные математические модели.

В технологии математического моделирования, схематически представленной на рис. 2.3, есть трудоёмкий, неоднозначный и ответственный переход от этапа формирования физической модели ОАУ к этапу формирования математической конструкции модели ОАУ. Для построения систем математических уравнений традиционно используют различные законы, отражающие физические процессы в ОАУ. При этом полученные системы уравнений в некоторых случаях не полностью отражают динамические свойства ОАУ, что приводит к неадекватности полученных моделей. Более полные и адекватные математические модели можно получить на основе закона сохранения энергии, применяемого в лагранжевом формализме.

вають обмеження й припущення моделі. Обмеження стосуються вихідних властивостей, станів і режимів об'єкта- оригіналу, тобто змінних, параметрів і інтервалів часу, що входять до складу моделі. Допущення визначають приблизну ступінь ідеалізації властивостей реальних об'єктів і процесів, несуттєві фактори фіксуються.

6.Незалежно від природи об'єкта- оригіналу й характеру завдання модель являє собою інформаційне утворення.

7.Якщо об'єктом моделювання є раніше створена модель, то до складу вторинної і подальших похідних моделей автоматично входять допущення й обмеження, що містяться в початковій і проміжних моделях.

Використання описаних властивостей при моделюванні ОАК дасть змогу отримати для нього ефективні й продуктивні математичні моделі.

У технології математичного моделювання, схематично зображеної на рис. 2.3, є трудомісткий, неоднозначний і відповідальний перехід від етапу формування фізичної моделі ОАК до етапу формування математичної конструкції моделі ОАК. Для побудови систем математичних рівнянь традиційно використовують різні закони, що відображають фізичні процеси в ОАК. При цьому отримані системи рівнянь в деяких випадках не повністю відображають динамічні властивості ОАК, що призводить до неадекватності отриманих моделей. Більш повні й адекватні математичні моделі можна отримати на основі закону збереження енергії, що застосовується в лагранжевому формалізмі.

76

2.4. Формирование математической

2.4. Формування математичної

модели с помощью уравнения

моделі з допомогою рівнянь

Лагранжа второго рода

Лагранжа другого роду

Лагранжев формализм − это метод

Лагранжів формалізм – це метод

формирования

уравнений

движения

формування

рівнянь

руху

фізичних

физических объектов с использованием

об'єктів з використанням рівнянь Лаг-

уравнений Лагранжа

второго

рода.

ранжа другого роду. Інші відомі методи

Другие известные методы формирова-

формування рівнянь динаміки руху фі-

ния уравнений динамики движения фи-

зичних об'єктів випливають з відповід-

зических объектов вытекают из соот-

них теорем динаміки. Для багатовимір-

ветствующих

теорем

динамики.

Для

них і багатозв'язних об'єктів викорис-

многомерных и многосвязных объектов

товують такі теореми динаміки: про

используют такие теоремы динамики: о

рух центра мас, про кількість руху, про

движении центра масс, о количестве

момент кількості руху, про кінетичну

движения, о моменте количества дви-

енергію та ін. [1–3]. У лагранжевому

жения, о кинетической энергии и др.

формалізмі

використовуються

тільки

[1−3]. В лагранжевом формализме ис-

теореми про кінетичну й потенціальну

пользуются только теоремы о кинети-

енергії [2, 3].

ческой и потенциальной энергиях [2, 3].

Уравнения Лагранжа второго рода

Рівняння Лагранжа другого роду –

−

это

дифференциальные

уравнения

це диференціальні рівняння руху меха-

движения механического объекта в не-

нічного об'єкта в незалежних узагаль-

зависимых обобщенных координатах.

нених координатах.

Рассмотрим случай свободных ко-

Розглянемо випадок вільних коли-

лебаний

механического объекта. Если

вань механічного об'єкта. Якщо меха-

механическому объекту, находящемуся

нічному об'єкту, що перебуває в стані

в

состоянии

устойчивого

равновесия,

стійкої рівноваги, надають малі відхи-

сообщаются

малые

отклонения

и

лення й початкові швидкості, то об'єкт

начальные скорости, то объект соверша-

здійснює вільні

коливання

відносно

ет

свободные

колебания относительно

положення стійкої рівноваги [4].

положения устойчивого равновесия [4].

Механический объект имеет n сте-

Механічний об'єкт має n ступенів

пеней свободы, и его положение в лю-

свободи, і його положення в будь-який

бой момент времени определяется n

момент часу визначається n узагальне-

обобщенными координатами qi .

ними координатами qi .

В положении устойчивого равнове-

У стані стійкої рівноваги узагаль-

сия обобщенные

координаты

qi0 = 0.

нені координати

qi0 = 0. При

вільних

При свободных колебаниях на механи-

коливаннях на механічний об’єкт діють

ческий объект действуют восстанавли-

відновлювальні сили

Pj і сили опору

вающие силы Pj

и силы сопротивления

R j.

R j.

77

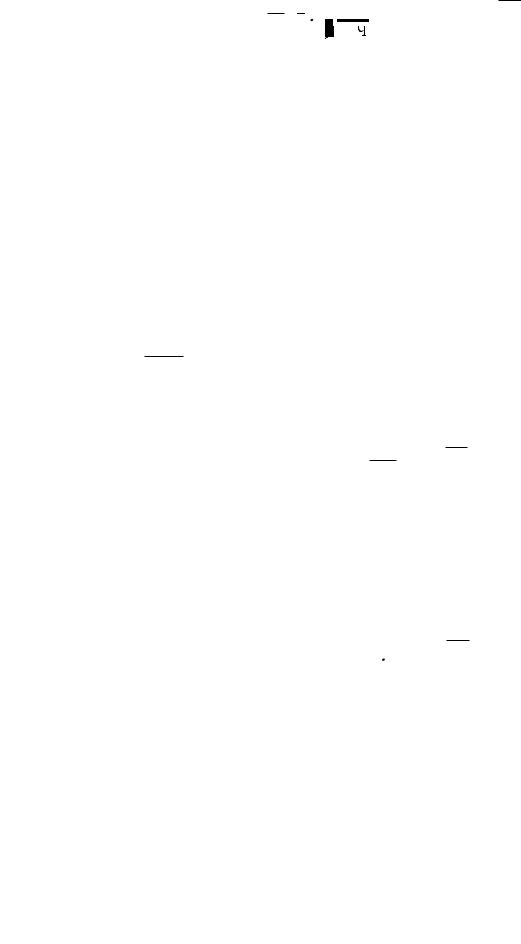
Для объекта с n степенями свободы, совершающего свободные колебания, уравнения Лагранжа второго рода могут быть представлены в таком виде:

Для об’єкта з n ступенями свободи, що здійснює вільні коливання, рівняння Лагранжа другого роду можуть бути подані в такому вигляді:

d ∂T					∂T		P	R
				-					; i =1,n,	(2.1)
dt		∂q			∂q		= Qi	+Qi
			i			i

где Т − кинетическая энергия механи-

де Т − кінетична енергія механічного

ческого объекта;

об’єкта;

P

−

обобщенная сила, соответ-

P

Qi

Qi − узагальнена сила, що відпові-

ствующая

восстанавливающим силам

дає відновлювальним силам P

;

j

Pj;

R

R

−

Qi − узагальнена сила, що відпові-

обобщенная сила, соответ-

дає силам опору R

.

Qi

j

ствующая силам сопротивления R

.

j

Обобщенная сила, по определе-

Узагальнена сила, за означенням, є

нию,

представляет собой

отношение

відношенням елементарної

роботи

элементарной работы δA

qi

к прираще-

δA

qi

до приросту узагальненої коорди-

нию обобщенной координаты

т. е. Qi = δAqi .

δqi

	Известно, что обобщенную
P	определяют по формуле
Qi

δqi ,

силу

	нати δqi , тобто Qi =	δAqi	.
		δqi

Відомо, що узагальнену силу визначають за формулою

Q

P i

		P		∂П
	Q		= -	;	i =1,n,
		i
				∂q
				i

(2.2)

где П − потенциальная энергия механи-	де П − потенціальна енергія механічно-
ческого объекта.	го об’єкта.
Обобщенную силу QiR можно	Узагальнену силу QiR можна ви-
определить через диссипативную	значити через дисипативну функцію
функцию Рэлея Ф согласно следующей	Релея Ф згідно з такою формулою:
формуле:

	Q	R	= -	∂ Ф	i =1,n.
				;
		i
				∂q
				i

(2.3)

Диссипативная функция Ф, или функция рассеивания, связана с кинетической и потенциальной энергиями таким соотношением:

Дисипативна функція Ф, або функція розсіювання, зв’язана з кінетичною й потенціальною енергіями таким співвідношенням:

	d(T + П)	= - 2Ф.	(2.4)
	dt
Рассмотрим общий случай вынуж-		Розглянемо загальний випадок ви-

78

денного движения механического объекта с одной степенью свободы вблизи положения устойчивого равновесия, когда действуют восстанавливающие силы Pj, силы сопротивления R jи воз-

мущающие силы F	. Возмущающие си-
j

лы вызывают вынужденные колебания объекта.

Предполагаем, что восстанавлива-

ющие силы		P	j	имеют потенциал, силы
сопротивления				R	j	пропорциональны
скорости υ	j	, а возмущающие силы F
						j
заданы как		Fj		= Fj(t). Тогда кинетиче-

ская энергия Т, потенциальная энергия П и функция рассеивания Ф определяются следующими выражениями:

мушеного руху механічного об'єкта з одним ступенем свободи поблизу положення стійкої рівноваги, коли діють відновлювальні сили Pj, сили опору R j

і збурювальні сили Fj . Збурювальні си-

ли спричиняють вимушені коливання об'єкта.

Припускаємо, що			відновлювальні
сили P	j	мають потенціал, сили опору
R j є пропорційними швидкості υj					, а
збурювальні сили			F	задано	як
			j

Fj = Fj(t). Тоді кінетична енергія Т, по-

тенціальна енергія П і функція розсіювання Ф визначаються такими виразами:

1 T =

2

2

q

П =

сq

2

;

Ф =

bq

2

,

(2.5)

где a − коэффициент инерции; с − коэффициент жёсткости;

b − коэффициент диссипации.

Обобщённые силы Q	P	и Q	R	, кото-

рые соответствуют восстанавливающим

силам

Pj

и силам сопротивления

R j

,

вычислим с помощью следующих формул:

		P			∂П
	Q		= -		= -cq;
					∂q
Обобщенная сила	Q		F	,	соответ-
ствующая возмущающим				силам		F ,
							j
определяется формулой
					m		∂xj
QF(t) = ∑ Fjx

j=1 ∂q

де a − коефіцієнт інерції;

с − коефіцієнт жорсткості; b − коефіцієнт дисипації.

Узагальнені

сили

Q

P

і Q

R

, що

відповідають відновлювальним

силам

Pj

і силам опору

R j, обчислюємо з до-

помогою таких формул:

Q

R

= -

∂Ф

(2.6)

= -bq

∂q

Узагальнена сила

Q

F

, яка відпові-

дає збурювальним силам

F , визнача-

j

ється формулою

∂yj

∂zj

+ Fjy

+ Fjz

.

(2.7)

∂q

∂q

Уравнение Лагранжа для рассматриваемого механического объекта будет иметь вид

Рівняння Лагранжа для механічного об’єкта, що розглядається, матиме вигляд

d	∂Τ	-	∂Τ	(2.8)
	∂q		= QP + QR + QF(t).
dt			q
			79

Выполнив соответствующие дей-	Здійснивши відповідні дії і підста-
ствия и подстановки, получим выраже-	новки, отримаємо вираз
ние

aq + bq +cq

=

Q

F

(t).

Разделив обе части уравнения на коэффициент a, получим дифференциальное уравнение вида

Поділивши обидві частини рівняння на коефіцієнт a, отримаємо диференціальне рівняння вигляду

	2	1	F
	q + 2nq + k q =	Q		(t),	(2.9)
		a

		b			2	c
	где	2n =	и	k		= .
		a				a

Уравнение (2.9) является общим дифференциальным уравнением вынужденных колебаний механического объекта с одной степенью свободы, которое отражает преобразовательные свойства этого объекта.

Математическое решение задачи в соответствии со схемой, изображенной на рис. 2.3, заключается в нахождении решения дифференциального уравнения (2.9). Решение линейного дифференциального уравнения с постоянными коэффициентами, а таким является уравнение (2.9), состоит из общего и частного решений.

Общее решение дифференциального уравнения (2.9) зависит от решения соответствующего однородного уравнения

		b			2	c
	де	2n =	i	k		= .
		a				a

Рівняння (2.9) є загальним диференціальним рівнянням вимушених коливань механічного об'єкта з одним ступенем свободи, що відображає перетворювальні властивості цього об'єкта.

Математичне розв’язання задачі відповідно до схеми, зображеної на рис. 2.3, полягає в знаходженні розв’язку диференціального рівняння (2.9). Розв’язок лінійного диференціального рівняння з постійними коефіцієнтами, а таким є рівняння (2.9), складається із загального і частинного розв’язків.

Загальний розв’язок диференціального рівняння (2.9) залежить від розв’язку відповідного однородного рівняння

q + 2nq + kq = 0.

(2.10)

Если n < тивления), то

k

(случай малого сопро-

Якщо ру), то

n < k

(випадок малого опо-

q = e	-nt	(C cos	k	2	- n	2	t + C sin	k	2	- n	2	t).
		1					2

(2.11)

Постоянные	интегрирования	Постійні інтегрування
C1 и C2 находят из начальных условий:		ходять із початкових умов:

С (0) = q	0	;	С	2	=	q0		+ nq0		.
1							k2 + n2
Тогда							Тоді
q(0) = q0;					q(0) = q0

C	i
1

C

2

зна-

(2.12)

80