Линейные операторы

Основная статья: Линейное отображение

Оператор L (действующий из векторного пространства в векторное же) называется линейным однородным (или просто линейным), если он обладает следующими свойствами:

1. может применяться почленно к сумме аргументов:

L(x₁ + x₂) = L(x₁) + L(x₂);

2. скаляр (постоянную величину) c можно выносить за знак оператора:

L(cx) = cL(x);

Из 2) следует, что для линейного однородного оператора справедливо свойство L(0) = 0.

Оператор L называется линейным неоднородным, если он состоит из линейного однородного оператора с прибавлением некоторого фиксированного элемента:

L{x} = L₀{x} + φ,

где L₀ — линейный однородный оператор.

В случае линейного преобразования дискретных функций (последовательностей, векторов) новые значения функций y_k являются линейными функциями от старых значений x_k:

.

В более общем случае непрерывных функций двумерная матрица весов принимает вид функции двух переменных , и называется ядром линейного интегрального преобразования:

Функция-операнд f(ω) в данном случае называется спектральной функцией. Спектр может быть и дискретным, тогда f(ω) заменяется вектором W. В этом случае φ(t) представимо конечным или бесконечным рядом функций:

[Править] Единичный (тождественный) оператор

Оператор E, ставящий в соответствие каждому вектору сам вектор , очевидно, линейный; он называется единичным или тождественным оператором.

Частный случай линейного оператора, возвращающий операнд в неизменном виде:

то есть как матричный оператор определяется равенством

и как интегральный оператор — равенством

.

Единичная матрица E_ik записывается большей частью с помощью символа δ_ik = δ_ki (символ Кронекера). Имеем: δ_ik = 1 при i = k и δ_ik = 0 при .

Единичное ядро E(x,t) записывается в виде E(x,t) = δ(t − x) (дельта-функция). δ(x − t) = 0 всюду, кроме x = t, где функция становится бесконечной и притом такой, что

.

• Образом подмножества^[1] относительно линейного отображения A называется множество .

• Ядром линейного отображения называются подмножество A, которое отображается в нуль:

Ядро линейного отображения образует подпространство в линейном пространстве A.

• Образом линейного отображения f называется следующее подмножество B:

Образ линейного отображения образует подпространство в линейном пространстве B.

• Отображение 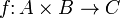прямого произведения линейных пространств A и B в линейное пространство C называется билинейным, если оно линейно по обоим своим аргументам. Отображение прямого произведения большего числа линейных пространств называется полилинейным, если оно линейно по всем своим аргументам.

• Оператор называется линейным неоднородным (или афинным), если он имеет вид

где L — линейный оператор, а v — вектор.

• Пусть . Подпространство называется инвариантным относительно линейного отображения, если ^[2].

Критерий инвариантности. Пусть — подпространство,такое что X разлагается в прямую сумму: . Тогда M инвариантно относительно линейного отображения A тогда и только тогда, когда P_MAP_M = AP_M, где P_M - проектор на подпространство M.

Образ и ядро линейного оператора

Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X. Доказано, что образ Im(A) линейного оператора линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается  Rg(A) = r = dim( Im(A) ).

Ядром линейного оператора называется множество элементов из X, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A) :  Ker(A) = {x e X : A(X) =0 } . Ядро линейного оператора линейное пространство; размерность ядра линейного оператора называется дефектом оператора, обозначается Def(A):   d = Def(A) = dim ( Ker(A) ) .

Для линейного оператора, действующего в n-мерном линейном пространстве X, справедливы следующие утверждения:

сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор:

Def(A) + Rg(A) = n; 

ранг оператора равен рангу его матрицы;

ядро оператора совпадает с множеством  решений линейной однородной системы с матрицей A, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.

50/B