Матрица перехода

Понедельник, 9 ноября 2009 г. Рубрика: Матрица перехода и ее свойства Просмотров: 5026

Пусть ,  – два базиса произвольного векторного пространства V над полем K. Назовем первый базис "старым", а второй "новым". Разложим векторы нового базиса по старому базису:

                          (2)

(Обратите внимание на нумерацию коэффициентов!)

Каждое равенство в (2) можно записать в матричной форме, если мы формально воспользуемся правилом умножения строки на столбец. Пусть  – строка длины , элементами которой являются векторы старого базиса. Аналогично,  – вектор–строка нового базиса. Будем рассматривать эти строки как матрицы соответствующих размеров и производить с ними действия как с числовыми матрицами. (Такие действия можно обосновать.) Тогда, ,

.

Если мы обозначим столбец координат вектора  через :

,

то последнее равенство можно записать в виде:

,

а всю систему равенств (2) – в виде:

,

где

.

Таким образом, равенства (2) в матричной форме записи имеют вид:

.         (3)

Такая форма записи позволяет значительно облегчить выкладки.

Определение. Матрица

называется матрицей перехода от старого базиса  к новому базису .

Матрицу перехода от базиса  к базису  мы обозначать буквой С или  или .

В этих обозначениях равенство (3) принимает вид:

                         (4)

42/B

Неоднородной системой линейных уравнений называется система вида:

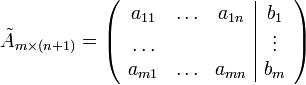— её расширенная матрица.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

43/B

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.

Обычно ранг матрицы A обозначается ( ) или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.