Свойства Геометрические свойства

• Модуль каждого корня равен 1. На комплексной плоскости корни из единицы образуют вершины правильного многоугольника, вписанного в единичную окружность. Одной из вершин всегда является комплексная единица.

• Если u_k — корень из единицы, то сопряжённое к нему число  — тоже корень из единицы.

• Пусть M — произвольная точка единичной окружности. Тогда сумма квадратов расстояний от M до всех корней из единицы равна 2n.

Алгебраические свойства

• Корни из единицы представляют собой целые алгебраические числа.

• Корни из единицы образуют по умножению группу. Обратный элемент для каждого элемента этой группы совпадает с сопряжённым ему. В частности, любая целая степень корня из единицы тоже является корнем из единицы.

• Группа корней из единицы изоморфна аддитивной группе классов вычетов . Отсюда следует, что она является циклической группой; в качестве порождающего (первообразного) можно взять любой элемент u_k, индекс k которого взаимно прост с n.

  • Следствия:

  • элемент u₁ всегда является первообразным;

  • если n — простое число, то степени любого корня, кроме , охватывают всю группу;

  • число первообразных корней равно 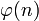, где — функция Эйлера.

• Если n > 1, то для суммы степеней любого первообразного корня из единицы u имеет место формула:

• 

Примеры

Кубические корни из единицы

Кубические корни из единицы:

Корни 4-й степени из единицы:

Для корня 5-й степени имеются 4 порождающих элемента:

Для корня 6-й степени порождающих элементов только два:

37.BМногомерное пространство являются n-мерные евклидовы пространства, где n может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, «точка» n-мерного евклидова пространства задаётся n «координатами» x₁, x₂, ..., x_n (которые могут принимать любые действительные значения); расстояние r между двумя точками M(x₁, x₂, ..., x_n) и М"(у₁, y₂, ..., y_n) определяется формулой аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n-мерного пространства и другие геометрические понятия. Так, в Многомерное пространство рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < n), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений).   Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия n-мерного евклидова пространства.

Линейная комбинация векторов

     Линейной комбинацией векторов называют вектор

     

где - коэффициенты линейной комбинации. Если комбинация называется тривиальной, если - нетривиальной.

     Линейная зависимость и независимость векторов

     Система линейно зависима что

     Система линейно независима

     Критерий линейной зависимости векторов

     Для того чтобы векторы (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

     Размерность линейного пространства

     Линейное пространство V называется n-мерным (имеет размерность n), если в нем:

     1) существует n линейно независимых векторов;

     2) любая система n + 1 векторов линейно зависима.

     Обозначения : n = dim V; .