Системы обыкновенных дифференциальных уравнений
Дано к-уравнений:
(1)
Видим, что система (1) связывает независимые
переменные x и k
искомых функций, причем в уравнениях
искомые функции входят также в качестве
производных соответствующего порядка,
требуется определить функцию
,
удовлетворяющую системе (1). Будем
предполагать, что число уравнений равно
числу неизвестных функций и что система
(1) решаема относительно старших
производных. При сделанных оговорках
можно представить в виде:
(2)
(2) называется канонической.
Систему из к уравнений можно заменить
эквивалентной системой из n-уравнений,
где
первого порядка, разрешенных относительно
производных, для этого вводят новую
систему функций.
…
…
…
…
(3)
Система (3) отвлекает от разделение на группы, пронумеровав все функции в виде одного простого ряда, можно записать в общем случае в виде:
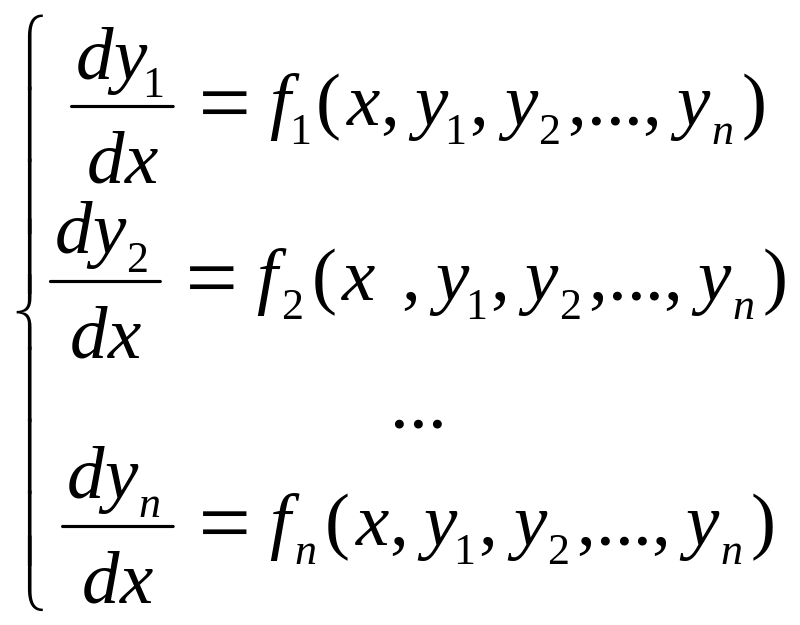(4)
Составили систему(4) названную системой, имеющую нормальную форму Коши.
Дифференциальные уравнения 1-го порядка
Уравнение 1-го порядка можно заменить
системой:
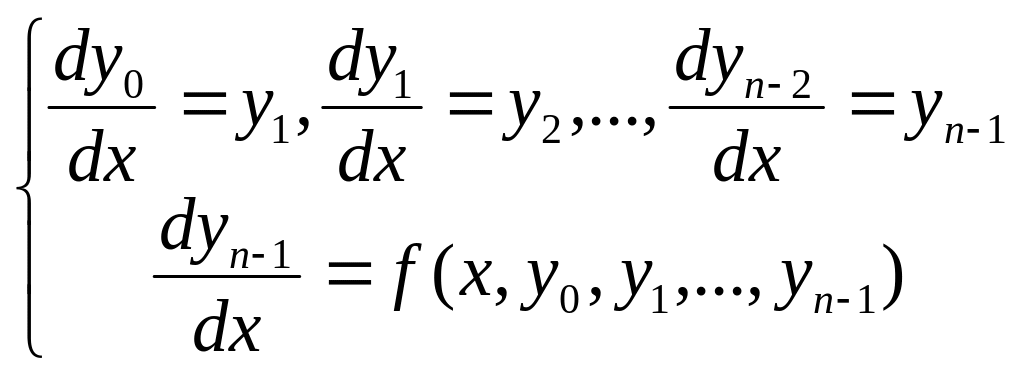
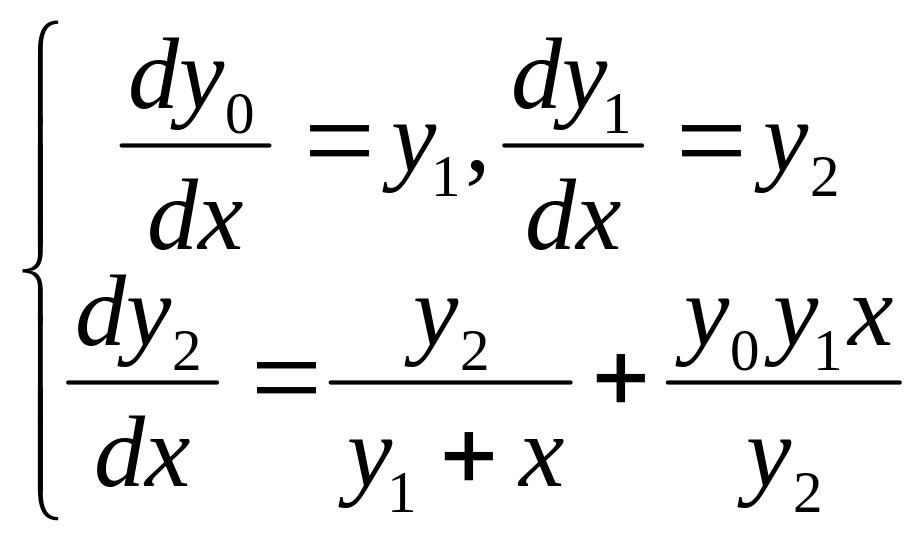
Справедливо и обратное утверждение:
Нормированная система n уравнений первого порядка эквивалентна одному уравнению порядка n.
Случай системы (2). Уравнение n-го порядка можно заменить системой:
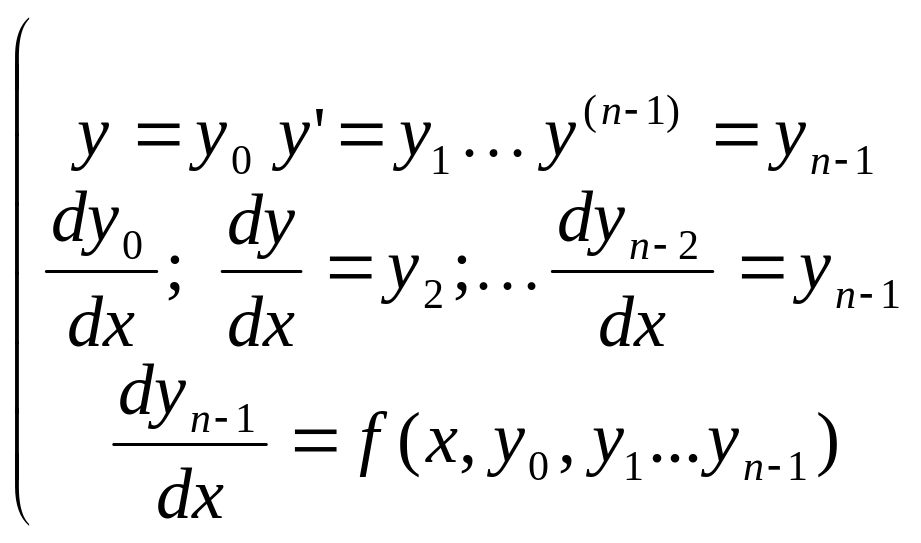
Пример:
Уравнение 3-го порядка:
Справедливо и обратное утверждение:
Нормальная система n уравнений 1-го порядка эквивалентна одному уравнению порядка n
Дифференцируем первое из уравнений (4) по x
Заменим
через их выражение
Получим выражение вида:
Полученное уравнение снова дифференцируем по x, принимая во внимание (4), получим.
Или
Продолжая этот же процесс, получим далее:
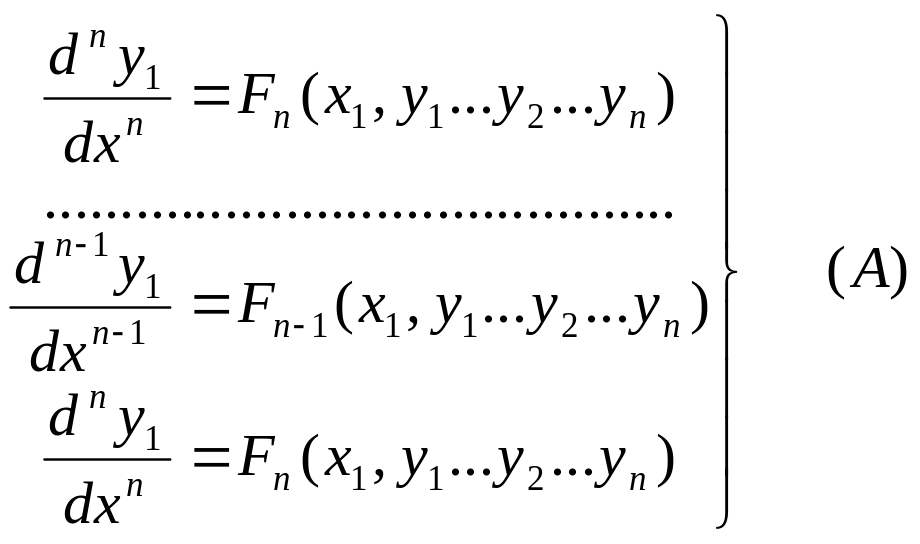
Из системы А из первого уравнения системы
(4), (4’),(4’’) можно определить n-1
величину
через
Внося это выражение в последнее уравнение системы (А), получим уравнение вида:
Т.е. одно уравнение первого порядка.
Пример: Привести следующую систему к одному уравнению высшего порядка и найти их общее решение:
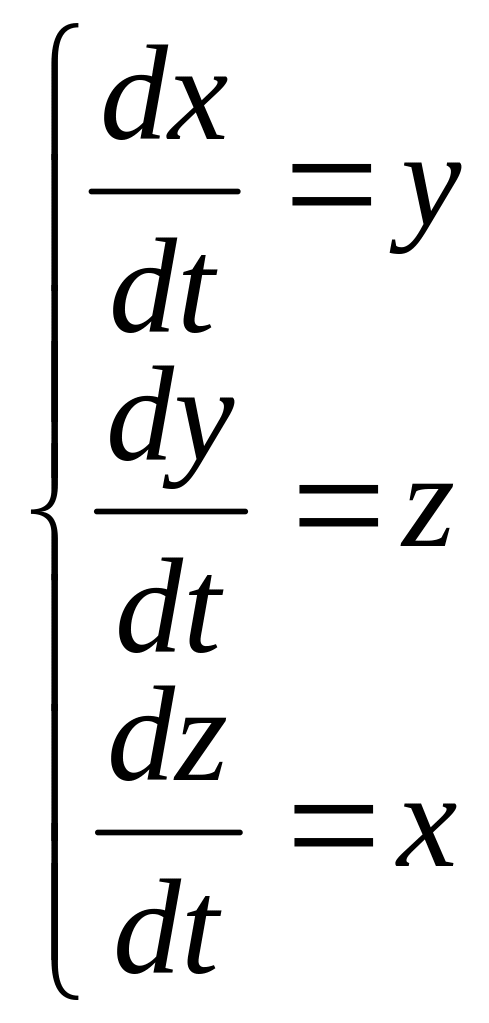
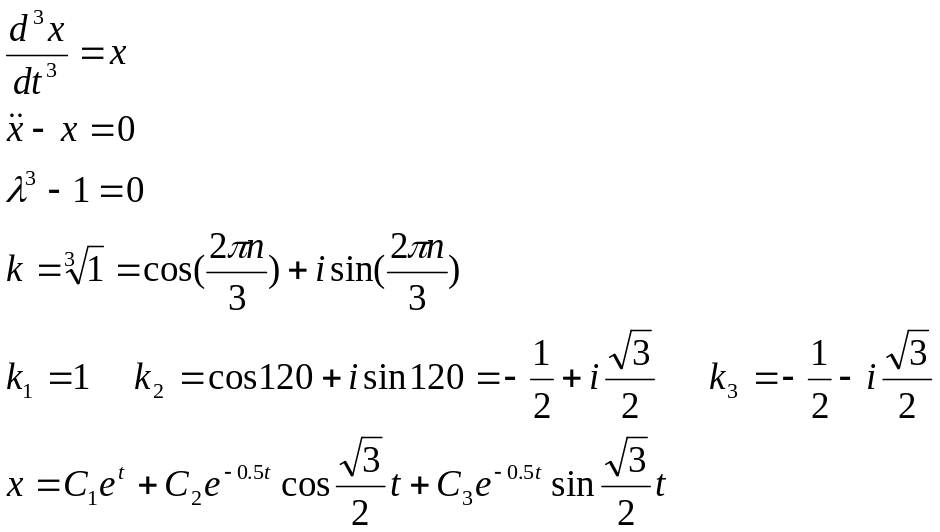
Геометрический смысл системы уравнений первого порядка
Рассмотрим случай системы из 2-уравнений
первого порядка с двумя неизвестными
функция
Если эту систему удастся решить
относительно
то она принимает нормальную форму:
Решением системы (1),(1”) называется пара
функций
(2)
обращающая оба уравнения в тождества,
поскольку система (1’) равносильна
одному уравнению второго порядка , то
общее решение системы содержит 2
постоянные:
Система уравнений (1) и её решения (2) имеют простой геометрический смысл.
Рассмотрим трехмерное пространство
Тогда
формула (2) определяет некоторую линию
в параметрическом виде, причем в роли
параметра выступает переменная x.
Обозначим
Уравнение
линии можно записать в виде:
Линия (2),(2’) назовется интегральной линией системы уравнений (1’)
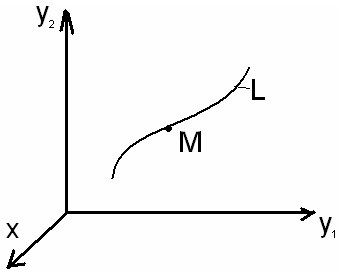
Если для произвольной точки M
подсчитать значение правых частей
системы (1’), то мы будем знать направление
касательных к линиям
и
к
проецированием интегральной линией
Следовательно, система (1’) задает нам
направление в пространстве
Интегральная линия – это линия в каждой своей точке идущая вдоль ‘поля’ т.е. линия в которой точке, которой касательная имеет направление, заданная этим полем.
В системе (1’) переменные
равноправны, переменная x
имеет иное значение. В некоторых
случаях все три переменные равноправны,
так что любую из них можно принять за
зависимую: тогда систему уравнений
предлагается записать в симметричной
форме:
(3)
От системы (3) можно перейти к системе (1’) и наоборот:
Геометрический смысл системы (3) аналогичен описанному ранее.
Вектор
в
любой заданной точке М(x,y,z)
в силу соотношения (3) должен быть
параллелен вектору
Таким образом задача об интегрировании (3) – это задача о построении линии в пространстве имеющей в каждой своей точке заданное направление .
Для однозначного определения интегральной
линии надо задать точку
в пространстве, через которую эта линия
должна пройти. Другими словами. Начальное
условие
однозначно
определяет решение системы (1’)