Радикальный признак Коши, сходимости рядов с положительными членами

Теорема: Если предел от n-го члена ряда вида , то если l<1 то ряд сходиться, l>1- расходиться.

Доказательство:

Пусть l<1 выдержим число q в l<q<1 зафиксируем в качестве положительную величину q-l согласно определению предела для заданной величины найдется номер N что для всех будет выполнить неравенство:

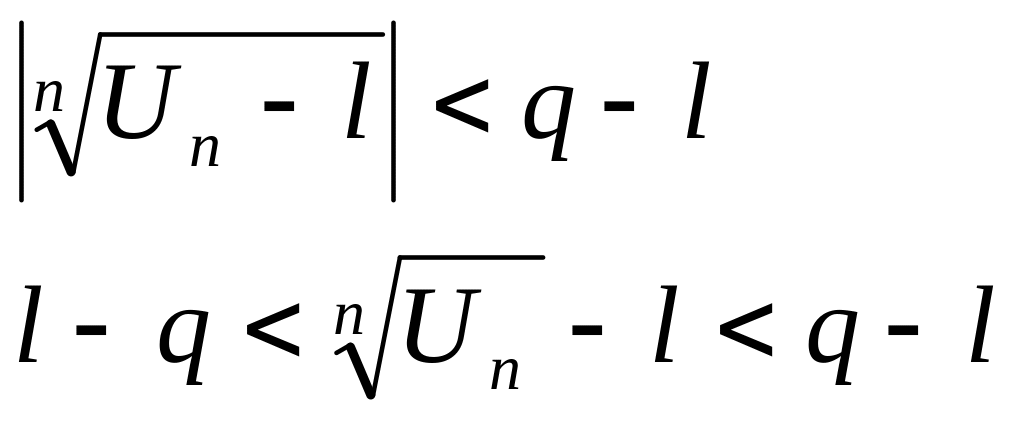
В силу правого неравенства получаем:

Получаем что

Для нумеровки , то есть можем записать последовательность неравенств:

Наряду с исходными рядами выпишем вспомогательный ряд,

Заметим, что вспомогательный ряд – геометрическая прогрессия со значением вспомогательный ряд сходится, а начиная с номера N члены искомого ряда не больше соотносящихся членов вспомогательного ряда, то есть – заключаем, что при l<1 исходный ряд сходится. Докажем вторую часть теоремы. Пусть l>1 - положительная величина. , согласно определению предела для заданной найдется номер N такой что для всех

Запишем в эквивалентной форме Левую часть неравенства можно переписать в виде (5)

Переходя в неравенстве (5) к пределу при . Откуда в силу необходимости признака сходимости сходимости ряда расходимость рассматриваемого ряда.

Пример:

Используя радикальный признак Коши видим, что n-й член равен

Согласно признаку Каши, ряд сходиться.

Интегральный признак Коши сходимости рядов с положительными членами

Т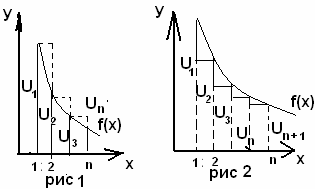 еорема: Если члены ряда (6) удовлетворяет неравенству (7)

И существует непрерывная невозрастающая функция g(x), такая что то из сходимости или расходимости несобственного интеграла:

следует сходимость или расходимость ряда. (6)

Из (1) видим, что высота 1-го прямоугольника равна числу ряда, основание прямоугольника равно 1 высота 2 – го прямоугольника равна 2-му числу ряда, основание равно 1.

Площадь Ступенчатой фигуры изображенной на рисунке (1) равна частичной сумме ряда (6). Площадь кривой трапеции ограниченной функции f(x) определяется

на рис.2 замечаем, что площадь ступенчатой фигуры равна

(9)

Из (9) выражения следует: (9’)

Если несобственный интеграл сходится , то (10)

Из (10) следует последовательности частичной суммы ограничены сверху так как члены ряда (6) положительны, последовательность частичных сумм возрастает.

По теореме предельного курса следует, что возрастающая и ограниченная сверху функция имеет предел.

Рассмотрим случай, когда несобственный интеграл расходиться . В силу неравенства и расходимость несобственного интеграла . За счет увеличения номера n, может быть сделан больше любого положительного числа A. В силу неравенства (8) заключаем, что за счет выбора номера n частичная сумма может быть больше . Сумма может быть сделана из любого положительного числа A, то есть из расходимости несобственного интеграла расходимость ряда.

Пример: Используя интегральный признак исследовать на сходимость обобщенный гармоничный ряд: обобщенный гармоничный ряд вида:

Легко заметить, что признаки Д’Аланбера и радикальный признаки Коши не позволяют исследовать обобщенный гармонический ряд: при выполняются все условия теоремы об интегральном признаке сходимости ряда, поэтому исследуем вопрос о сходимости ряда, поэтому исследуем вопрос о сходимости несобственного интеграла .

При вычислении, этого интеграла различают 2 случая:

1)

Таким образом, видим, что при , обобщенный гармонический ряд расходиться.

2)

Видим, что величина последнего предела определяется значением . При этом возможно два случая: 1) , 2) .

Если , то и в этом случае предел бесконечен, ряд расходиться.

Если , то величина и в этом случае несобственный интеграл сходится при этом сходится и обобщенный гармоничный ряд.