Автономное уравнение второго порядка

Понизим порядок исходных уравнений второго порядка.

5)Порядок уравнения легко понижается, если удаётся преобразовывать уравнения к такому виду, чтобы обе его части являлись полными производными от каких-либо функций.

Линейные дифференциальные уравнения n-го порядка записываются в виде:

-некоторые заданные функции переменной Х; если правая часть уравнения (1) отлична от 0, то дифференциальное уравнение называется неоднородным, если правая часть уравнения (1) равна 0, то дифференциальное уравнение называется однородным. Левую часть уравнения (1) принято обозначать в виде:

означает взятие от функции у соответствующих производных, умножения производных на коэффициенты и последующее их сложение.

Символ называется линейным дифференциальным оператором. Исходя из правила дифференцирования суммы, законов дистрибьютивности, ассоциативности, коммутативности, замечаем, что оператор удовлетворяет следующим двум свойствам:

= +

Линейные однородные уравнения n-го порядка

Если и является решением уравнения (3), то выполняются тождества:

Если есть частное решение уравнения (3), то функция также является решением уравнения (3).

Следствие 1: Если - частное решение уравнения (3), то линейная комбинация этих уравнений также являются решением линейного однородного уравнения (3).

Следствие 2: Если известны частные решения уравнения (3) , то функция (4) также является решением уравнения (3). Это решение содержит n-констант и если все эти константы существенны, то выражение 4 даёт общее решение дифференциального уравнения (3).

Тривиальное решение рассматривать не будем.

Функции называются линейно зависимыми на , если существуют наборы чисел , хотя бы одно из которых отлично от 0, такое, что выполняется равенство во всех точках х, рассматриваемого интервала. Если не существуют наборы чисел , то функции называются линейно независимые.

Определитель Вронского

Пусть имеется n функций имеющих непрерывные производные до n-1 порядка включительно, тогда выражение:

(5) называется определителем Вронского, или вронскиан функции.

Теорема: Если функции линейно зависимые, то определитель Вронского тождественно равен 0, на рассмотренном интервале.

Доказательство: Пусть функции линейно зависимые, тогда существует набор чисел , хотя бы одно из которых отлично от 0, такое, что будет выполняется соотношение:

, тогда можно переписать в виде:

Продифференцируем выражение до n-1 порядка включительно:

рассмотрим определитель Вронского от этих функций. Умножим первый столбец этого определителя на и отнимем его из последнего столбца:

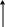
Поступая аналогично с n-1 столбцом, получим определитель, численно равный исходному. В силу (7), (7’), последний столбец преобразованного определителя будет состоять из нулей, следовательно определитель Вронского в этом случае равен 0.

Теорема: Если функции являются решениями уравнения (3) и линейно независимы, то определитель Вронского не обращается в ноль ни в одной точке рассматриваемого интервала.

Доказательство: предположим противное, что набор частных решений линейно зависим в некоторой точке интервала , т.е. определитель Вронского в точке .

Составим линейную комбинацию . Производная от линейной комбинации:

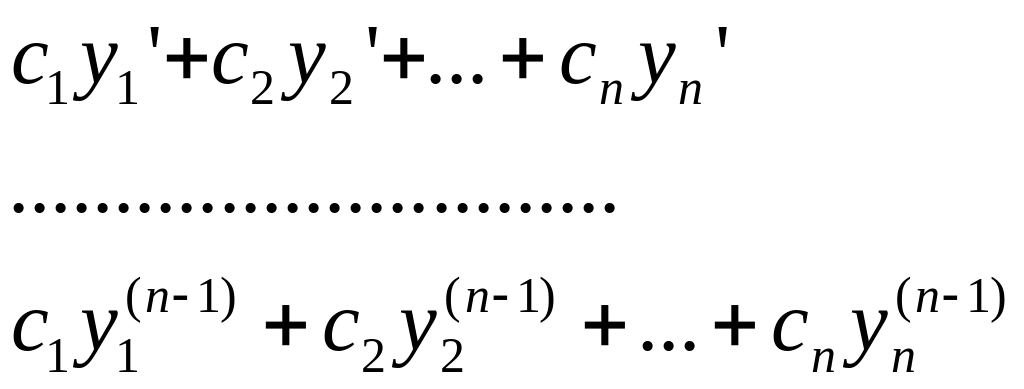
Возьмем и прировняем эти выражения к нулю:

Таким образом, получили систему линейных однородных уравнений относительно переменных . Корневой определитель этой системы является определителем Вронского в точке и он равен нулю, следовательно, выписанная система линейных уравнений является неопределенной, обладает бесконечным множеством решений. Выберем частные решения этой системы , так, чтобы не все элементы обращались в 0. При этом, согласно следствиям из теоремы о линейных однородных уравнениях , получим, что функция будет являться решением линейного однородного уравнения (3). Это решение удовлетворяет начальным условиям , .

Таким образом функция удовлетворяет начальным условиям (8).

В силу теоремы о существовании и единственности решения дифференциального уравнения n-го порядка заключаем, что решение единственно, при этом этим же условиям удовлетворяет тривиальное решение , откуда вытекает, что .

, т.е. получим, что функция линейно зависимые, полученное противоречие доказывает теорему.

Определение: Любая система из n-линейнонезависимых частных решений однородного линейного уравнения n-го порядка называется фундаментальной системой решения.

Если фундаментальная система решений уравнения, то общее решение можно записать в виде: .

Теорема: Для всякого линейного однородного диференциального уравнения существует фундаментальная система решений.

Пример:

найти общее решение дифференциального уравнения.

, - это функция является решением выписанного уравнения. Замечаем, что , проверим, являются ли эти функции линейно зависимыми , .

, следовательно, эти функции линейно независимы. Определитель Вронского позволяет, зная фундаментальную систему решений, легко построить соответствующие дифференциальные уравнения, для этой цели приравнивают к 0 определитель Вронского.

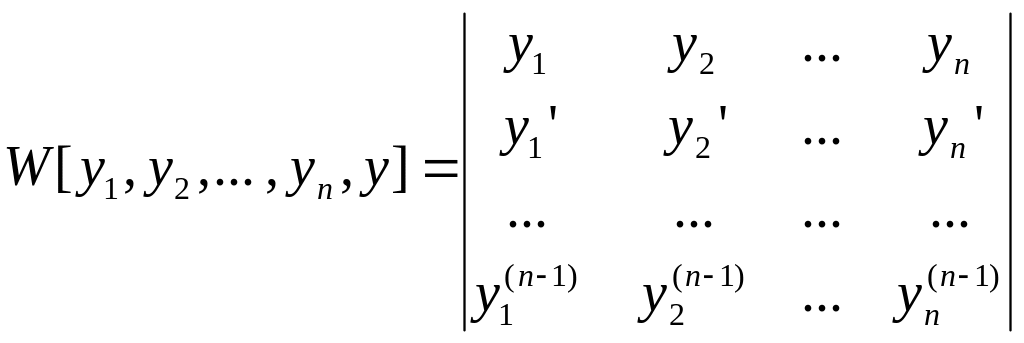
Очевидно что, подставляя вместо последнего столбца частное решение , будем обращать выделенный определитель в тождественный ноль. Чтобы выписать явный вид дифференциального уравнения, раскроем определитель по элементам последнего столбца.

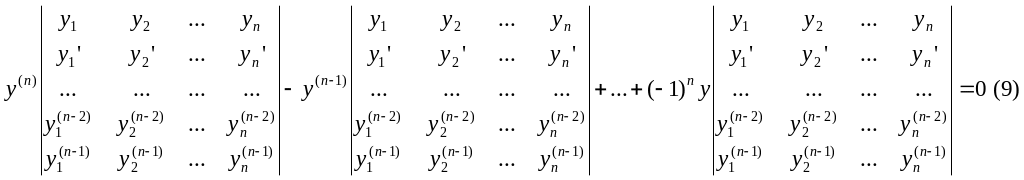Замечаем, что коэффициент, стоящий при старшей производной является определителем Вронского от . Так как система функций является фундаментальной, то этот определитель отличен от 0. Разделив (9) на определитель Вронского можно переписать линейное уравнение в виде:

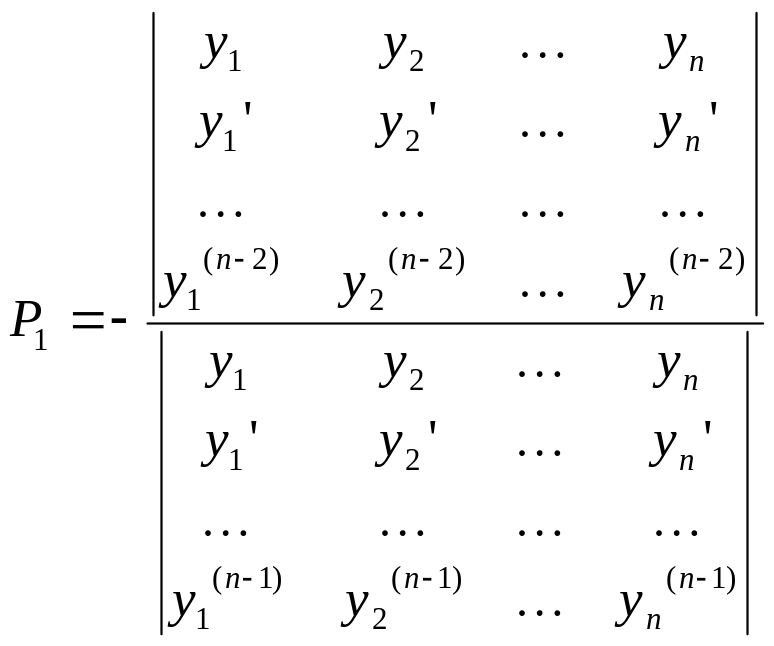(10)

Определитель Вронского принято обозначать W(x). Можно заметить, что определитель, стоящий в числителе выражения является производной определителя Вронского. Следовательно, соотношение (10) можно переписать в виде: (10’). Разделяя переменные по соотношению (10’) получим .Интегрируя последнее соотношение находим: . Записав первообразную в виде интеграла с переменным верхним пределом, можем преобразовать последнее выражение в виде: (11)

Соотношение (11) называют формулой Остроградского – Лиувилля

Формула (11) может быть применена для нахождения общего решения линейного однородного уравнения второго порядка у которого известно одно частное решение.

Пример:

Пусть дано дифференциальное уравнение второго порядка

- частное решение этого уравнения. Составим из функции и определитель Вронского:

Раскроем определитель стоящий слева:

Разделив обе части последнего соотношения получим :

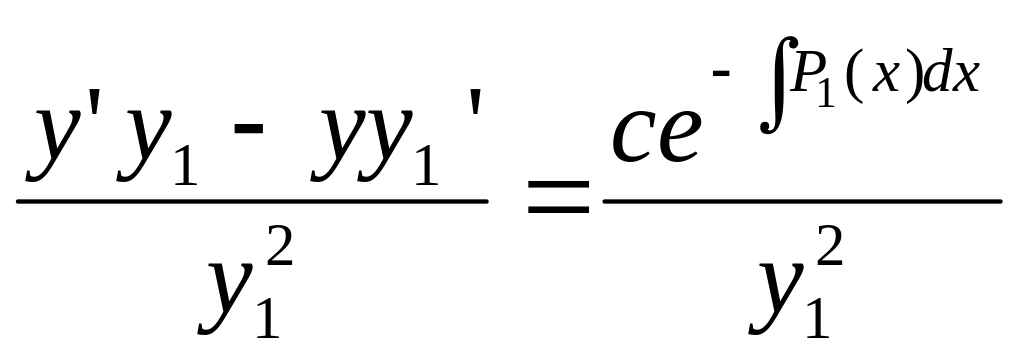
Замечаем, выражение слева является полной производной от

. Таким образом проинтегрировав выписанное дифференциальное соотношение найдем: 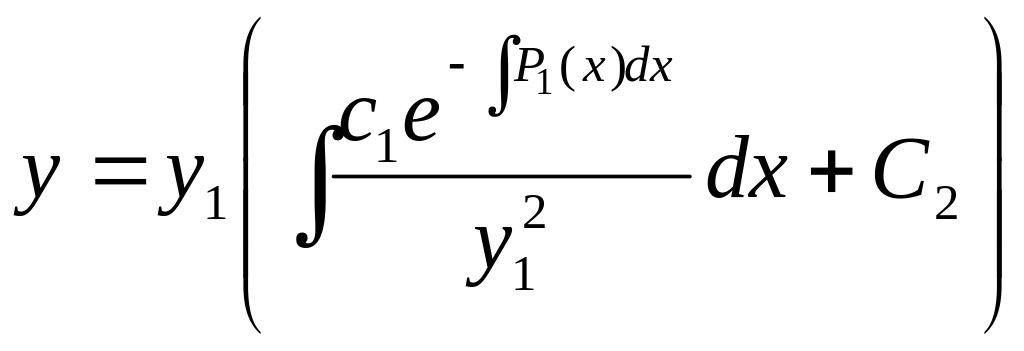(12)

Формула (12) дает общее решение линейного однородного дифференциального уравнения второго порядка при известном частном решении.

Пример:

Рассмотрим дифференциальное уравнение: ,

Заметим, что частным решением является:

Выпишем величину для данного уравнения и заметим, что она равна используя формулу 12 запишем общее решение этого дифференциального уравнения.

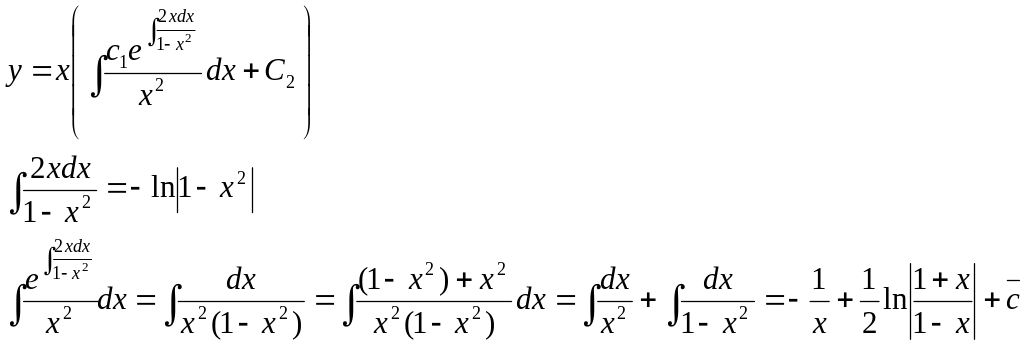
Таким образом, общее решение: