Особые точки

Рассмотрим случай, когда нарушается условие а) теоремы о существовании решения. Пусть функция неограниченна в точке , при этом необходимо рассмотреть 2 случая:

1)

В этом случае функция , при . Доопределим эту функцию в т. нулевым значением, тогда дифференциальное уравнение первого порядка можно рассматривать как дифференциальное уравнение функции х, зависящей от у: в этом случае функция, стоящая справа, удовлетворяет условиям теоремы существования. При этом касательная к интегральной кривой будет располагаться перпендикулярно оси х. Других особенностей в точке в этом случае не будет..

Пример:

Рассмотрим дифференциальное уравнение вида : . Видим, что в указанной точке нарушается непрерывность. Функция, стоящая справа, стремится к бесконечности. Рассматривая обратную функцию, получим: , откуда , подставляя начальные условия, найдем решение в виде: -парабола.

Функция не ограничена и не имеет предела при стремлении к точкам . В качестве примера такой функции, рассмотрим функцию , . При изучении непрерывности функции многих переменных показывали, что эта функция не имеет предела в точке (0, 0). Видим, что переходя к обратной функции не сможем ликвидировать особую точку, так как получим выражение такого же вида. В этом случае точка является особой точкой дифференциального уравнения. Поведение интегральных кривых около особой точки (0,0) зависит от величины параметров: а, b, c, k.

Особые решения

Особыми решениями называются такие решения дифференциального уравнения, которые во всех своих точках не удовлетворяют условию единственности. Особое решение получается в том случае, когда нарушается условие б) теоремы существования, при этом липшитцевость функции обычно заменяется неограниченностью производной . Если точки, в которых неограниченна, образуют линию, то необходимо проверить является ли эта линия решением дифференциального уравнения и нарушается ли в ее точках единственность решений. Если линия является решением и нарушается единственность, то найденная линия дает особое решение дифференциального уравнения.

Пример:

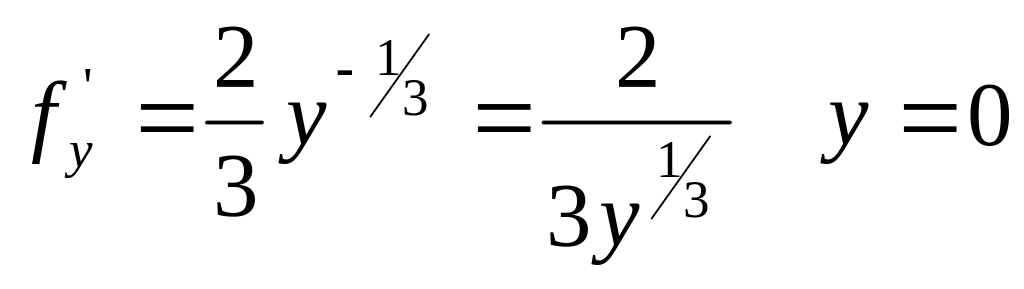в дифференциальном уравнении.

Убеждаясь, что функция является ее решением для того, чтобы показать, что найденные решения являются особыми, найдем общее решение данного дифференциального уравнения.

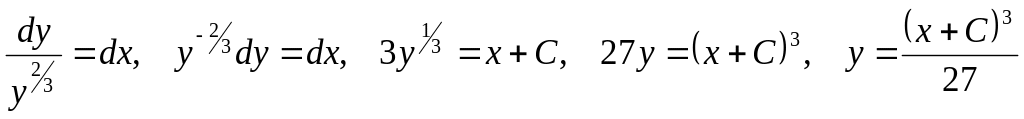
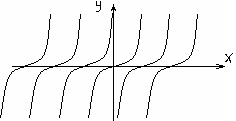
Через каждую точку оси х проходят кривые, являющиеся решением дифференциального уравнения. Выражение у=0 дает особое решение рассматриваемого дифференциального уравнения. Если известно общее решение дифференциального уравнения, то особое решение во многих случаях может быть найдено в качестве огибающей семейства общих решений. Если (х,у,с)=0, дает общее решение дифференциального уравнения, то для построения огибающей находят частную производную , , из полученной системы исключают параметр с. Построим особое решение , используя общее решение рассмотренного ранее. Найдем частную производную по с о общего решения: .