Теорема Абеля

Если - радиус сходимости степенного ряда (1), то степенной ряд сходится не только абсолютно и равномерно на любом отрезке . Если, кроме того, степенной ряд сходится при или при , то он будет равномерно сходиться на отрезке или .

Свойство сторонних рядов

Степенной ряд (1) радиус сходимости которого равен R, есть непрерывная функция от x на интервале (-R,R). Степенной ряд можно почленно дифференцировать и интегрировать сколько угодное число раз, пока x принадлежит интервалу (-R,R). Получаемые при этом степенные ряды также имеют радиус сходимости R.

Доказательство: рассмотрим степенной ряд:

Пусть R-его радиус сходимости согласно второй теореме Абеля степенной ряд (1) сходится равномерно на (-R,R), следовательно согласно первому свойству равномерно сходящихся функциональных рядов, сумма ряда (1) – непрерывная функция на интервале (-R,R). Проинтегрируем члены ряда (1), получим степенной ряд:

(5)

(6)

Сходимость ряда (5) вытекает из второй теоремы Абеля и второе свойство равномерно сходящихся двух функциональных рядов.

Покажем, что ряд (6) также будет сходиться на интервале (-R,R), возьмем некоторое значение х из (-R,R). Подберем число S удовлетворяющее неравенству

Обозначим отношение.

. Выполним оценку абсолютных величин членов ряда (6).

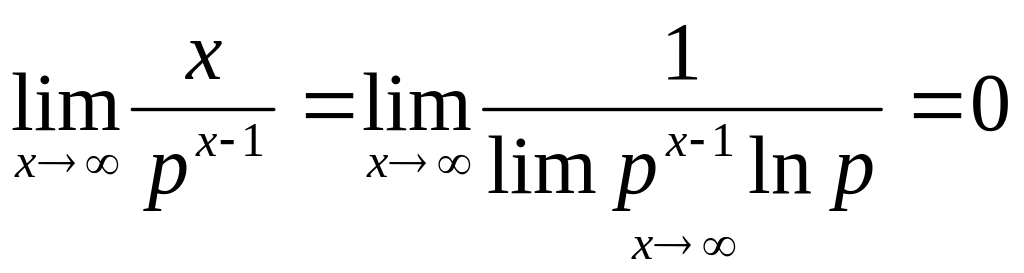
Так как lim последовательности = 0, то для выбранной величины S можно подобрать номер N, такой чтобы для всех , будет выполняться , следовательно, .

Отбрасывания конечного числа слагаемых не влияет на сходимость ряда. (8)

Рассматривая ряд (6) начиная с номера N заключаем, что его члены будут меньше членов ряда.

(9) сходимость следует из соотношения (7), следовательно ряд (6 сходится на интервале (-R,R). Таким образом, покажем, что R не может уменьшаться. Покажем, что при дифференцирование R ряда не уменьшается. Если бы при дифференцировании степенного ряда получили радиус сходимости больше R, то проинтегрировав полученный степенной ряд, получили бы ряд, радиус сходимости которого был бы равным R, так как в результате интегрирования вернулись бы к исходному ряду, то получили бы противоречие R₁>R, следовательно, при дифференцировании R не меняется. Заметим, что степенным рядом является функцией ряда вида:

Видим, что при степенной ряд (10) превращается в степенной ряд (1). Для определения R сходимости степенного ряда (10) проводят замену переменной:

Получили степенной ряд положительный по Х. Если R – радиус сходимость ряда (11), то ряд (11) сходится для всех , то возвращаясь к X получим область сходимости ряда 10.

Ряды Тейлора и Маклорена

Если для функции в окрестности точки е производится до n+1 прежде в локальных, то имеет место формула Тейлора.

, где - остаточный член в форме Лагранджа имеет вид:

Если функция имеет вид производной всех порядков в окрестности точки , то в формуле Тейлора число n можно брать сколько угодно большим, если , то функция может быть представлена . Отметим, что функция представляет рядом Тейлора, только в том случае, когда предел остаточного члена больше нуля, при , если , то ряд Тейлора превращается в ряд Маклорена.

Известно, что для каждой элементарной функции существуют такие величины что в интервале элементарные функции располагаются в ряд Тейлора, другими словами, каждая элементарная функция может быть представлена некоторым степенным рядом, обратное утверждение в общем случае несправедливо – не всякая функция представляется сходящимся степенным рядом, является элементарной.

Функции представляющиеся сходимым степенным рядом называются аналитическими. Примеры использования степенных рядов.

Бипоминальный ряд: Разложен на ряд Маклорена

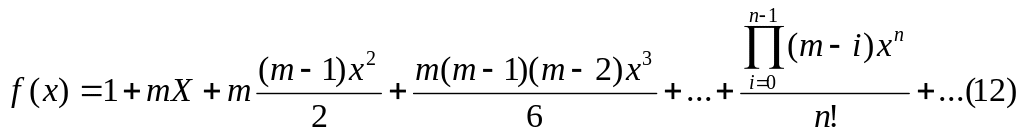, таким образом - биноминальный ряд

Определим радиус сходимости биноминального ряда.

Таким образом, видим, что биноминальный ряд (12).

Вычислим предел отношения:

Таким образом, видим, что биноминальный ряд (12) сходится при условии, что .

Если m-целое положительное число, то начиная с номера все коэффициенты равны нулю. Ряд превращается в ряд Ньютона.

Рассмотрим биноминальный ряд при m=-1.

Это геометрическая прогрессия

Биноминальный ряд примет вид:

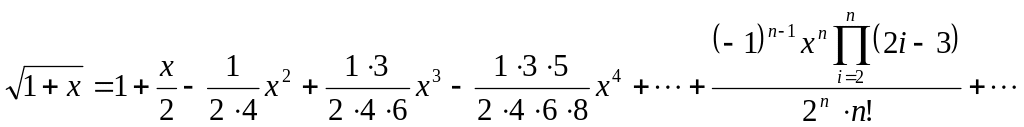
Заметим, что знаменатель можно представить в виде:

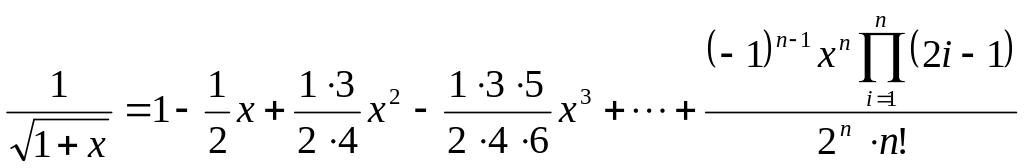
Применим биноминальный ряд к разложению других элементарных функций. Разложим логарифмическую функцию степенного ряда.. Заметим, что можно представить в виде:

Подынтегральную функцию заменим соответствующим интегральным рядом:

Используя свойства степенных рядов, поменяем знак суммы и знак интеграла:

Пример:

Разложим степенной ряд . Для этого заметим, что можно представить в виде: = воспользуемся биноминальным рядом для случая

Используя выписанное разложение получим: =
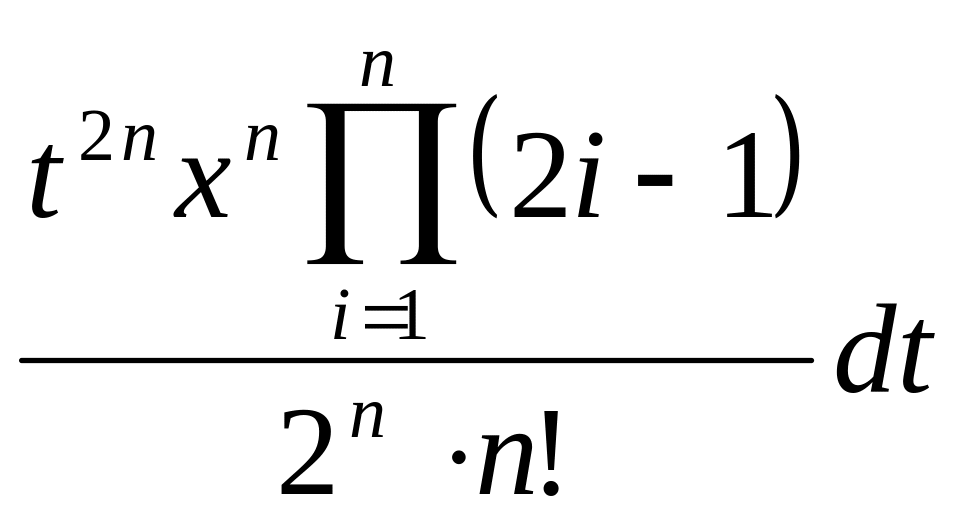