Свойство равномерно сходящихся рядов

Если в предыдущих предположениях рассматривали как частичную сумму ряда (1) тогда когда будет суммой всего ряда и можно записать аналогичные свойства для равномерно сходящихся функциональных рядов.

Свойство 1: Если члены ряда(1) непрерывной на функции и ряд сходятся равномерно, то его сумма есть непрерывная функция на .

Свойство 2: Если члены ряда (1) непрерывной на интервале функции и ряд сходится равномерно, то его можно почленно интегрировать между любыми пределами , лежащими в , т.е.

(2).

Если пределы интегрирования переменные, например, , то ряд полученный почленным интегрированием ряда(1)

(3) также равномерно сходится на .

Свойство 3: Если ряд (1) сходится на и его члены имеют непрерывные на производные. Причем ряд, составленных производных сходится равномерно на , то и заданный ряд (1) сходится равномерно и его можно почленно дифференцировать.

.

Достаточный признак равномерной сходимости функционального ряда.

Признак Вейерштрасса

Ряд функций, определенных на , сходится равномерно на этом интервале, если можно указать последовательность положительных чисел такую, что для всех Х из будет выполняется неравенство и ряд из положительных членов сходится, . В этом случае говорят, что функциональный ряд мажорирует.

Доказательство: Для доказательства признака Вейерштрасса достаточно показать, что в этом случае выполняется признак Коши, равномерной сходимости ряда, т.е. для любого положительного числа можно указать номер , такой что для всех , всех натуральных р и всех точек , выполняется неравенство.

(***)

Поскольку ряд из положительных членов сходится, то для можно указать номер N, что для всех будет выполняться неравенство: . В силу неравенства (*) из (**) вытекает (***).

Пример:

Исследовать на равномерную сходимость функциональный ряд вида:

n-ный член ; .

- сходится, а это означает, что сходится равномерно и выписанный функциональный ряд.

, является неопределенной функцией.

Степенные ряды. Радиус сходимости

Степенным рядом называется функциональный ряд вида: (1), - некоторые заданные числа.

Первая теорема Абеля: Если степенной ряд(1) сходится при некотором значении , то он сходится абсолютно для всех значений , удовлетворяющих неравенству . Если ряд (1) расходится при некоторых значениях , то он расходится для всех при .

Согласно условию теоремы при x=S сходится числовой ряд.

S-некоторое число

n-нный член числового ряда имеет вид:

, т.к. ряд (1) сходится, согласно необходимому признаку сходимости ряда:

=> для положительного числа M найдется номер N такой, что для всех будет выполняться неравенство

Выбираем в качестве (2)

Согласно выбору числа M все члены числового ряда удовлетворяют неравенству .

Рассмотрим ряд из абсолютных величин членов ряда (1).

(3)

Представим члены ряда (3) в виде:

(3’)

Члены ряда (3’) меньше соответствующих членов ряда:

то ряд (4) представляет собой сходящуюся геометрическую последовательность. Следовательно, ряд (4) сходится при условии, что при этом сходится ряд (3) и следовательно ряд (1) расходится при необходимо показать, что ряд (1) будет расходиться при всех х, удовлетворяющих

Допустим противное, пусть ряд (1) сходится при некотором значении x удовлетворяющем неравенству тогда согласно доказанной первой части теоремы степенной ряд (1) должен сходится и при значении S. Так как при ряд расходится, полученное противоречие доказывающее вторую часть теоремы Абеля.

Следствие: Если существует положительное число N называемой радиусом сходимости R. Число R обладает свойством степенного ряда (1) сходится при всех и расходится при всех в граничных точках интервала степенной ряд может как сходиться, так и расходиться.

Радиус сходимости R может выражаться в одну точку, при этом степенной ряд сходится только при Существуют также степенные ряды радиус которых бесконечен, такие ряды сходятся при любых значениях x.

Для определения радиуса сходимость степенного ряда обычно используют признак Да Лан Бера или признак Каши. Для того, чтобы использовать признак Да Лан Бера и Коши рассматривают:

(1)

Ряд сходится для всех x, удовлетворяющих 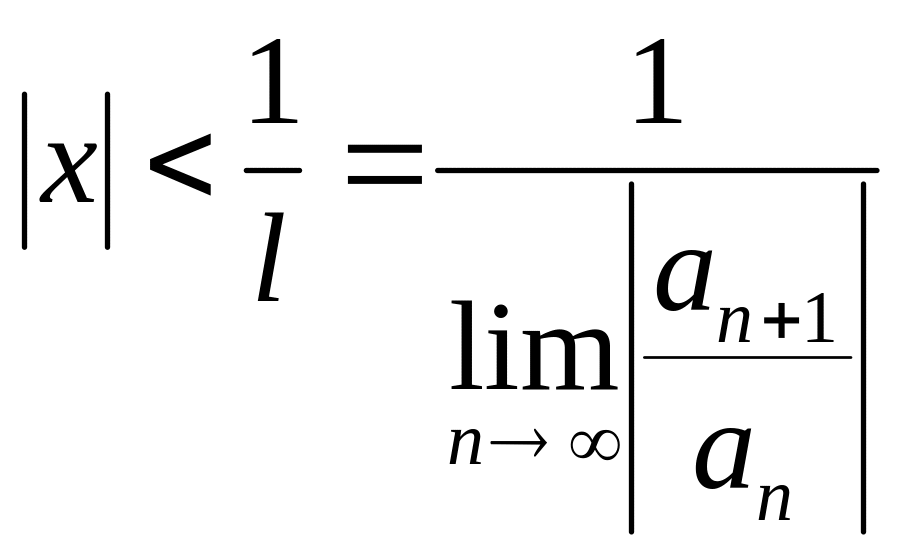=> Радиус сходимости степенного ряда может быть вычислен соотношением: . В случае использования радикального признака Коши получим: .
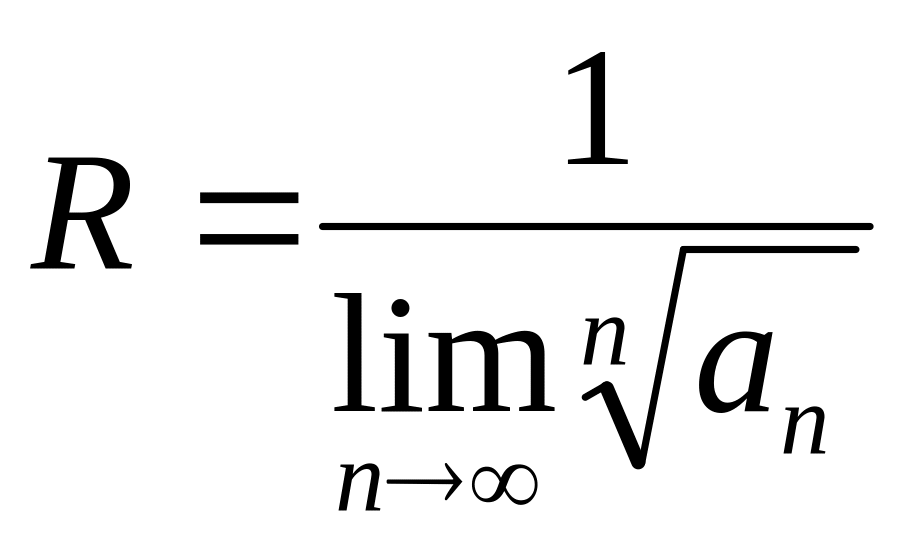