Ряды Фурье

Рассмотрим ряд Макларена:

…+ …

Ряд Макларена можно рассматривать, как разложении функции по бесконечномерному базису: при этом коэффициенты ряда Макларена обеспечивают наилучшее приближение функции, соответствующие частичной суммы. Как было показано в алгебре, особую роль играют ортогональные базисы.

Определение: Функции называются ортогональными на отрезке , если выполняются условия:

.

Исторически первой и наиболее важной системой ортогональной функции на отрезке , явилась функция:

Покажем, что система уравнений (1) образована из попарно ортогональных функций.

1.

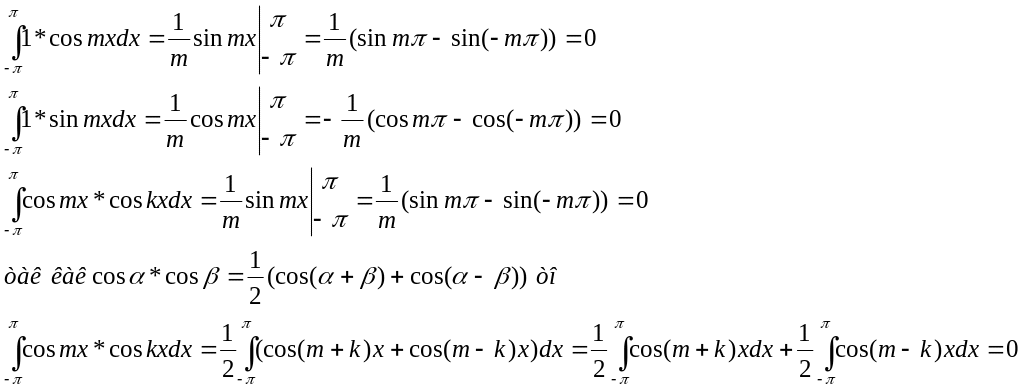
Таким образом показали, что система функций (1) попарно ортогональна. Из курса линейной алгебры известно, если вектор x разложить по ортогональному базису:

- ортогональный базис. По координатам вектора x можно вычислить по следующему соотношению.

Умножим скалярно разложения (2) на вектор . В силу соотношения (*) получим

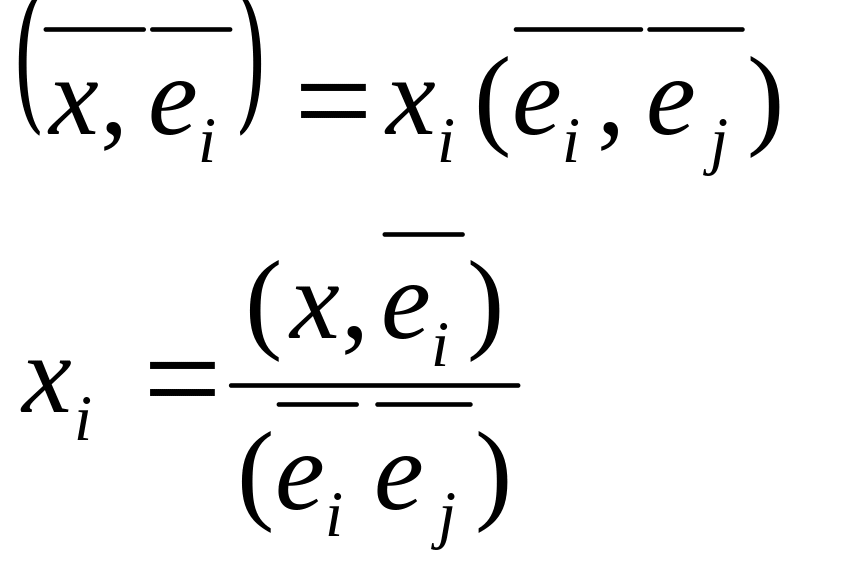
Теорема: Если функция f(x) периодическая с периодом частично монотонная и ограниченная, то она разлагается в ряд по функциям системы (1)

Этот ряд называется тригонометрическим (рядом Фурье) в точках непрерывности функции f(x) значение ряда совпадает с соответствующим значением функции f(x).

Если С – точка разрыва функции, f(x), S(x),- сумма тригонометрического ряда.

То

Получим выражение для коэффициентов ряда Фурье, для периодической функции f(x)

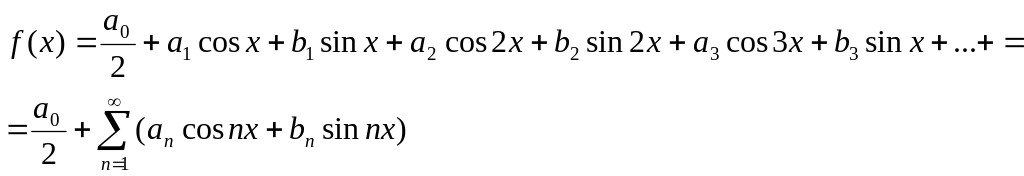(4)

Выражение (4) называется тригонометрическим рядом, или рядом Фурье.

В соответствии с соотношением (3) для определения коэффициента , умножим обе части выражения (4) на (1), затем вычислим интегралы на отрезке от , то в силу ортогональности функции (1) получим

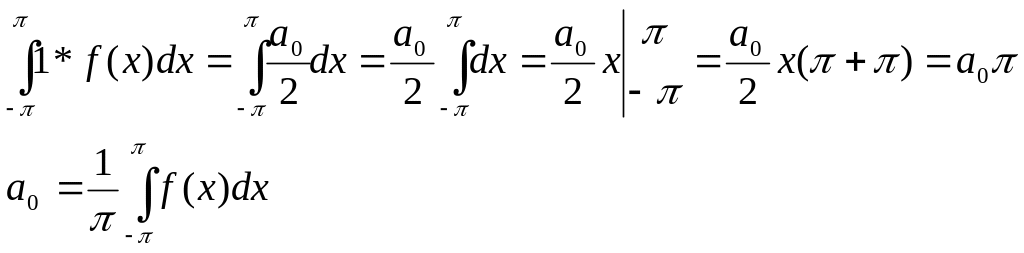
Для определения коэффициента умножим обе части соотношения (4) на (как было показана ранее 2-ой интеграл)

Для определения величин умножим обе части соотношения (4) на . После интегрирования на отрезке получаем: .

Если - периодическая функция, с периодом , то для её разложения в ряд Фурье, выполним замену так, чтоб вспомогательная функция имела период .

, видим, что

Выполним замену переменной

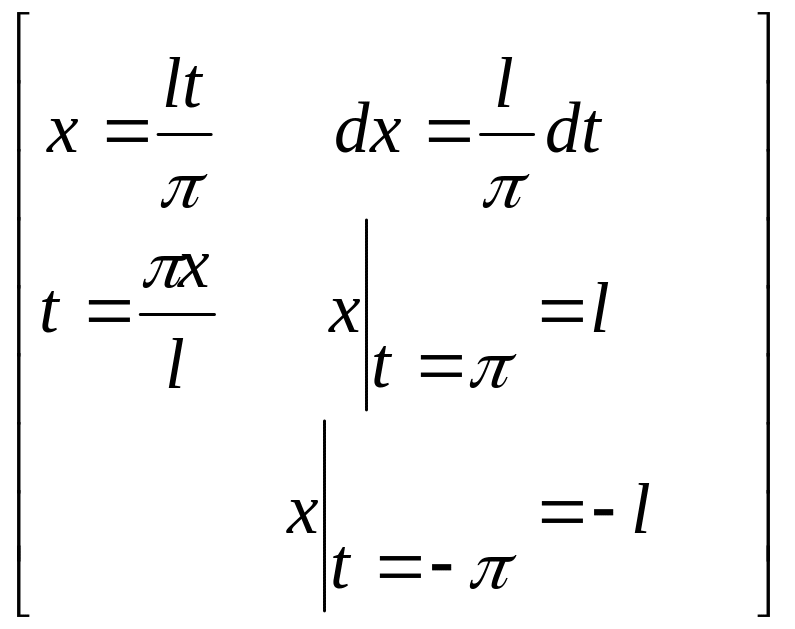
Получим выражение для коэффициентов

Вычисляем по формуле (5)

Ряды Фурье для чётных и нечётных функций

Из определения четной и нечетной функции следует, что если ψ(x) – четная функция, то

.

_{Действительно,}

_{так как по определению четной функции ψ(- x) = ψ(x).}

_{Аналогично можно доказать, что если ψ(x) – нечетная функция, то}

_{Если в ряд Фурье разлагается нечетная функция ѓ(x), то произведение ѓ(x) ·coskx есть функция также нечетная, а ѓ(x) · sinkx – четная; следовательно,}

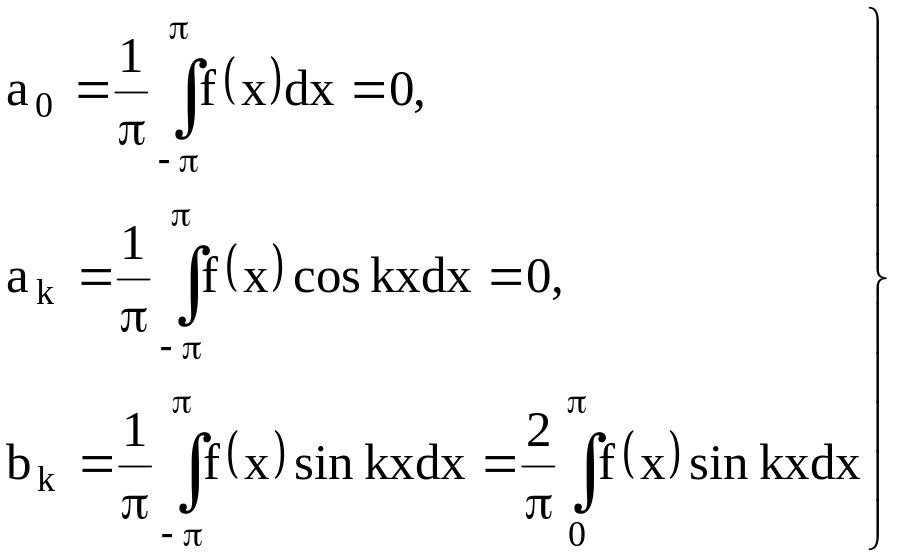₍₂₁₎

_{т. е. ряд Фурье нечетной функции содержит «только синусы».}

_{Если в ряд Фурье разлагается четная функция, то произведение ѓ(x) · sinkx есть функция нечетная, а ѓ(x) · coskx – четная, то:}

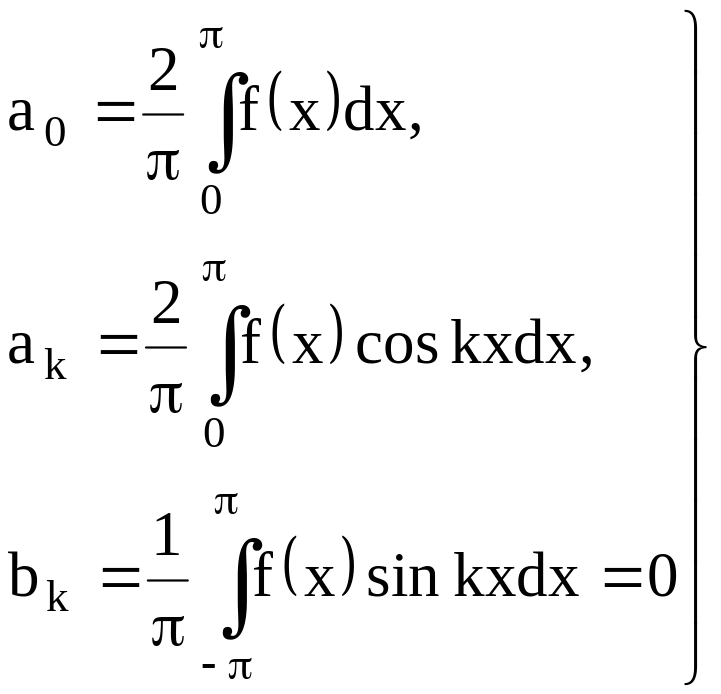₍₂₂₎

_{т. е. ряд Фурье четной функции содержит «только косинусы».}

_{Полученные формулы позволяют упрощать вычисления при разыскании коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Очевидно, что не всякая периодическая функция является четной или нечетной.}

Пример:

Разложить в ряд Фурье периодическую функцию  с периодом T = 2 на отрезке [- ; ].

 Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

 

 

 

 

 

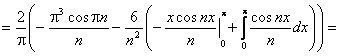
 Получаем:

.

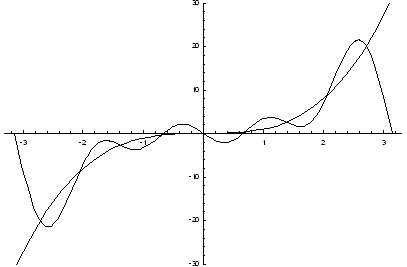
   Построим графики заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.