
- •Дифференциальные уравнения.
- •Обыкновенные дифференциальные уравнения первого порядка.
- •Элементарные методы интегрирования (оду первого порядка)
- •I. Дифференциальное уравнение первого порядка не содержащее явно искомую функцию.
- •II. Однородные дифференциальные уравнения первого порядка.
- •III. Линейные дифференциальные уравнения 1-го порядка.
- •IV. Уравнение Бернулли:
- •V. Уравнения полных дифференциалов:
- •Особые точки
- •Особые решения
- •Обыкновенные дифференциальные уравнения высших порядков
- •Автономное уравнение второго порядка
- •Линейные однородные уравнения n-го порядка
- •Определитель Вронского
- •Неоднородные линейные дифференциальные уравнения n-го порядка
- •Метод вариации постоянных
- •Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами
- •Системы обыкновенных дифференциальных уравнений
- •Дифференциальные уравнения 1-го порядка
- •Геометрический смысл системы уравнений первого порядка
- •Первые интегралы
- •Линейные системы с постоянными коэффициентами
- •Устойчивость положения равновесия (устойчивость по первому приближению)
- •Сравнение рядов с положительными членами
- •Расходимость гармонического ряда
- •Радикальный признак Коши, сходимости рядов с положительными членами
- •Интегральный признак Коши сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Теорема Лейбница.
- •Знакопеременные ряды. Абсолютная и условная сходимости знакопеременных рядов.
- •Достаточный признак сходимости знакопеременного ряда
- •Действия над сходящимися рядами
- •Умножение абсолютно сходящихся рядов
- •Функциональные ряды
- •Критерии Коши равномерной сходимости функционального ряда
- •Функциональная последовательность
- •Свойства равномерно сходящихся функций последовательностей
- •Свойство равномерно сходящихся рядов
- •Признак Вейерштрасса
- •Степенные ряды. Радиус сходимости
- •Теорема Абеля
- •Свойство сторонних рядов
- •Ряды Тейлора и Маклорена
- •Вычисление определенных интегралов
- •Интегрирование линейных дифференциальных уравнений с помощью степенных рядов
- •Ряды Фурье
- •Ряды Фурье для чётных и нечётных функций
- •Разложение в ряд Фурье непериодической функции
- •Интеграл Фурье
Вычисление определенных интегралов
Существуют определенные интегралы, которые как функции переменного верхнего предела не выражаются через элементарные функции, такие интегралы часто могут быть вычислены с помощью степенных рядов.
Пример:
![]() .
.
Разложим подынтегральную функцию в степенной ряд. Для этого воспользуемся разложением sin в ряд Макларена.
![]()
Известно, что сходящиеся ряды можно
складывать, вычитать, умножать на число,
и если ряды сходятся абсолютно их можно
перемножить. Умножим степенной ряд для
sin на
![]() ,
в результате получим ряд:
,
в результате получим ряд:
![]()
![]() .
.
Подставим полученный степенной ряд под
знак интеграла:
![]()
![]() =
=![]() =
=![]()
![]()
Интегрирование линейных дифференциальных уравнений с помощью степенных рядов
Известно, что решение линейных дифференциальных уравнений с переменными коэффициентами выше первого порядка в общем случае не выражаются через элементарные функции. Наиболее употребительный прием получения решения является поиск решения в виде степенного ряда. Продемонстрируем процедуру поиска решений, для случая решения линейного дифференциального уравнения второго порядка.
Рассмотрим дифференциальное уравнение в виде:
![]()
Предположим, что функции
![]() разлагаются в степенные ряды, пусть:
разлагаются в степенные ряды, пусть:
![]()
![]()
Где коэффициенты
и
![]() ,
считаются известными числовыми
значениями. Будем искать решение
уравнения (1) также в виде степенного
ряда:
,
считаются известными числовыми
значениями. Будем искать решение
уравнения (1) также в виде степенного
ряда:
![]()
Подставим выписанные степенные ряды в дифференциальное уравнение (1):
![]()
![]()
Подставляя в (1), найдем:
![]()
![]()
![]() +
+![]()
![]()
Поскольку степенные ряды в области сходимости сходятся абсолютно, то их можно перемножить. Заметим, что соотношение должно выполняться тождественно для всех значений х. Подставим в величину х=0, получим:
![]()
Продифференцируем тождество по переменной х:
![]()
![]()
![]() +
+![]()
![]()
Подставим в полученное выражение величину х=0, получим:
![]()
Поступая аналогично, получим также уравнение:
![]()
Видим, что система (2) есть система
линейных однородных уравнений относительно
переменных
![]() .
Видим, что система (2) имеет форму трапеции
следовательно это система является
неопределенной. Фундаментальная система
решений состоит из двух равномерных
векторов. Выберем величины
.
Видим, что система (2) имеет форму трапеции
следовательно это система является
неопределенной. Фундаментальная система
решений состоит из двух равномерных
векторов. Выберем величины
![]() ,
,
![]() -свободными
переменными, тогда из первого уравнения
находим величину
-свободными
переменными, тогда из первого уравнения
находим величину
![]() ,
из второго
,
из второго
![]() ,
и т.д.
,
и т.д.
Обычно полагают
![]() ,
=0,
для первого решения, и
,
=0,
для первого решения, и
![]() ,
=1
для второго решения. С учетом степенного
ряда для функции у,
,
=1
для второго решения. С учетом степенного
ряда для функции у,
![]()
![]()
![]()
![]()
Если начальные условия имеют вид:
![]()
![]() ,
то решение будет определяться в виде:
,
то решение будет определяться в виде:
![]()
Пример:
Рассмотрим уравнение:
![]()
Будем искать решение в виде:
![]()
![]()
![]()
![]()
![]()
Здесь неизвестными величинами являются коэффициенты ряда . Приравнивая коэффициенты при равных степенях, получим:
![]()
![]()
![]()
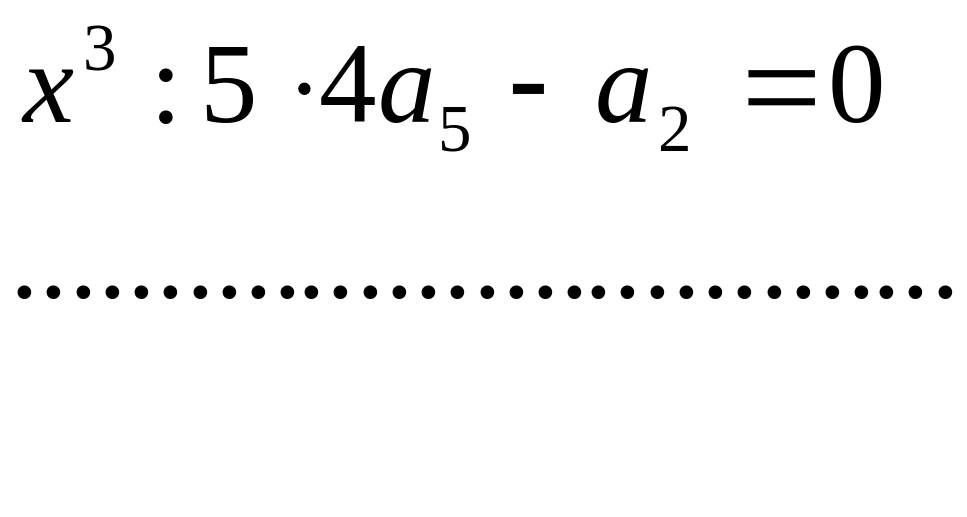
![]()
Полагая,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Замечаем, что отличными от 0 будут те коэффициенты, у которых номер к делится на 3. в это случае получаем:
![]() .
.
Решение
![]() будет в этом случае иметь вид:
будет в этом случае иметь вид:
![]()
Полагая,
![]() ,
,
![]() ,
придем к решению
,
придем к решению
![]() :
:
![]() .
.
Общее решение исследуемого уравнения
можно записать в виде:
![]()
![]()
![]()
