
- •Понятие матрицы. Виды матриц.
- •Линейные операции над матрицами.
- •Умножение матриц. Натуральная степень матрицы. Многочлены от матриц.
- •Элементарные преобразования матрицы, сведение матрицы к треугольному или трапециевидному виду.
- •Определители 2-го и 3-го порядка.
- •Понятие обратной матрицы. Построение обратной матрицы.
- •Понятие системы линейных алгебраических уравнений (слау).
- •Понятие вектора в пространстве. Линейные операции над векторами.
- •Проекция вектора.
- •Линейная зависимость и независимость векторов. Базис.
- •Декартова система координат.
- •3. Базис системы векторов.
- •15.Векторное произведение.
- •16. Смешанное произведение векторов.
- •17. Понятие поверхности второго порядка. Метод параллельных сечений.
- •Цилиндрические и конические поверхности.
- •19.Эллипсоид. Гиперболоиды. Параболоиды.
- •20.Уравнения плоскости в пространстве.
- •22 Уравнения прямой в пространстве.
- •23 Основные задачи на прямую в пространстве
- •24 Прямые и плоскости в пространстве
- •25. Предел функции в точке и на бесконечности.
- •26. Свойство функции, имеющих придел.
- •27.Замечательные пределы
- •28 .Бесконечно малые функции. Эквивалентность бесконечно малых функций. Бесконечно малые ф-ции
- •Эквивалентность бесконечно малых функций
- •29. Односторонние пределы.
- •30. Понятие непрерывности функции в точке. Свойства непрерывных функций.
- •31) Классификация точек разрыва функции
- •32 Понятие производной и правила ее нахождения. Геометрический смысл.
- •33. Производные высших порядков функций, заданных параметрически или неявно.
- •34. Понятие дифференциала первого порядка.
- •Геометрический смысл дифференциала первого порядка.
- •Дифференциалы высшего порядка.
- •37. Необходимые и достаточные условия монотонности и экстремума функции.
- •38. Выпуклость, вогнутость графика. Точки перегиба функции.
- •39.Наибольшее и наименьшее значения функции на промежутке.
- •40. Исследование функции и построение графика.
- •41.Основные понятия функции многих переменных
- •42. Предел функции двух переменных
- •43. Непрерывность функции двух переменных
- •44. Частные производные двух переменных и их геометрический смысл.
- •45. Дифференцируемость и полный дифференциал функции.
- •46. Производная сложной функции. Полная производная.
- •47.Дифференцирование неявной функции.
- •48.Частные производные высших порядков
- •48 Дифференциалы высших порядков
Геометрический смысл дифференциала первого порядка.
Пусть дана нект плоская непрерывная кривая ℓ: y=f(x).
 (.)
M0
(.)
M0
 ℓ -
фиксированная (стационарная) точка
ℓ -
фиксированная (стационарная) точка
y
y

M




∆y





lk
M0


N
y0





x
∆x
x
x0


M0M – секущая
Секущая будет менять свое положение в зависимости от (.) M.
Предельное
положение секущей M0M(если
оно
 при M
→ M0)
- касательная к кривой ℓ в (.)M0.
при M
→ M0)
- касательная к кривой ℓ в (.)M0.
Пусть в системе Oxy кривая задана уравнением y=f(x).
(.) M0(x0,y0); (.)M(x,y);
приращение
функции
 f(x)-f(x0)=
∆f(x)
f(x)-f(x0)=
∆f(x)
y-y0=∆ y
∆ y=f(x+∆x)-f(x0)
Найдём угловой коэффициент секущей M0M из треугольника M0MN:

Зависит только от ∆x.
(.)M
→ (.)M0
 ∆x→0
=> угловой коэффициент касательной,
проведённой к кривой L
в (.)M0
получается предельным переходом в
равенстве (1) при ∆x=0.
∆x→0
=> угловой коэффициент касательной,
проведённой к кривой L
в (.)M0
получается предельным переходом в
равенстве (1) при ∆x=0.

Если lim и он конечен => уравнение касательной к кривой y=f(x) в (.)x0 y-y0=k(x-x0) ↔ k-угловой коэффициент касательной.
Дифференциалы высшего порядка.
 и т.д.
и т.д.
Понятие
производной более высоких порядков,
чем первый, обобщается на любой порядок
n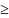 2,
n
N.
2,
n
N.
Порядок
производной, начиная с 4, как правило,
указывается в скобках. Напр.
 .
.

Производная
 порядка n,
n
N
– производная от производной n-1
порядка, т.е.
порядка n,
n
N
– производная от производной n-1
порядка, т.е.
 .
.
Операции дифференцирования n-го порядка обладают свойством линейности, т.е. для производной порядка n справедливы равенства:
Иначе с дифференциалами произведения и частного.
Дифференц. произведение:
Дифференц. 1-го порядка

Дифференц. 2-го порядка

Дифференц. 3-го порядка

Т.о.
производная 2-го порядка для произведения
2-x
функций вычисляется по формуле
аналогичной квадрату суммы, а третьего
порядка аналогично кубу суммы. ММИ
можно легко доказать, что производной
произведения любого порядка n,
 ,
вычисляется по формуле, аналогичной
формуле бинома ньютона, т.е.
,
вычисляется по формуле, аналогичной
формуле бинома ньютона, т.е.
(.)M0
≠ (.)M
 - формула
Лейбница
- формула
Лейбница
При вычислении производного частного деление можно заменить на произведение и применить формулу Лейбница или же дифференцировать дробь последовательно.
37. Необходимые и достаточные условия монотонности и экстремума функции.
Достаточные признаки монотонности функции.
Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум.
Необходимое условие экстремума. Если x0 - точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ ( x0 ) = 0.
Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x 3 равна 0 при x = 0, но эта функция не имеет экстремум в этой точке.
Достаточные условия экстремума.
Если производная при переходе через точку x0 меняет свой знак с плюса на минус, то x0 - точка максимума.
Если производная при переходе через точку x0 меняет свой знак с минуса на плюс, то x0 - точка минимума.


