42. Предел функции двух переменных

Пусть ф-ция z= f (x, y) определена в некоторой окрестности точки (x0 ,y0,), за исключением, может быть, самой этой точки. Число А называется пределом функции z =f (x, y) при x->x0 и y->y0 (или в точке (x0 ,y0,)) если для любого, сколь угодно малого положительного числа E> 0 ,

найдется положительное число б> 0 (зависящее от E), такое, что для

всех точек из б -окрестности точки (x0 ,y0,) , выполняется неравенство | f(x,y)-A |<E

Обозначают:  

43. Непрерывность функции двух переменных

Для функции нескольких переменных можно определить понятие непрерывности.

Функция называется непрерывной в точке 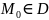, если

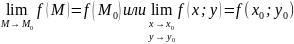
Функция f называется непрерывной в области D, если она непрерывна в каждой точке этой области.

Аналогичным образом определяются понятия предела и непрерывности в точке для функции n переменных, n > 2.

44. Частные производные двух переменных и их геометрический смысл.

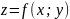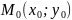Частной производной по переменной х функции в точке называется предел

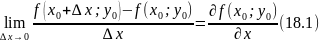
если он существует.

Производную (18.1) обозначают также .

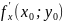Частной производной по переменной y функции в точке называется предел

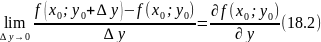
если он существует.

Производную (18.1) обозначают также .

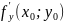Если частные производные определены на множестве 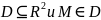, то они являются функциями двух переменных

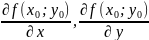
Геометрический смысл.

Пусть поверхность задана уравнением z= f (x;y), (x;y)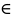 D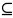 R². Тогда уравнение касательной плоскости в точке M₀ (x₀;y₀) имеет вид:

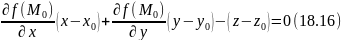
где z₀ = f (x₀;y₀) .

Нормалью к поверхности в точке N₀ (x₀;y₀;z₀) , z₀ = f (x₀;y₀) , называется прямая, проходящая через точку N₀ перпендикулярно к касательной плоскости в этой точке.

Уравнение нормали к поверхности (18.16) в точке M₀ (x₀;y₀) имеет вид:

Если поверхность задана уравнением

F(x; y;z) =0 (18.18)

и в точке N₀ (x₀;y₀;z₀) этой поверхности существуют частные производные 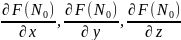не равные нулю одновременно, то уравнение касательной плоскости к поверхности(18.18) в точке N₀ (x₀;y₀;z₀) имеет вид:

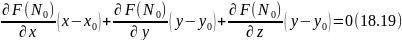
Уравнение нормали к поверхности (18.18) в точке

N₀ (x₀;y₀;z₀) имеет вид:

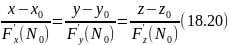
45. Дифференцируемость и полный дифференциал функции.

Дифференци́руемая фу́нкция — это функция, имеющая дифференциал. Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке).

Полный дифференциал функции нескольких переменных. Понятие дифференцируемости функции нескольких переменных.

Функция Z=f(x,y) называется дифференцируемой в точке P(x,y), если ее полное приращение ΔZ можно представить в виде Δz = A∙Δx+B∙Δy+ω(Δx,Δy), где Δx и Δy – любые приращения соответствующих аргументов x и y в некоторой окрестности точки Р, А и В – постоянные (не зависят от Δx,Δy),

ω(Δx,Δy) – бесконечно малое более высокого порядка, чем расстояние:

Если функция дифференцируема в точке, то ее полное приращение в этой точке состоит из двух частей :

1. Главной части приращения функции A∙Δx+B∙Δy – линейное относительно Δx,Δy

2. И нелинейное ω(Δx,Δy) – бесконечно малое более высокого порядка, чем главная часть приращения.

Главная часть приращения функции – линейная относительно Δx,Δy называется полным дифференциалом этой функции и обозначается: Δz = A∙Δx+B∙Δy, Δx=dx и Δy=dy или полный дифференциал функции двух переменных:

Достаточные условия дифференцируемости.

Теорема 1:

Если функция Z=f(x,y) дифференцируема в точке P(x,y), то она имеет в точке Р первые частные производные:

Теорема 2:

Если же частные производные непрерывны в окрестности точки Р, то эта функция дифференцируема, т.е существует дифференциал.