25. Предел функции в точке и на бесконечности.
y=f(x) определена некоторой областью Д, рассмотрим понятие придела функции в точке х0.
Определение1(по
гейне):
Число А наз. приделом функции f(x)
в точку х0, если ф-ция f(x)
определена в некоторой проколотой
окрестности точки х0 и для любой
последующей х(н-ое) при х(н)→х0
, когда н→∞
и х(н) не равно х0 последовательности
соответствует значение функции и
сводится к числу а. Обозначается
.
Замечание. Проколотой окрестностью точки х0 называется любая окрестность второй точки, то есть симметричный интервал, исключающий саму точку.
определение 2(по коши): Число наз. приделом функции у= f(x), если для любого сколь угодно малого числа Е(эпсилон)>0 найдется такое число а, зависящее от Е>0 что для всех х, для которых выполняется неравенство |x-x0|<a(x неравно а) следует что любое х-а<Е.
замечание: Число а выбирается индивидуально для каждой точки х0 и для каждого Е.
Определение 3(геометрическая интерпретация определения по коши): Число а предел ф-ции y=f(x) в точке х0, если функция y=f(x) определена в некоторой проколотой окрестности точки х0 и для любой Е окрестности точки а существует проколотая дельта х окрестности точки х0, такая что как только аргумент х0 принадлежит этой проколотой дельта-окрестности значение функции попадает в Е окрестность точки а.
замечание:все три данные определения эквивалентны и это доказуемо.
Не всякая функция имеет придел в точкех0=0. по определениям придел это число, функция у=Lnx при х→0, стремится к ∞ таким образом относительо придела функции возможны случаи:
1.функция имеет придел в точке это число.2.функция придела не имеет (1.функция является бесконечно большой в этой точке. 2. не определен вообще)
26. Свойство функции, имеющих придел.
теор.1. если функция имеет придел в точке то он единственный.
теор.2.если функция имеет придел в точке то она огроничена некоторой проколотой окрестностью этой точки.
теор.3.если функция y=f(x)имеет придел а в точке х0 то существует проколотая окрестность точки в кот. функция имеет знак, совподающий со знаком придела а, а неравно 0.
теор.4.если
и в некоторой проколотой окрестности
х0 для любых х имеет место неравенство
f1(x)≤f(x)≤f2(x)
тогда
.
теор.5.пусть функции f(x)и g(x) имеют придел в точке х0 тогда справедливы формулы:
Замечание1:формулы суммы и произведения(2,3) обобщаются на любое конечное число множителей, если использовать их для бесконечного кол-ва множеьелей то может возникнуть ошибка.
Замечание2: Как в результате применения формул (1-4) возникла неопределенность, то сперва нужно от неё избавится для получения однозначного результата.
27.Замечательные пределы
Замечательные пределы — термин, использующийся для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:
Первый замечательный предел:
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере, при условии стремления этой дуги к нулю.
Из геометрических соображений имеем SDOAС< SOAC < SDOBC.
Замечание. Если х < 0, то знаки неравенств изменяются на противоположные, выводы же остаются прежними.
Второй замечательный предел: Доказательство. Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞.
С ростом
основание степени уменьшается до
единицы, а показатель растет до
бесконечности, поэтому ничего конкретного
о поведении
сказать нельзя. Для вычисления
можно воспользоваться выражением для
бинома Ньютона:
Из
полученного выражения следует, что с
увеличением
величина
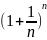растет.
Докажем
теперь, что данная последовательность
ограничена сверху. Заменим все скобки
вида
единицей. Так как
,
то
.
В
правой части неравенства после цифры
2 стоит убывающая геометрическая
прогрессия. Как известно, сумма
первых членов такой прогрессии равна:
.
В
нашем случае
.
С ростом n величина
будет, очевидно, стремится к единице.
Значит,
,
то есть, ограничено сверху.
Итак,
мы получили, что
.
Но так как
монотонно
возрастающая последовательность
ограниченная сверху, то она имеет
предел:
Можно
доказать, что данный предел справедлив
не только для натуральных чисел, но и
для любых значений
:
Полученное выражение и называется вторым замечательным пределом.
Число
используется для введения натуральных
логарифмов. Такие логарифмы обозначаются
,
при этом
.