Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Волгоградская государственная академия физической культуры»

«Утверждаю»

Зав. кафедрой ЕНДиИТ

__________Балакши Т.М.

« ___»________________2011г.

Кафедра ЕНДиИТ

Стеценко Н.В.

Лекции по курсу

Естественнонаучные основы физической культуры:

математика и физика

для студентов I курса очной формы обучения

направления подготовки

034300.62 «Физическая культура»

профилей подготовки

«Спортивная тренировка в избранном виде спорта» 

«Физкультурное образование»

«Спортивный менеджмент»

Лекция 1. Тема: Аналитическая геометрия на плоскости (2 часа)

Основные положения: Уравнение линии на плоскости, различные уравнения прямой на плоскости, условия параллельности и перпендикулярности двух прямых на плоскости, угол между двумя прямыми на плоскости, кривые 2-го порядка, их основные свойства.

План:

1. Уравнение линии на плоскости

2. Прямая линия. Различные уравнения прямой

2.1. Уравнение прямой, проходящей через данную точку, параллельно данному вектору

2.2. Уравнение прямой, проходящей через две данные точки

2.3. Уравнение прямой в отрезках

2.4. Уравнение прямой с угловым коэффициентом

2.5. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

2.6. Общее уравнение прямой

3. Взаимное расположение прямых

3.1. Угол между двумя прямыми

3.2. Условие параллельности прямых

3.3. Условие перпендикулярности прямых

4. Кривые второго порядка

4.1. Окружность

4.2. Эллипс

4.3. Гипербола

4.4. Парабола

Вопросы для самопроверки:

1. Напишите формулу для вычисления угла между двумя прямыми.

2. Как выглядит условие параллельности и перпендикулярности двух прямых?

3. Как выглядит уравнение высоты в треугольнике, если известны координаты его вершин?

4. Сформулируйте определение окружности, эллипса, гиперболы, параболы. Каковы канонические уравнения этих линий?

5. Что называется эксцентриситетом эллипса, гиперболы?

Лекция 2. Тема: Дифференцирование функций (2 часа)

Основные положения: понятия функции, предела функции, производной функции, геометрический смысл производной, механический смысл производной, производные высших порядков, производная сложной функции, правила дифференцирования, дифференциал функции, применение производной к исследованию функции.

План:

1. Понятие функциональной зависимости и способы ее представления

2. Предел функции

2.1. Числовая последовательность. Предел числовой последовательности

2.2. Предел функции в точке

3. Бесконечно малые функции и их свойства

4. Бесконечно большие функции и их связь с бесконечно малыми

5. Теоремы о действиях над пределами

6. Приращение аргумента и приращение функции

7. Понятие производной функции

8. Геометрический смысл производной

9. Механический смысл производной

10. Правила дифференцирования

11. Таблица производных элементарных функций

12. Производные высших порядков

13. Дифференциал функции

14. Применение дифференциального исчисления к исследованию функций

14.1. Возрастание и убывание функции

14.2. Экстремум функции

14.3. Наибольшее и наименьшее значение функции на отрезке

14.4. Выпуклость, вогнутость функции

14.5. Точки перегиба функции

15. Задачи на нахождение наименьших и наибольших значений величин

Вопросы для самопроверки:

1. Дайте понятие функциональной зависимости. Приведите примеры такой зависимости из области ФК.

2. Перечислите способы представления функциональной зависимости.

3. Сформулируйте определение производной.

4. Каков геометрический смысл производной?

5. В чем заключается механический смысл производной?

6. Каковы правила вычисления производных от суммы, произведения, частного двух функций?

7. Сформулируйте правило вычисления производной сложной функции.

8. Чем отличается дифференциал функции от ее приращения?

9. Каковы признаки возрастания и убывания функции?

10. Сформулируйте правила нахождения экстремумов функции.

11. Приведите пример, показывающий, что обращение в нуль производной не является достаточным условием экстремума функции.

12. Как найти интервалы выпуклости, вогнутости, точки перегиба кривой?

Лекция 3. Тема: Интегрирование функций (2 часа)

Основные положения: понятие неопределенного интеграла, основные методы интегрирования, понятие определенного интеграла, формула Ньютона – Лейбница, приложение определенного интеграла к вычислению площадей плоских фигур и объемов тел вращения.

План:

1. Неопределенный интеграл и его свойства

2. Таблица основных интегралов

3. Основные методы интегрирования

3.1. Непосредственное интегрирование

3.2. Метод замены переменной

3.3. Метод интегрирования по частям

4. Понятие определенного интеграла. Свойства определенного интеграла

5. Вычисление определенных интегралов. Формула Ньютона-Лейбница

6. Приложение определенного интеграла

6.1. Вычисление площадей плоских фигур

6.2. Вычисление объемов тел вращения относительно оси OX и оси OY

6.3. Вычисление пути, пройденного точкой

Тема 1. Элементы аналитической геометрии на плоскости План:

1. Уравнение линии на плоскости

2. Прямая линия. Различные уравнения прямой

2.1. Уравнение прямой, проходящей через данную точку, параллельно данному вектору

2.2. Уравнение прямой, проходящей через две данные точки

2.3. Уравнение прямой в отрезках

2.4. Уравнение прямой с угловым коэффициентом

2.5. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

2.6. Общее уравнение прямой

3. Взаимное расположение прямых

3.1. Угол между двумя прямыми

3.2. Условие параллельности прямых

3.3. Условие перпендикулярности прямых

4. Расстояние от точки до прямой

5. Кривые второго порядка

5.1. Эллипс

5.2. Гипербола

5.3. Парабола

§1. Уравнение линии на плоскости

Линии на плоскости рассматриваются как геометрические места точек, их составляющих.

Введение на плоскости системы координат позволяет положение точек плоскости однозначно определять заданием пар действительных чисел – их координат, а положение линий на плоскости определять с помощью равенств, связывающих пары чисел – координаты точек этих линий, то есть с помощью уравнений.

Определение. Уравнение называется уравнением линии L, если координаты любой точки линии удовлетворяют этому уравнению, а координаты точек, не принадлежащих линии L, этому уравнению не удовлетворяют.

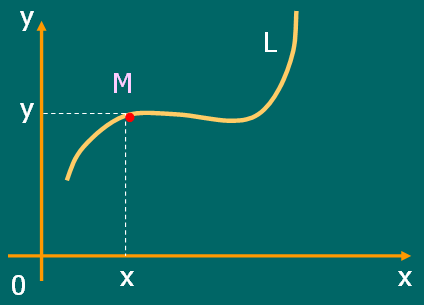
Введение на плоскости системы координат позволяет изучение геометрических свойств линий заменить исследованием соответствующих им уравнений.

§2. Прямая линия. Различные уравнения прямой

2.1. Уравнение прямой, проходящей через данную точку, параллельно данному вектору

Проведем прямую через данную точку М(x₀;y₀), параллельно данному вектору .

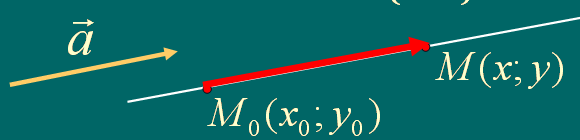
Возьмем на прямой произвольную точку М(x;y), тогда векторы и - коллинеарны и их координаты пропорциональны. Так как

и , то получим:

- уравнение прямой, проходящей через данную точку, параллельно данному вектору.

2.2. Уравнение прямой, проходящей через две данные точки

Проведем прямую через две данные точки М₁(x₁;y₁) и М₂(x₂;y₂).

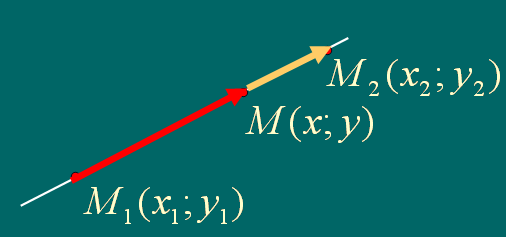
Возьмем произвольную точку М(x;y) на прямой, тогда векторы и - коллинеарны и их координаты пропорциональны.

Так как , , то получим:

- уравнение прямой, проходящей через две данные точки.

2.3. Уравнение прямой в отрезках

Пусть прямая отсекает на осях координат соответственно отрезки и .

Можно считать, что прямая проходит через две данные точки и и по пункту 2.2. имеем:

- уравнение прямой в отрезках.

2.4. Уравнение прямой с угловым коэффициентом

Рассмотрим уравнение прямой из пункта 2.1.:

. Обозначим .

- уравнение прямой, проходящей через данную точку с угловым коэффициентом k.

Если в качестве М₀ возьмем точку с координатами (0;b), то есть точку пересечения прямой с осью OY, то получим:

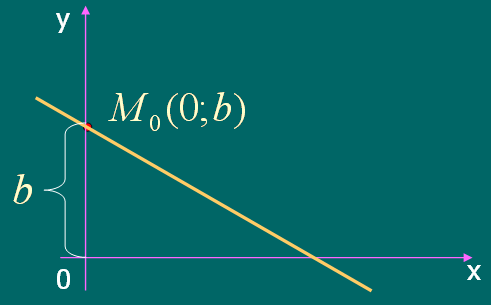
- уравнение прямой с угловым коэффициентом.

2.5. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Проведем прямую через данную точку М₀(x₀;y₀) перпендикулярно данному вектору . Возьмем на прямой произвольную точку М(x;y) и рассмотрим вектор .

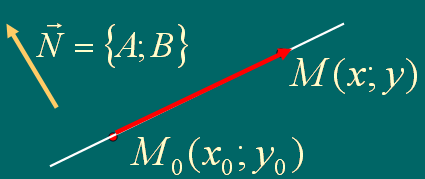
Вектор и взаимно перпендикулярны ( ) и по условию перпендикулярности векторов получим:

- уравнение прямой проходящей, через данную точку перпендикулярно данному вектору.

2.6. Общее уравнение прямой

Рассмотрим предыдущее уравнение и раскроем скобки:

Обозначим , получим:

- общее уравнение прямой.

Замечание. При решении задач на составление уравнений прямых ответ принято записывать в виде общего уравнения или уравнения с угловым коэффициентом.

§3. Взаимное расположение прямых

3.1. Угол между двумя прямыми

Пусть прямые заданы уравнениями и , - угол между прямыми. Известно, что , и (по теореме о внешнем угле треугольника).

Тогда

- угол между двумя прямыми.

3.2. Условие параллельности прямых

Если прямые параллельны, то и или .

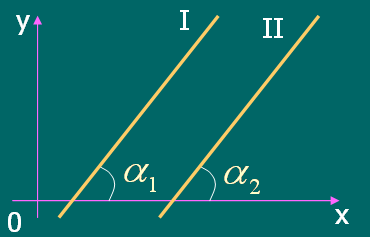
- условие параллельности двух прямых.

3.3. Условие перпендикулярности прямых

Если прямые перпендикулярны, то . не существует, а это случится тогда, когда 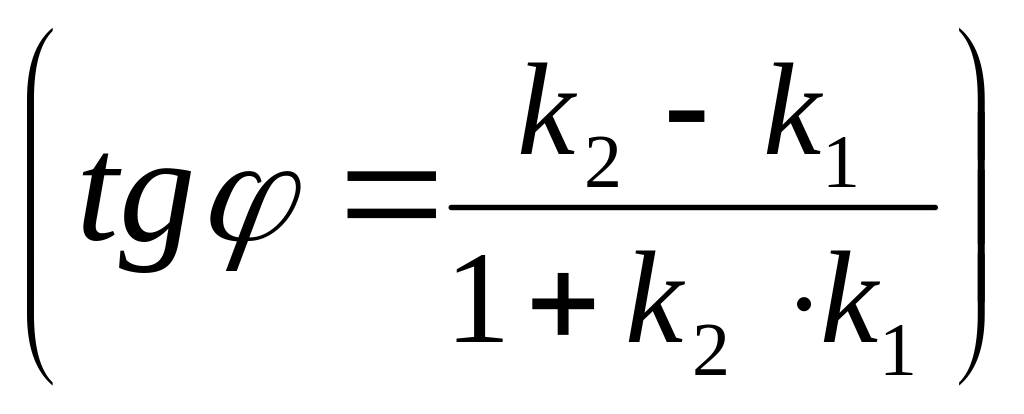или

- условие перпендикулярности двух прямых.

Замечание. Если прямые заданы общими уравнениями

, , то

- условие параллельности двух прямых.

- условие перпендикулярности двух прямых.