- •Тема 1. Элементы аналитической геометрии на плоскости План:
- •§4. Расстояние от точки до прямой
- •§5. Кривые второго порядка
- •5.1. Окружность
- •5.2. Эллипс
- •Свойства эллипса
- •5.3. Гипербола
- •Свойства гиперболы
- •5.4. Парабола
- •Свойства параболы
- •Тема 3. Дифференцирование функций План:
- •§2. Предел функции
- •2.1. Числовая последовательность. Предел числовой последовательности
- •2.2. Предел функции в точке
- •§7. Понятие производной функции
- •14.3. Наибольшее и наименьшее значение функции на отрезке
- •14.4. Выпуклость, вогнутость функции
- •14.5. Точки перегиба функции
- •§15. Задачи на нахождение наименьших и наибольших значений величин
- •Тема 3. Интегрирование функций
- •§1. Неопределенный интеграл и его свойства
- •§2. Таблица основных интегралов
- •§3. Основные методы интегрирования
- •3.1. Непосредственное интегрирование
- •3.2. Метод замены переменной
- •3.3. Интегрирование по частям
- •§4. Понятие определенного интеграла. Свойства определенного интеграла
- •§5. Вычисление определенных интегралов. Формула Ньютона-Лейбница
- •§6. Приложение определенного интеграла
- •6.1. Вычисление площадей плоских фигур
- •6.2. Вычисление объемов тел вращения относительно оси ox и оси oy
- •6.3. Вычисление пути, пройденного точкой
- •Тема 5: Элементы теории вероятностей План:
- •§1. Некоторые формулы комбинаторики
- •§2. Предмет теории вероятностей. Основные определения
- •§3. Классическое определение вероятности
- •§4. Основные теоремы о вычислении вероятностей сложных событий
- •4.1. Теорема сложения вероятностей несовместных событий
- •4.2. Теорема умножения вероятностей независимых событий
- •4.3. Теорема умножения вероятностей зависимых событий
- •4.4. Теорема сложения вероятностей совместных событий
- •§5. Формула полной вероятности
- •Тема 5: основы математической статистики План:
- •§1. Случайные величины
- •§2. Основные понятия математической статистики
- •§3. Группировка данных
- •3.1. Группировка данных в случае количественного дискретного признака (построение дискретного вариационного ряда)
- •5.2. Группировка данных в случае количественного непрерывного признака (построение интервального вариационного ряда)
- •§4. Статистические характеристики
- •4.1. Средние характеристики
- •4.2. Характеристики вариации
- •Тема 6. Проверка статистических гипотез и оценка параметров План:
- •§1. Проверка статистических гипотез
- •§2. Критерий согласия Пирсона
- •§3. Оценка параметров генеральной совокупности
- •3.1. Оценка средней арифметической генеральной совокупности
- •3.2. Оценка дисперсии генеральной совокупности
- •Тема 7. Элементы корреляционного и регрессионного
- •§1. Функциональная и корреляционная взаимосвязи
- •§2. Корреляционное поле. Коэффициент корреляции
- •§3. Расчет коэффициента корреляции методом условных вариант
- •§4. Ошибка коэффициента корреляции
- •§5. Регрессионный анализ
§7. Понятие производной функции
Пусть функция
y=f(x)
определена
на некотором множестве X.
Возьмем точку
![]() и произвольную точку
и произвольную точку
![]() .
Разность x-x0
называется приращением
аргумента и
обозначается
.
Разность x-x0
называется приращением
аргумента и
обозначается
![]() ,
то есть
,
то есть
![]() .
.
Разность f(x)-f(x0)
называется приращением
функции и
обозначается
![]() ,
то есть
,
то есть
![]() или
или
![]() .
.
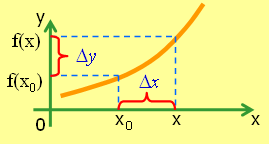
Если
![]() и
- соответственно приращения аргумента
и функции, то отношение
и
- соответственно приращения аргумента
и функции, то отношение
![]() выражает среднюю скорость изменения
функции при изменении аргумента от
значения x0
до
выражает среднюю скорость изменения
функции при изменении аргумента от
значения x0
до
![]() .
Когда
.
Когда
![]() ,
то предел, к которому стремится отношение
,
если он существует, представляет скорость
изменения функции для данного значения
аргумента x0.
,
то предел, к которому стремится отношение
,
если он существует, представляет скорость
изменения функции для данного значения
аргумента x0.
Определение Предел отношения при называется производной функции в точке и обозначается:
![]() .
.
Замечание. Операция взятия производной называется дифференцированием.
§8. Геометрический смысл производной
Пусть y=f(x) непрерывна на D(f). Построим график функции и возьмем на полученной кривой точку М0(x0;y0).
Проведем касательную к графику функции в точке М0, тогда: производная функции f(x) в точке x0 есть угловой коэффициент касательной к графику функции в точке М0(x0;y0).
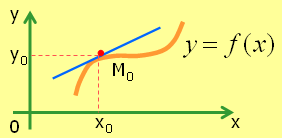
Уравнение касательной к графику функции в точке М0(x0;y0) имеет вид:
![]()
§9. Механический смысл производной
§10. Правила дифференцирования
Пусть u=u(x)
и v=v(x)
имеют производные в точке
соответственно равны
![]() и
и
![]() ,
тогда:
,
тогда:
1. (u ± v)=u±v.
2. (uv)=uv + uv.
3. .
4. (Cu)=Cu , где C=const.
5. Пусть
![]() ,
где u,
в свою очередь, есть функция от аргумента
,
где u,
в свою очередь, есть функция от аргумента
![]() :
:
![]() ,
тогда
,
тогда
![]() .
.
§11. Таблица производных элементарных функций
1.
![]() ,
C=const
8.
,
C=const
8.
![]()
2.
![]() 9.
9.
![]()
3.
![]() 10.
10.
![]()
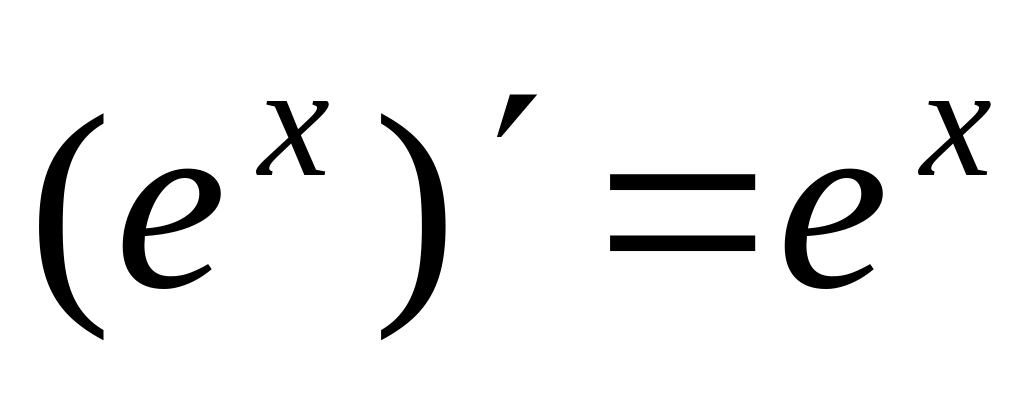 11.
11.
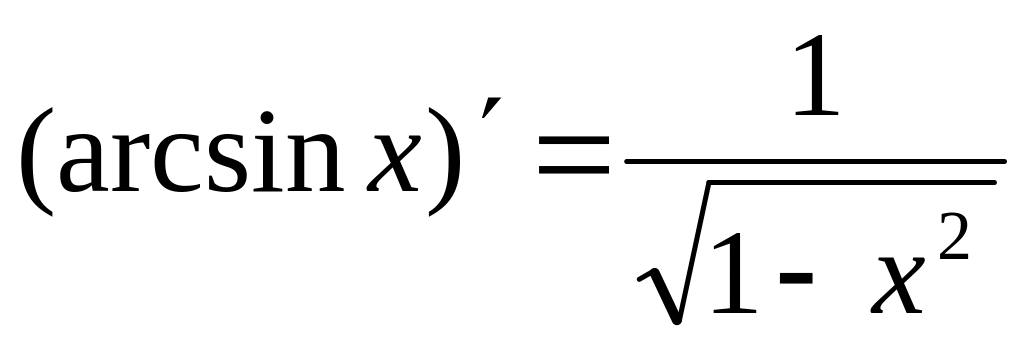
5.
![]() 12.
12.
![]()
6.
![]() 13.
13.
![]()
7.
![]() 14.
14.
![]()
§12. Производные высших порядков
Под производной
n-го
порядка будем понимать производную от
производной (n-1)-го
порядка, то есть
![]() или
или
![]() .
.
§13. Дифференциал функции
Определение
Дифференциалом
функции f(x)
в точке x
называется линейная относительно
часть приращения функции
![]() (или
(или
![]() ).
).
Обозначают:
![]()
Замечание.
Дифференциал аргумента равен его
приращению, то есть
![]() .
Следовательно,
.
Следовательно,
![]() - дифференциал
функции в данной точке равен произведению
ее производной в этой точке на дифференциал
аргумента.
- дифференциал
функции в данной точке равен произведению
ее производной в этой точке на дифференциал
аргумента.
§14. Применение дифференциального исчисления к исследованию функций
14.1. Возрастание и убывание функции
По первой производной можно решить вопрос о возрастании и убывании функции.
Рассмотрим функцию y=f(x), определенную и дифференцируемую на интервале (a;b).
Если производная f(x) на интервале (a;b) положительна f(x)>0, то функция f(x) возрастает на интервале (a;b), если производная f(x) отрицательна [ f(x)<0], то функция f(x) убывает на интервале (a;b) .
14.2. Экстремум функции
В точках, где производная обращается в 0, то есть y=0, функция может иметь максимум или минимум.
Функция y=f(x) имеет максимум в точке x=x1, если можно найти такую окрестность точки x1, в которой при всех x ≠ x1 выполняется неравенство: f(x)<f(x1).
Функция y=f(x) имеет минимум в точке x=x2, если можно найти такую окрестность точки x2, в которой при всех x ≠ x2 выполняется неравенство: f(x)<f(x2).
Пусть для функции y=f(x) y обращается в 0 в точке x0.
Если при переходе через эту точку y меняет знак с «+» на «-», то x0 - точка максимума, если y меняет знак с «-» на «+», то x0 - точка минимума.