
- •Тема 1. Матрицы и определители
- •Матрицы.
- •1.2.2. Свойства операций сложения (вычитания) матриц:
- •1.2.3. Умножение матрицы на число.
- •1.3. Умножение матриц.
- •1.3.3. Пример.
- •1.4.10.Свойства определителей.
- •1.5. Обратная матрица.
- •1.6.3. Элементарными преобразованиями над матрицей называются преобразования вида:
- •Тема 2. Системы линейных уравнений. (Лекции№3-4)
- •Основные определения.
- •2.3. Совместность систем алгебраических уравнений.
- •Матричный способ решения систем линейных алгебраических уравнений.
- •2.5. Решение систем линейных уравнений методом Гаусса.
- •2.5.3. Последовательность элементарных преобразований расширенной матрицы системы.
- •Решение однородных систем линейных уравнений.
- •Решение систем однородных линейных уравнений:
- •Контрольное домашнее задание №3. Тема: Системы линейных уравнений.
- •Тема 3. Векторная алгебра. (Лекции№5-6)
- •3.1. Общие определения
- •3.2. Линейные операции над векторами.
- •3.3. Действия над векторами в координатной форме
- •3.4. Базис на плоскости и в пространстве.
- •3.4.1. Линейная зависимость и независимость векторов.
- •3.4.4. Выводы:
- •3.4.11. Расстояние между двумя точками в пространстве.
- •3.4.12. Деление отрезка в заданном отношении.
- •3.5. Скалярное произведение векторов.
- •3.5.2. Свойства скалярного произведения:
- •3.6. Векторное произведение двух векторов.
- •3.7. Смешанное произведение трех векторов.
- •3.8. Практическое занятие№4. «Нелинейные операции с векторами»
3.4. Базис на плоскости и в пространстве.
3.4.1. Линейная зависимость и независимость векторов.
Вектор С=123 называется линейной комбинацией или системой векторов А, В и К, а числа 1, 2, и 3 коэффициентами линейной комбинации.
3.4.2. Векторы А, В и К называются линейно независимыми, если их линейная комбинация равна нулю только, когда все коэффициенты равны нулю.
3.4.3. Векторы А, В и К называются линейно зависимыми, если их линейная комбинация равна нулю не только, когда все коэффициенты равны нулю, но и тогда, когда среди чисел 1, 2, и 3 есть хотя бы одно не равное нулю.
Если векторы линейно зависимы, то хотя бы один из них может быть выражен как линейная комбинация остальных, например, =(23)1.
3.4.4. Выводы:
система векторов может быть либо линейно независимой, либо линейно зависимой,
если часть системы векторов линейно зависима, то и вся система линейно зависима,
если система векторов линейно независима, то и любая ее часть линейно независима. 3.4.5. Геометрическая интерпретация линейной зависимости векторов:
Два ненулевых вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Три ненулевых вектора линейно зависимы тогда и только тогда, когда они компланарны, то есть лежат в одной плоскости.
3.4.6. Базисом называется упорядоченная совокупность линейно независимых векторов. На плоскости два любых неколлинеарных вектора образуют базис. В пространстве три любых некомпланарных вектора образуют базис. Все другие векторы на плоскости или в пространстве могут быть выражены через базисные. Базисом могут быть разные наборы векторов, но наиболее удобен и, поэтому широко распространен базис, образованный ортогональными векторами.
3.4.7. Прямоугольная система координат. Если базисные векторы попарно ортогональны и длина каждого их них равна 1 , то такой базис называется ортонормированным. На основе такого базиса строится Декартова прямоугольная система координат (рис.6): на плоскости ОХУ, где i и j единичные векторы (орты) по оси абсцисс (OX) и оси ординат (OY) соответственно, i j , i = j =1 и в проcтранстве – ОXУZ, где i , j и единичные векторы (орты) по осям абсцисс (OX), ординат (OY) и аппликат (OZ) соответственно, i j , i , j , i = j =1.

 z
z
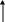 y
y

 j
i
x
y
j
i
x
y



 o
o
x
Рис 6. Базис на плоскости. Рис.7. Базис в пространстве.
3.4.8. Координаты вектора в прямоугольной системе равны проекциям вектора на соответствующие оси. Приведем очень важные свойства проекций вектора на ось:
* При умножении вектора на число его проекции умножаются на то же число.
* Проекция суммы векторов на ось равна сумме проекций этих векторов.
* Проекция вектора на ось координат равна разности координат его конца и начала.
3.4.9.
Пример. Зная,
что
![]() ,
определить координаты векторов:
,
определить координаты векторов:
![]() .
Решение.
Найдем
координаты векторов
.
Решение.
Найдем
координаты векторов
![]() и p:
и p:
![]() Ответ.
Ответ.
![]() .
.
3.4.10. Пример. Найти вектор А=2В–3С, если В= 4i +5j , С=3i–6 j.
Решение. A=2(4i +5j)–3( 3i–6 j)=–8i+10j–9i+18j=–i+28j.
