2.3. Совместность систем алгебраических уравнений.

2.3.1. Расширенной матрицей системы алгебраических уравнений называется матрица А⁺, полученная из матрицы системы А добавлением к ней столбца свободных членов.

. (9)

2.3.2. Теорема Кронекера–Капелли. Для того, чтобы система уравнений была совместна необходимо и достаточно, чтобы ранг матрицы системы А равнялся рангу расширенной матрицы А⁺, то есть r (A)=r (A⁺).

Следствия:

1) Если r(A)  r(A⁺), то система несовместна и решений не имеет.

2) Если r(A) = r(A⁺)=n, то при ранге матрицы равном числу неизвестных решение единственное.

3) Если r(A) = r(A⁺), то при ранге меньшем числа переменных (rn) решений бесчисленное множество, при этом (n–r) переменным можно придать произвольные значения, а оставшиеся r переменных единственным образом выразить через них.

4. Матричный способ решения систем линейных алгебраических уравнений.

1. Линейная система уравнений в матричной форме. Возьмем систему линейных уравнений

. (10)

Введем следующие обозначения: А– матрица системы, Х –матрица-столбец неизвестных, С– матрица-столбец свободных членов.

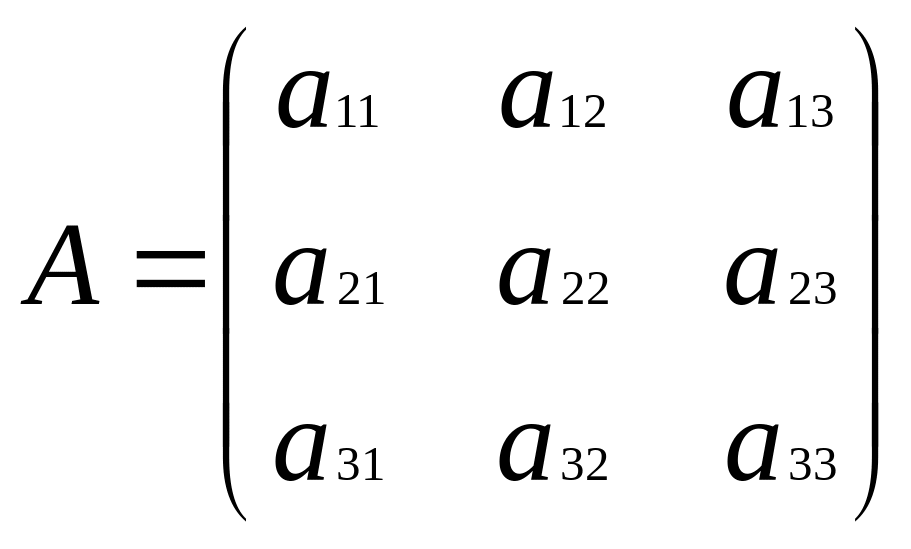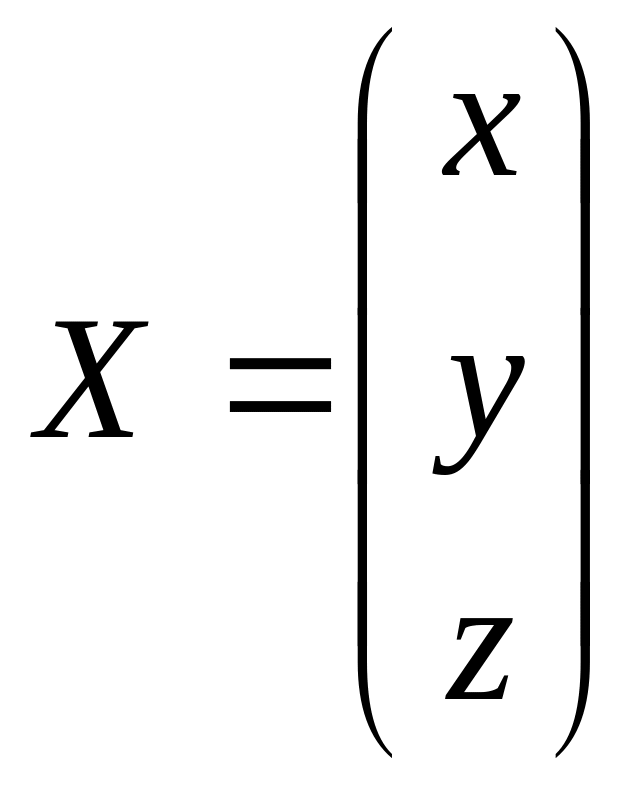, и .

Легко заметить, что при умножении матрицы А на Х получается матрица С, то есть мы получили в компактной форме матричное уравнение: АХ=С. (14)

Итак, линейная система (10) эквивалентна матричному уравнению (11). Найдем матрицу неизвестных. Для этого надо решить матричное уравнение(11). Если А – неособенная матрица, то умножив это уравнение слева и справа на А^-1, получим А^-1АХ=А^-1С. Известно, что А^-1АХ= ЕХ=Х= А^-1С, учитывая это получаем формулу для решения системы линейных уравнений матричным способом:

Х= А^-1С. (12)

Матрица неизвестных определяется как произведение обратной матрицы системы на матрицу свободных членов.

Замечание. Напомним, что обратная матрица существует только у тех матриц, у которых определитель не равен нулю.

2.4.2. Пример. Решить систему уравнений матричным способом: .

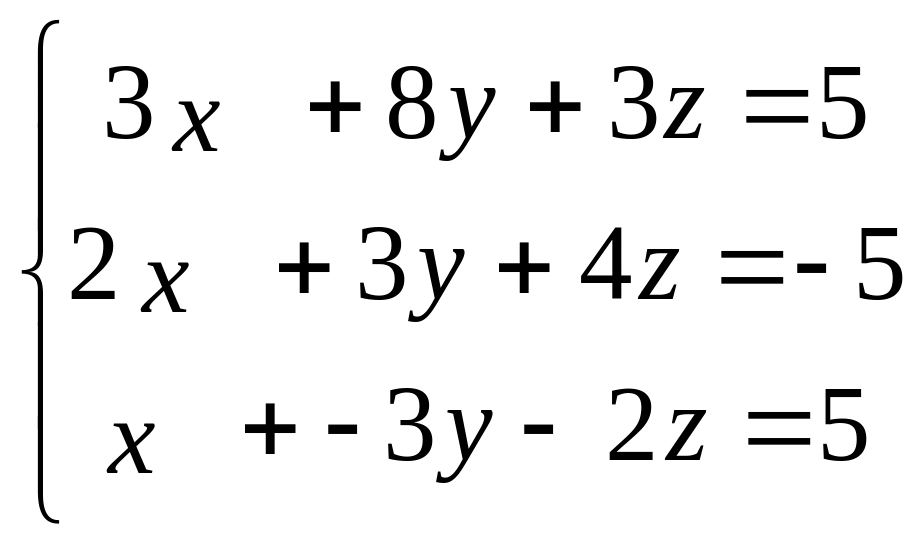Решение.

1) Вычислять определитель сиcтемы нам не надо, так как в параграфе 2.2. при решении этой системы по формулам Крамера мы получили А=550.

2) Вычисляем алгебраические дополнения и обратную матрицу:

А₁₁=6. А₁₂=8, А₁₃= –9, А₂₁=7, А₂₂= –9, А₂₃=17, А₃₁=23, А₃₂= –6, А₃₃= –7.

.

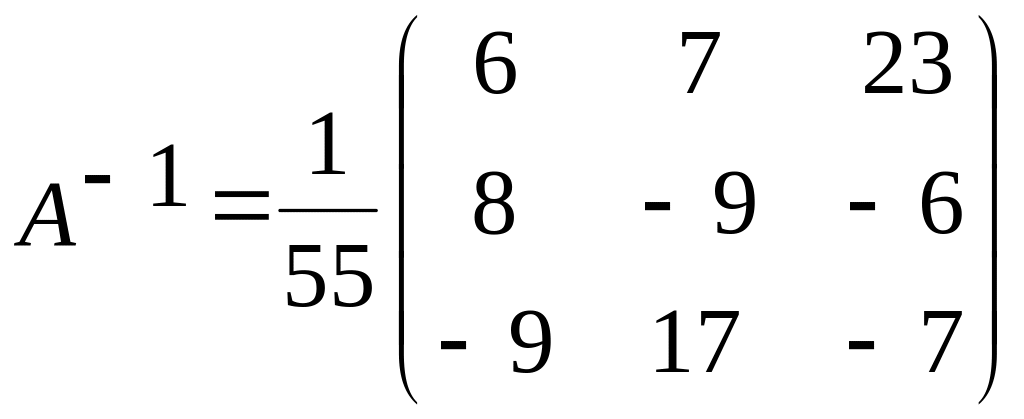3) Находим решение системы уравнений:

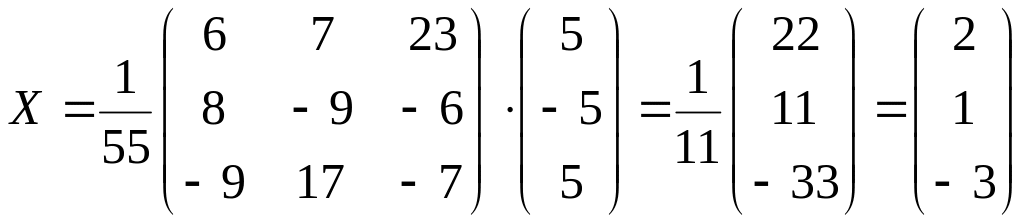. Ответ. (2, 1, –3).

2.4.3. Пример. Обувная фабрика производит 3 вида продукции: кроссовки, ботинки и туфли. Используется сырье 3 типов. Нормы расхода сырья на одну пару обуви и объем расхода за 1 день работы приведены в таблице.

Вид сырья	Расход на 1 пару усл.ед.) Кроссовки	Расход на 1 пару ботинки	Расход на 1 пару(усл.ед) туфли	Суммарный расход сырья за 1 день
S1	3	5	4	2000
S2	1	2	1	680
S3	2	3	2	1160

Найти объем выпуска продукции за 1 день.

Решение. Обозначим выпуск продукции каждого вида за 1 день , получим систему линейных алгебраических уравнений .

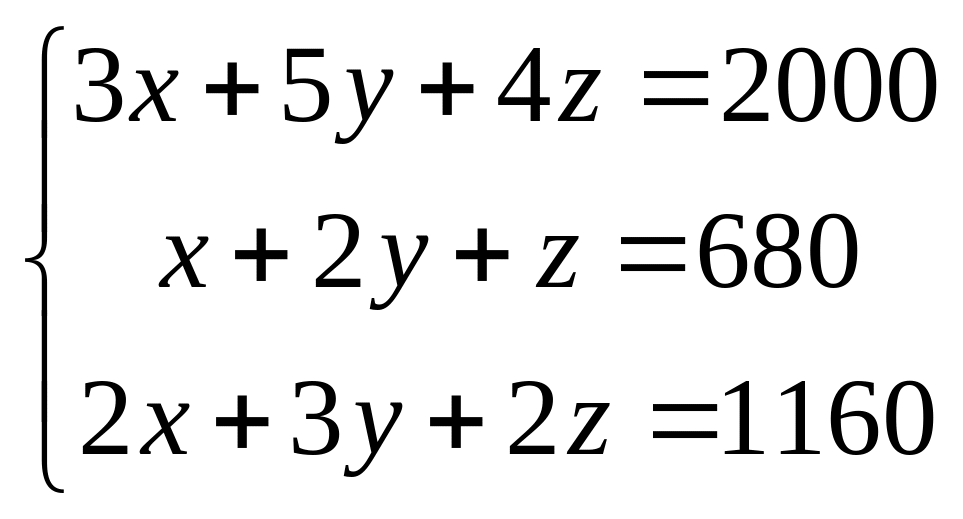Для ее решения используем метод обратной матрицы. Вычислим

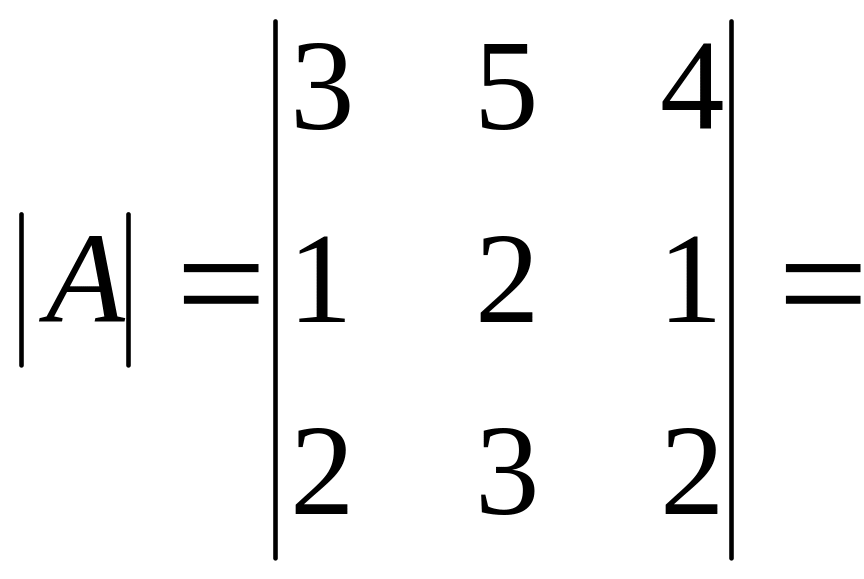–1, значит обратная матрица существует. Вычисляем алгебраические дополнения: А₁₁=1, А₁₂=0, А₁₃= –1, А₂₁=2, А₂₂= –2, А₂₃=1, А₃₁= –3, А₃₂=1, А₃₃= –1. Вычисляем обратную матрицу

и решаем матричное уравнение Х=А^–1В, где В= . Находим .

Ответ. За 1 день выпускается 120 пар кроссовок, 200 пар ботинок и 160 пар туфель.