
- •Тема 1. Матрицы и определители
- •Матрицы.
- •1.2.2. Свойства операций сложения (вычитания) матриц:
- •1.2.3. Умножение матрицы на число.
- •1.3. Умножение матриц.
- •1.3.3. Пример.
- •1.4.10.Свойства определителей.
- •1.5. Обратная матрица.
- •1.6.3. Элементарными преобразованиями над матрицей называются преобразования вида:
- •Тема 2. Системы линейных уравнений. (Лекции№3-4)
- •Основные определения.
- •2.3. Совместность систем алгебраических уравнений.
- •Матричный способ решения систем линейных алгебраических уравнений.
- •2.5. Решение систем линейных уравнений методом Гаусса.
- •2.5.3. Последовательность элементарных преобразований расширенной матрицы системы.
- •Решение однородных систем линейных уравнений.
- •Решение систем однородных линейных уравнений:
- •Контрольное домашнее задание №3. Тема: Системы линейных уравнений.
- •Тема 3. Векторная алгебра. (Лекции№5-6)
- •3.1. Общие определения
- •3.2. Линейные операции над векторами.
- •3.3. Действия над векторами в координатной форме
- •3.4. Базис на плоскости и в пространстве.
- •3.4.1. Линейная зависимость и независимость векторов.
- •3.4.4. Выводы:
- •3.4.11. Расстояние между двумя точками в пространстве.
- •3.4.12. Деление отрезка в заданном отношении.
- •3.5. Скалярное произведение векторов.
- •3.5.2. Свойства скалярного произведения:
- •3.6. Векторное произведение двух векторов.
- •3.7. Смешанное произведение трех векторов.
- •3.8. Практическое занятие№4. «Нелинейные операции с векторами»
1.6.3. Элементарными преобразованиями над матрицей называются преобразования вида:
*замена строк столбцами; *перестановка двух строк (столбцов); *умножение элементов строки (столбца) на одно и то же число, отличное от нуля; *прибавление к элементам строки (столбца) другой строки (столбца), умноженной на одно и то же число; *отбрасывание строк (столбцов), состоящих из одних нулей.
1.6.4.
Пример.
Вычислить ранг матрицы
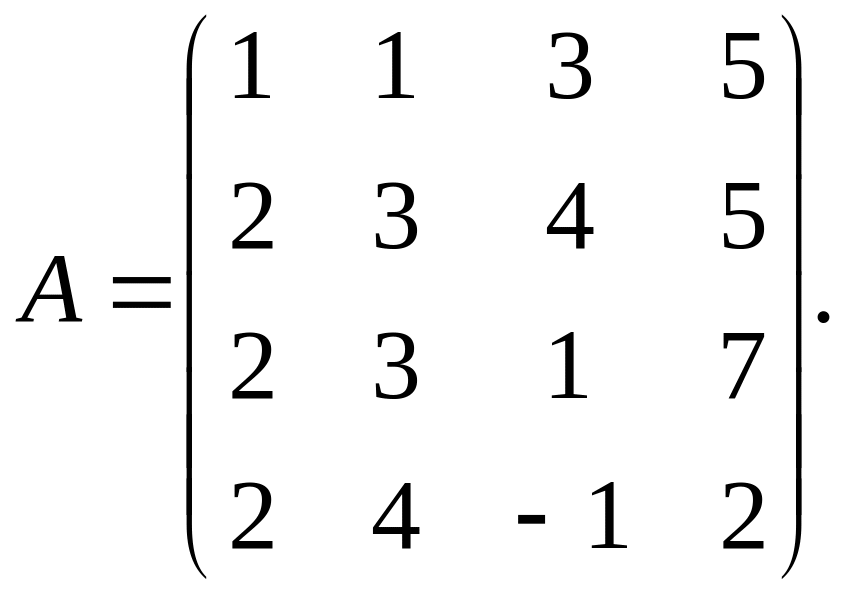 Решение.
Вычтем из второй, третьей и четвертой
строк первую, умноженную на 2, а затем
из третьей строки вычитаем вторую
Решение.
Вычтем из второй, третьей и четвертой
строк первую, умноженную на 2, а затем
из третьей строки вычитаем вторую
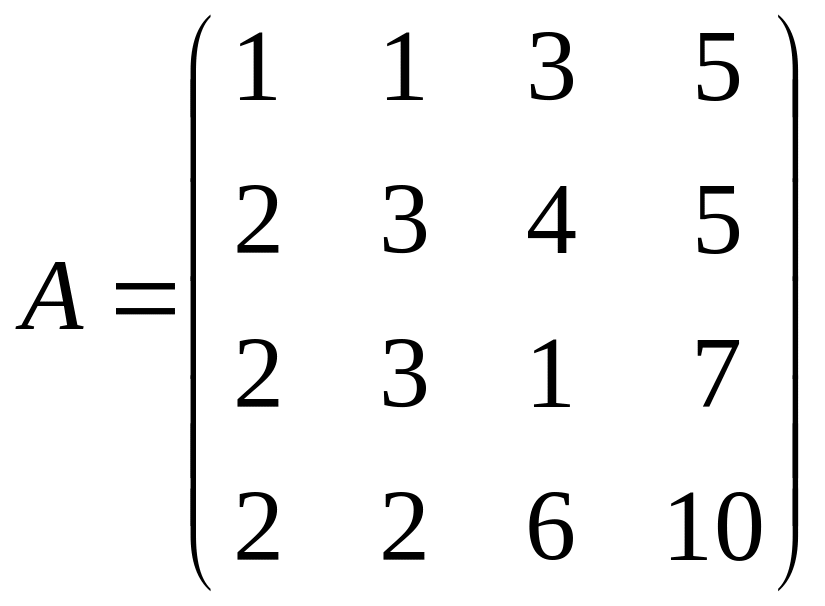
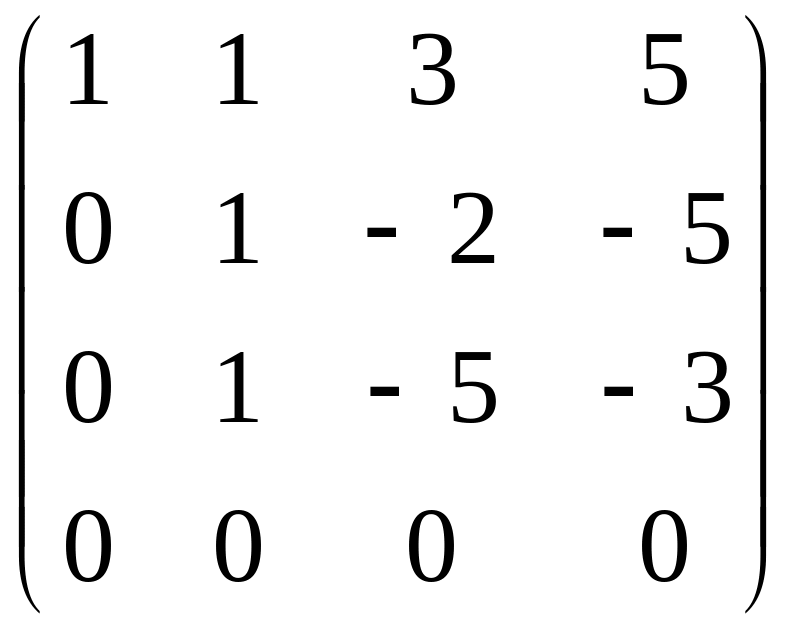
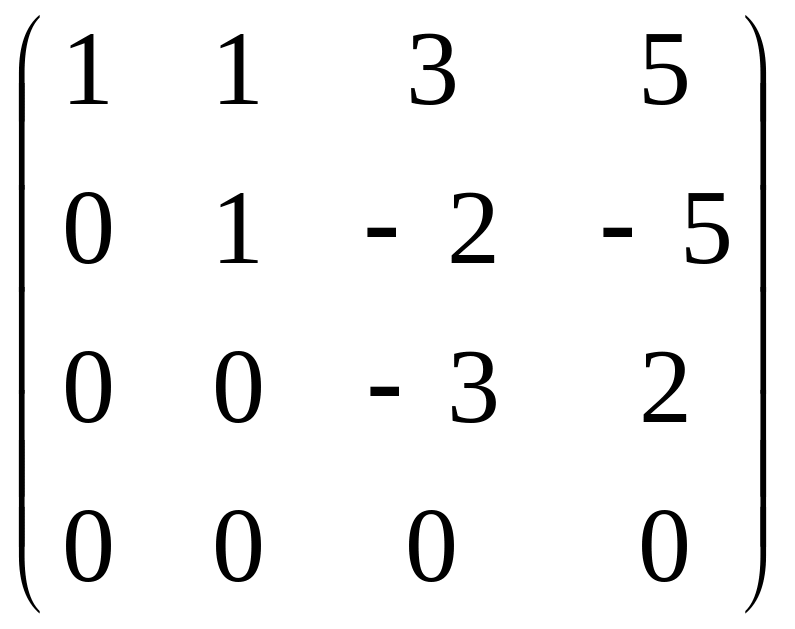 .
.
В результате в левом верхнем углу можем выделить минор размера три на три, не равный нулю. Следовательно, ранг матрицы равен трем, то есть r(A)=3.
Тема 2. Системы линейных уравнений. (Лекции№3-4)
Основные определения.
2.1.1. Система уравнений. Конечное множество уравнений, рассматриваемых совместно, называют системой уравнений. Пусть задана система трех линейных уравнений с тремя неизвестными:
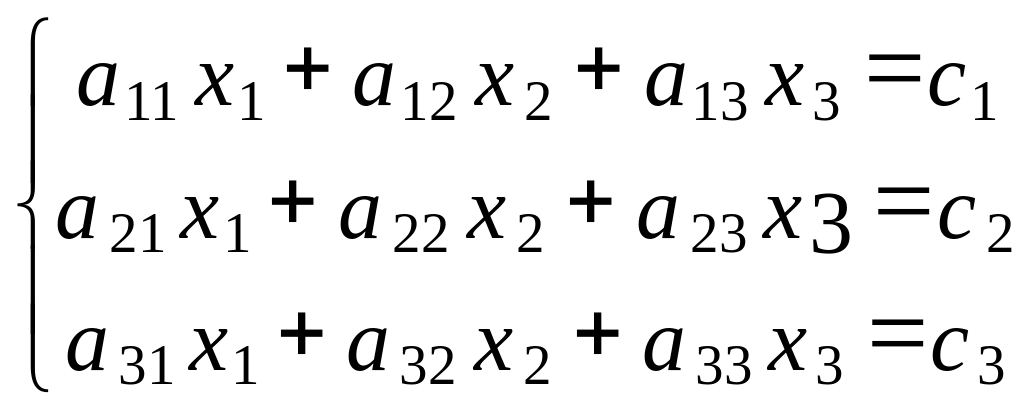 или
или
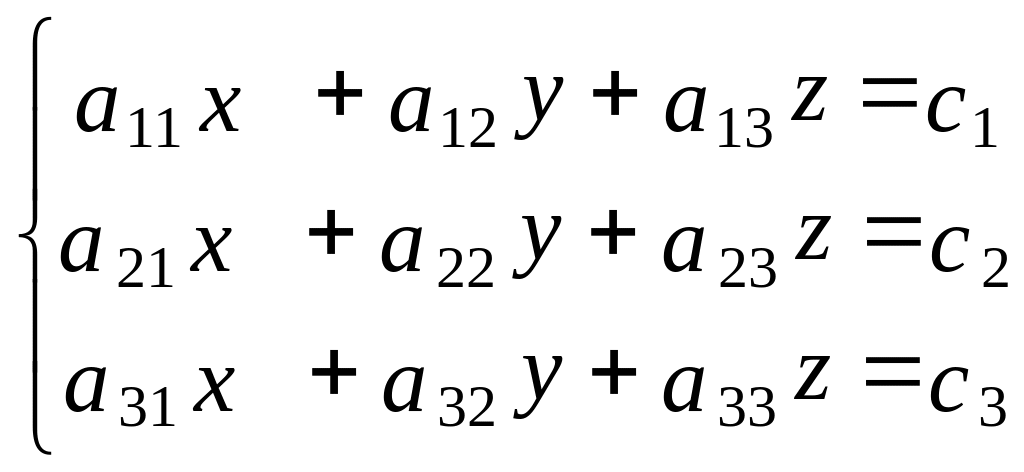 .
(7)
.
(7)
В первом варианте записи неизвестные пронумерованы, а во втором обозначены разными буквами. Коэффициенты при неизвестных обозначены одинаково: в индексе первая цифра номер уравнения, а вторая номер неизвестного. Индекс свободного члена ci обозначает номер уравнения.
2.1.2. Решением
системы линейных уравнений (7) с
неизвестными
![]() называется
множество значений неизвестных,
удовлетворяющих одновременно каждому
из уравнений заданной системы.
Система решена полностью, если найдены
все такие решения. Если система не имеет
решений, то говорят, что она противоречивая
или несовместная. Если все решения одной
системы являются решениями другой, то
вторую систему называют следствием
первой системы, а системы эквивалентными.
называется
множество значений неизвестных,
удовлетворяющих одновременно каждому
из уравнений заданной системы.
Система решена полностью, если найдены
все такие решения. Если система не имеет
решений, то говорят, что она противоречивая
или несовместная. Если все решения одной
системы являются решениями другой, то
вторую систему называют следствием
первой системы, а системы эквивалентными.
2.1.3. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
2.1.3. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет бесчисленное множество решений.
2.1.4. Множеством допустимых значений системы называют множество значений входящих в систему буквенных величин, при которых они имеют смысл. Приведем примеры системы трех линейных уравнений (первой степени) с тремя неизвестными и системы двух уравнений с двумя неизвестными:
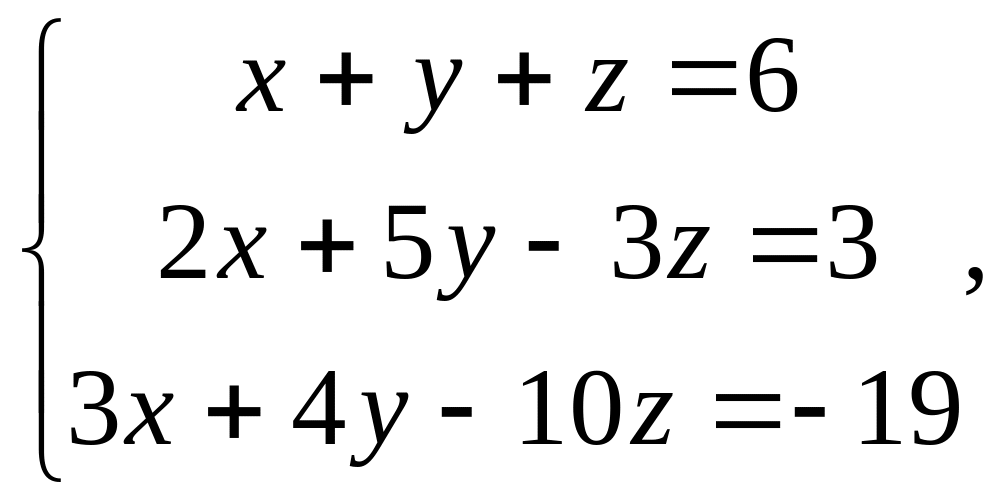
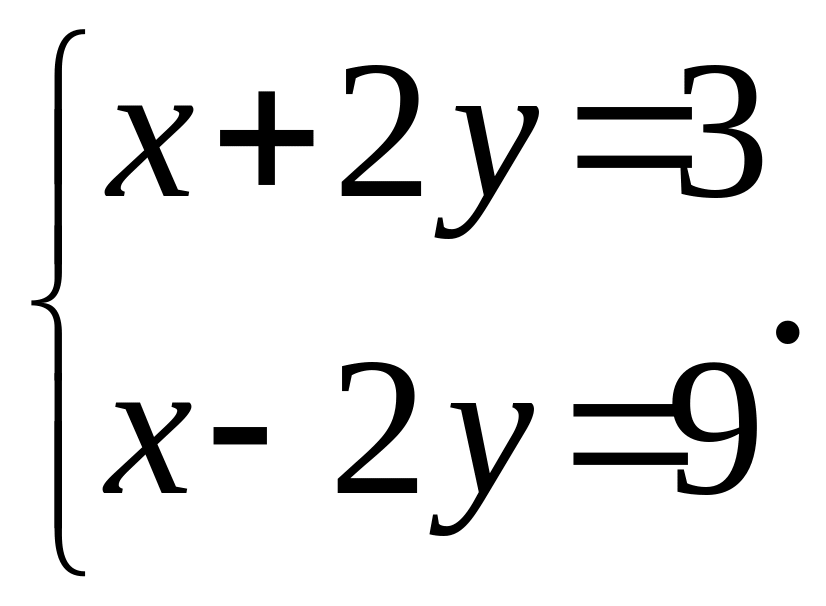
2.1.5. Общие свойства систем уравнений, которые используются при их решении. Любое уравнение системы можно заменить уравнением ему равносильным, которое получают из исходного с помощью элементарных преобразований:
-умножением обеих частей любого из уравнений на одно и тоже произвольное число, отличное от нуля;
- переменой местами двух любых уравнений;
-прибавлением к обеим частям одного из уравнений системы соответствующих частей другого уравнения, предварительно умноженных на любое действительное число.
2.1.6. Геометрический смысл двух линейных уравнений первой степени с двумя неизвестными. В случае действительных коэффициентов каждое из уравнений системы изображает на плоскости некоторую прямую, поэтому решение системы равносильно нахождению координат точек , общих этим прямым. Если прямые пересекаются (одна общая точка), система имеет единственное решение. Если прямые не пересекаются, то система не имеет решения. Если прямые совпадают, то система имеет бесчисленное множество решений.
2.2. Решение системы линейных уравнений по формулам Крамера .
2.2.1. Рассмотрим решение линейной системы уравнений по формулам Крамера (Г. Крамер (1704-1752)- швейцарский математик).
Замечание.
Этот метод
может использоваться только тогда,
когда определитель системы не равен
нулю. Пусть
задана система уравнений:
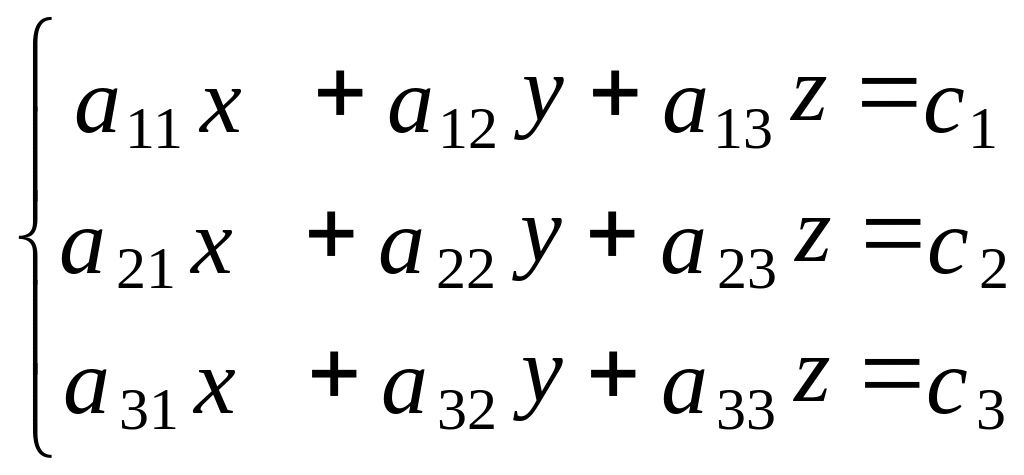 .
.
Последовательность
действий при решении системы уравнений
по формулам Крамера.
1)
Составим и вычислим определитель этой
системы 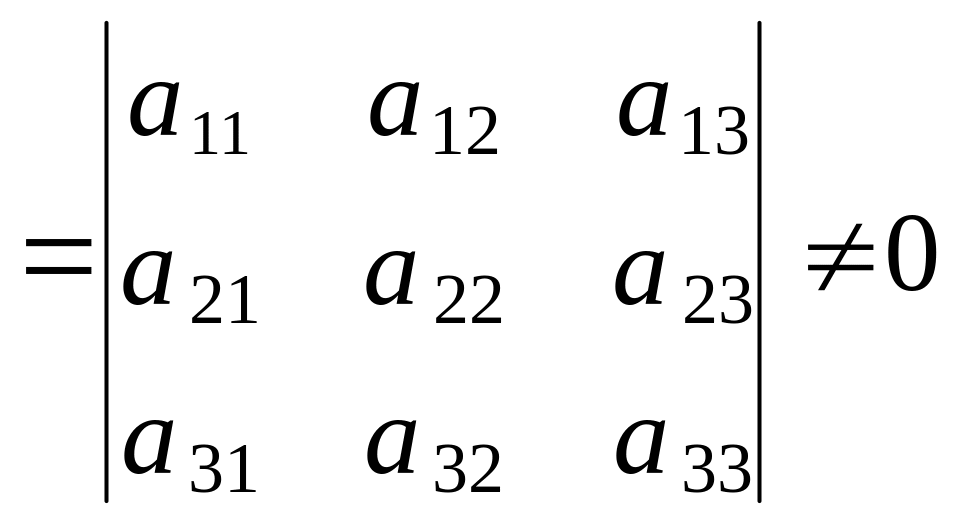 .
.
2) Составим и вычислим определители для неизвестных x , y и z, отличие которых от определителя системы только в том, что в каждом из них столбец коэффициентов неизвестного заменен столбцом свободных членов. В первом определителе заменен первый столбец (коэффициенты при x), во втором столбец коэффициентов при y, в третьем столбец коэффициентов при z.:
x
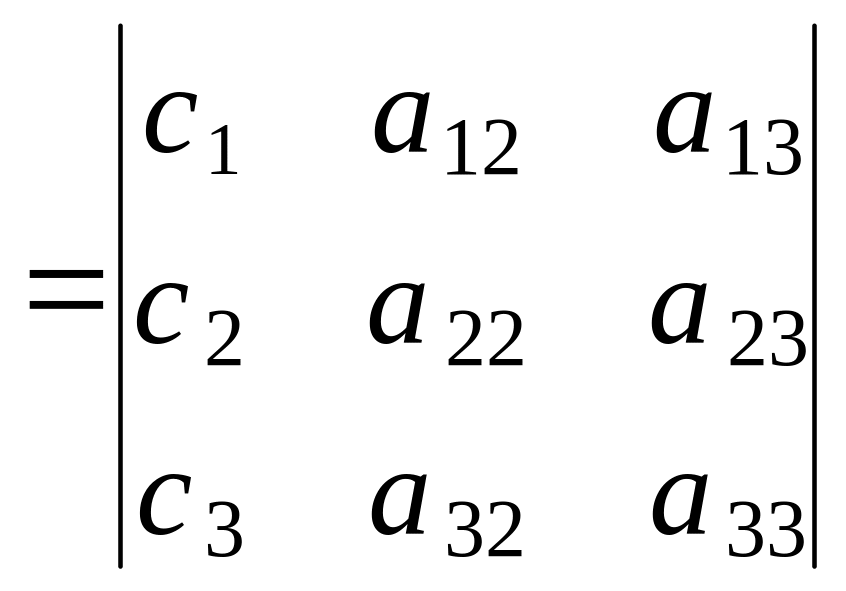 ,
y
,
y ,
z
,
z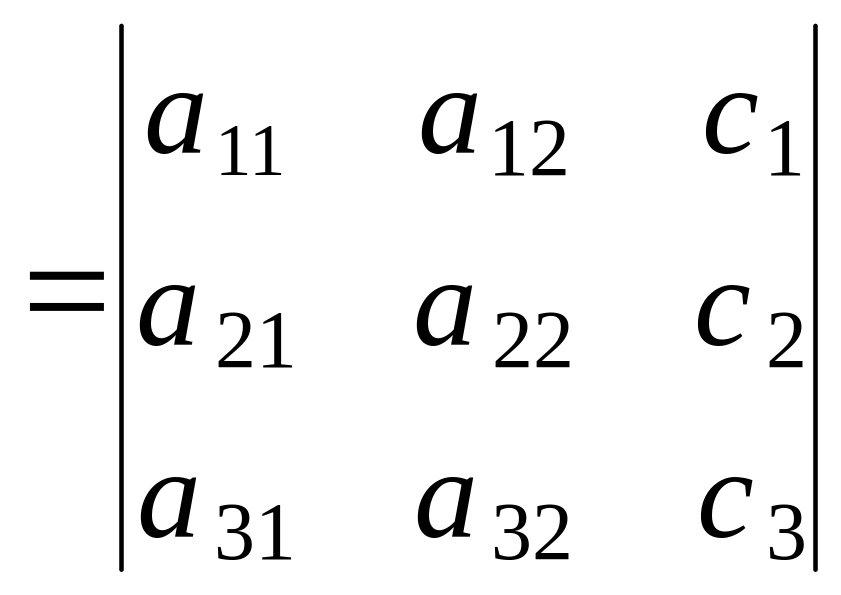 .
.
Находим значения неизвестных по формулам Крамера:
![]() ,
,
![]() ,
,
![]() .
(8)
.
(8)
2.2.2. Пример. Решить систему уравнений по формулам Крамера:
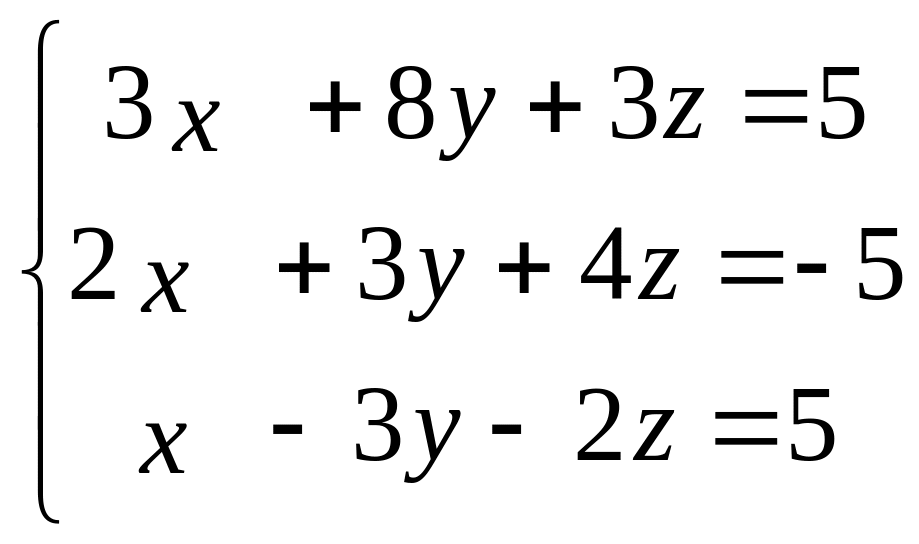 .
.
Решение. 1) составим и вычислим определители системы и при неизвестных:
 x
x
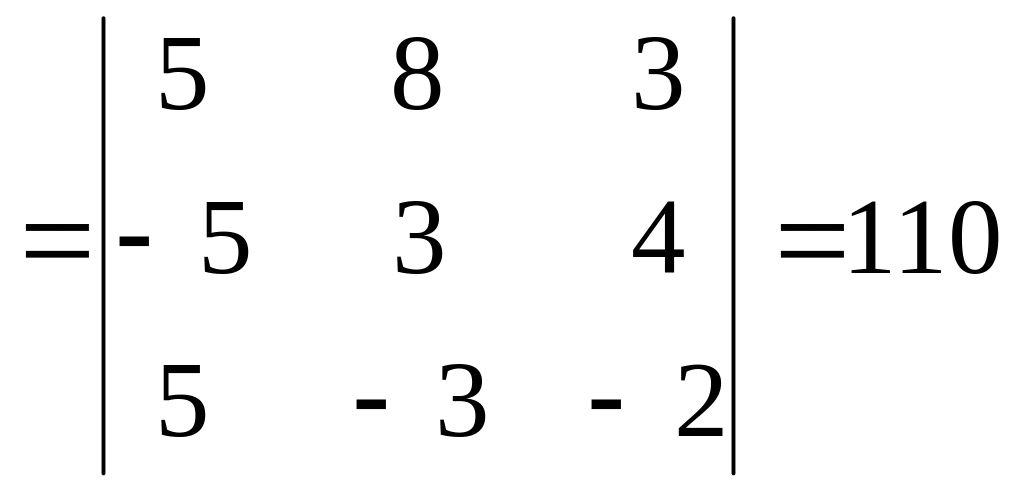
y
 z
z
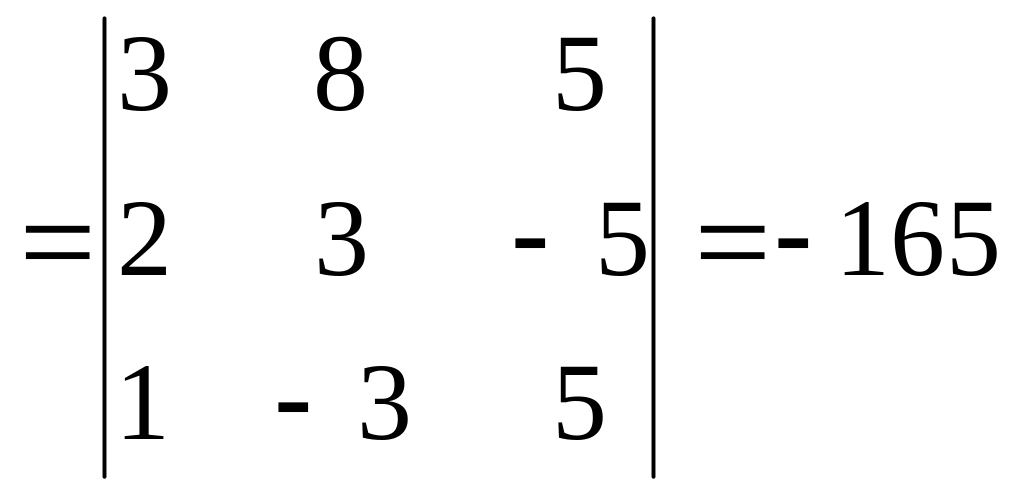
2) По формулам Крамера находим значения неизвестных:
![]() ,
,
![]() ,
,
![]() .
Ответ. (2, 1, -3).
.
Ответ. (2, 1, -3).
