6. Решение однородных систем линейных уравнений.

2.6.1. Однородной системой трех линейных уравнений с 3 неизвестными называется система вида: 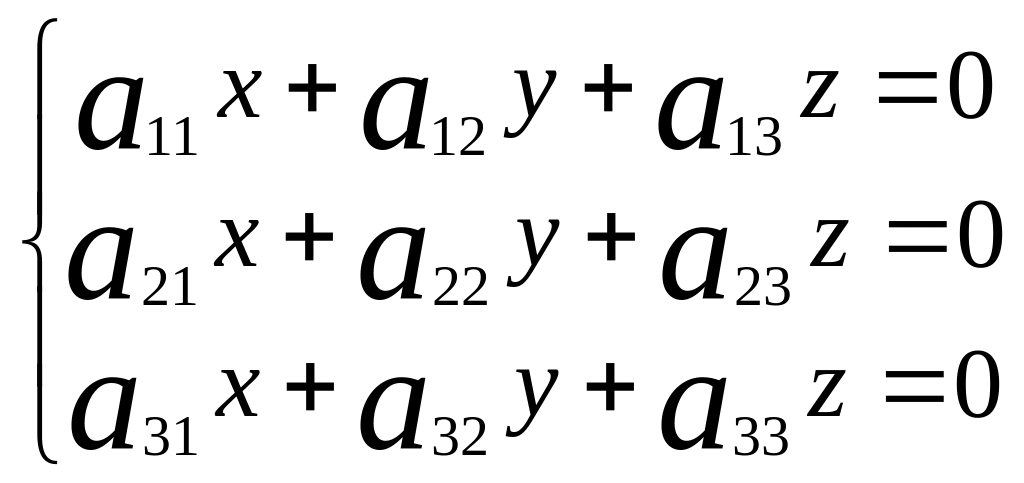(13)

Однородная система всегда совместна, так как очевидно, что x=0, y=0, z=0 образуют решение системы. Здесь могут быть 2 варианта:

1. Если r (A)=n, то нулевое решение будет единственным.

2. Если же r (A)<n, то существует бесчисленное множество решений (ненулевых), что следует из теоремы Кронекера-Капелли. Переменные как и при решении методом Гаусса разделяются на базисные и свободные. Формула, выражающая зависимость базисных переменных от свободных, называется общим решением системы. Свободным переменным можно придавать любое значение, например числа К₁, К₂ и так далее. Значения базисных переменных, полученные при подстановке конкретных значений свободных, называются частными решениями системы.

Лемма 1. Для того, чтобы однородная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю. Лемма 2. Если в однородной системе число уравнений m меньше числа переменных n, то система имеет ненулевое решение. 2.6.2. Пример. Решить систему линейных уравнений . Решение. Составим и исследуем матрицу системы. 1) Вычтем из третьей строки вторую. 2) Переставим первый и третий столбцы. 3) Из второй строки вычтем первую. 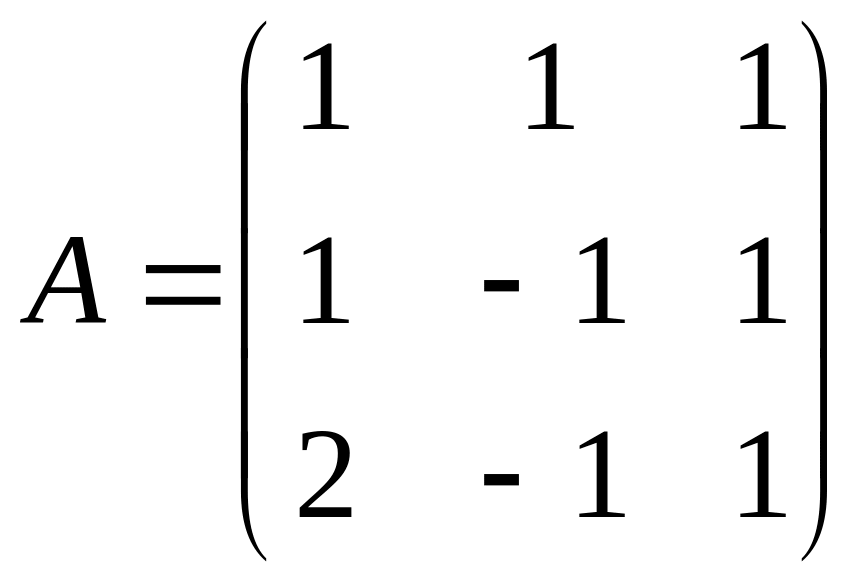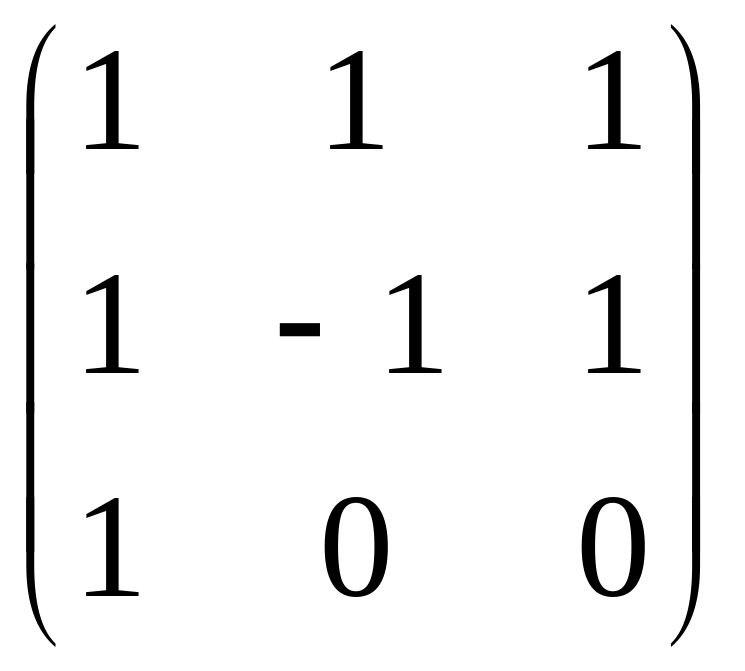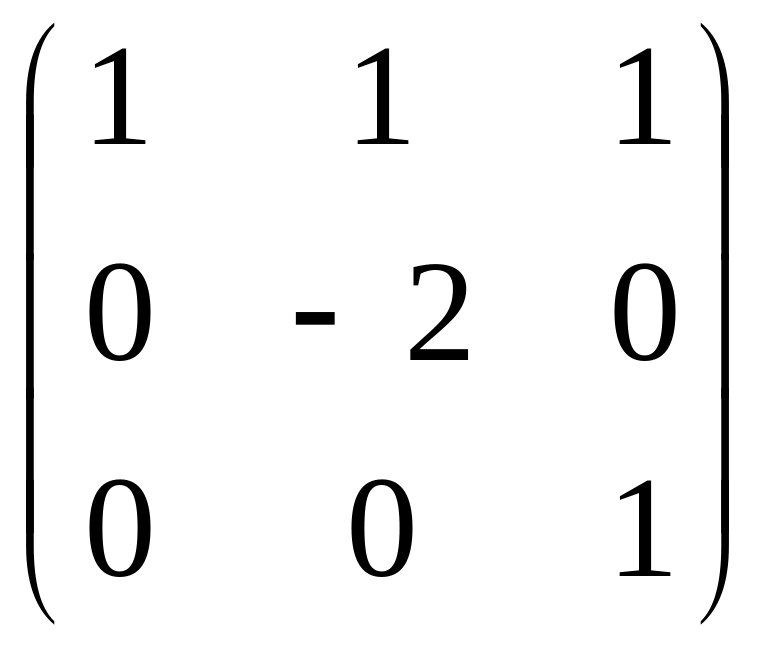   r(A)=3 ( n=3).

Вывод: система определена и имеет единственное решение: x=y=z=0. 2.6.3. Пример. Решить систему линейных уравнений 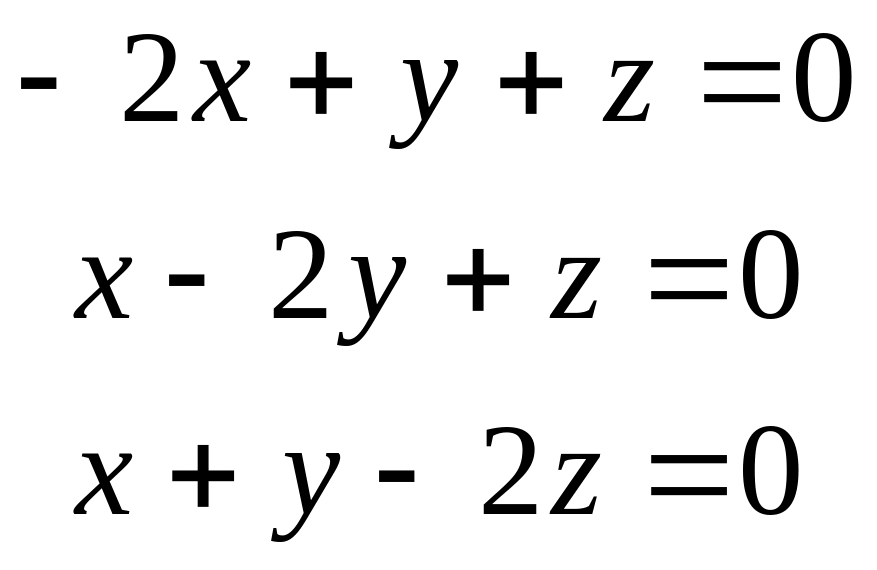. Решение. Составим и исследуем матрицу системы:

1. Прибавим к третьей строке первую.

2. Прибавим к третьей строке вторую.

3. Вторую строку меняем местами с первой.

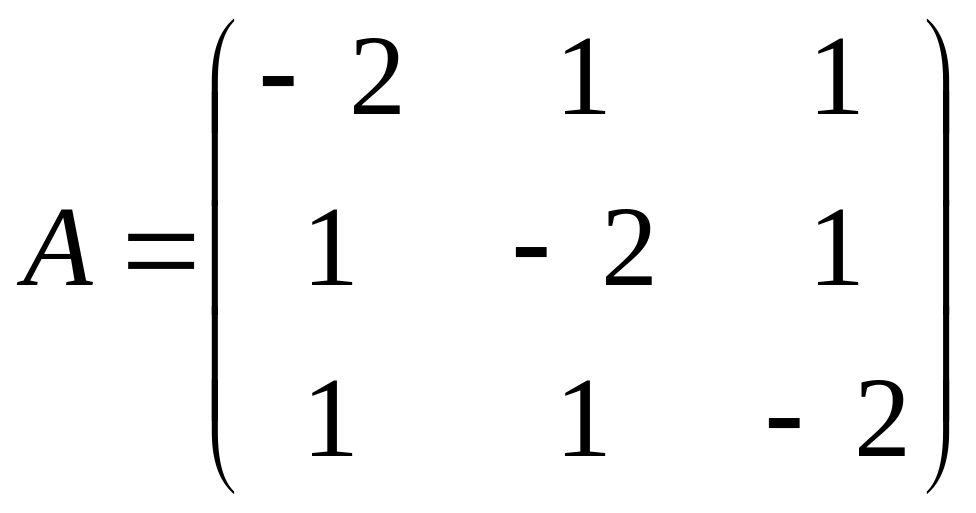
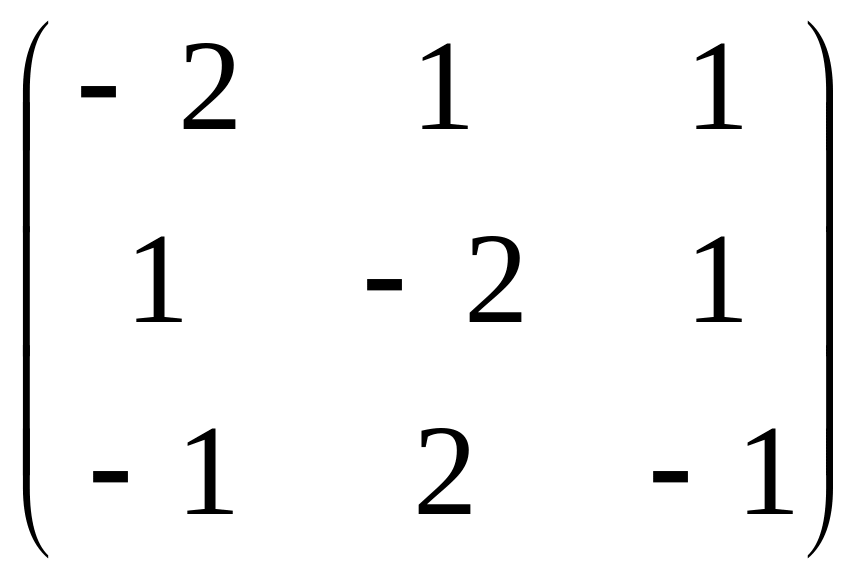
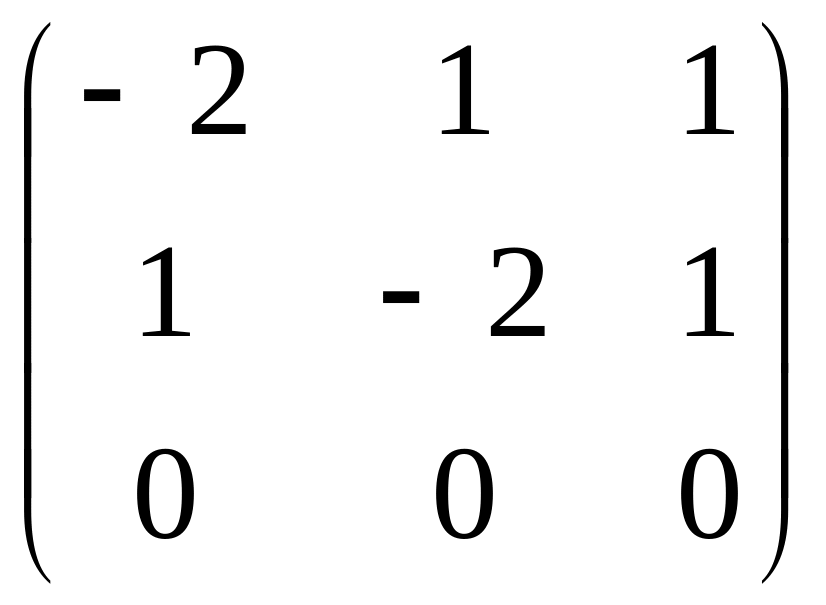
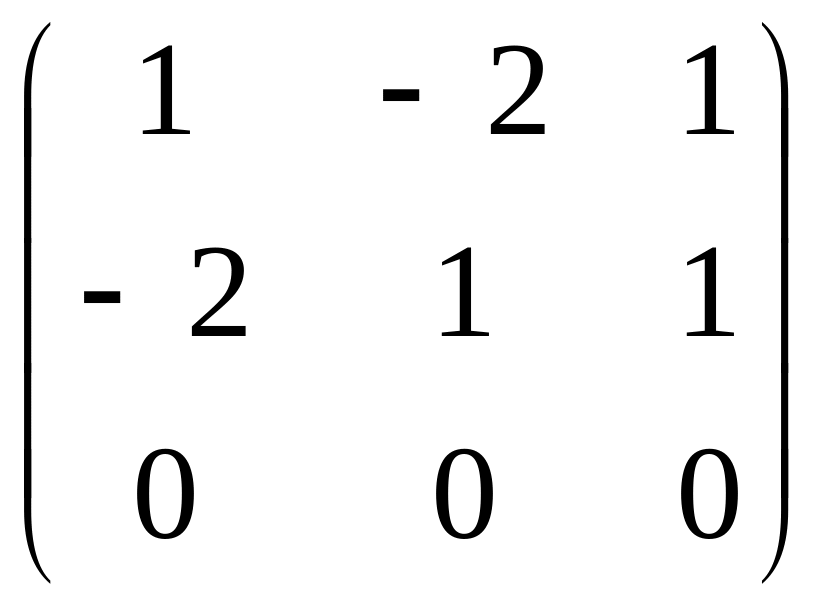
4) Ко второй строке прибавляем удвоенную первую. 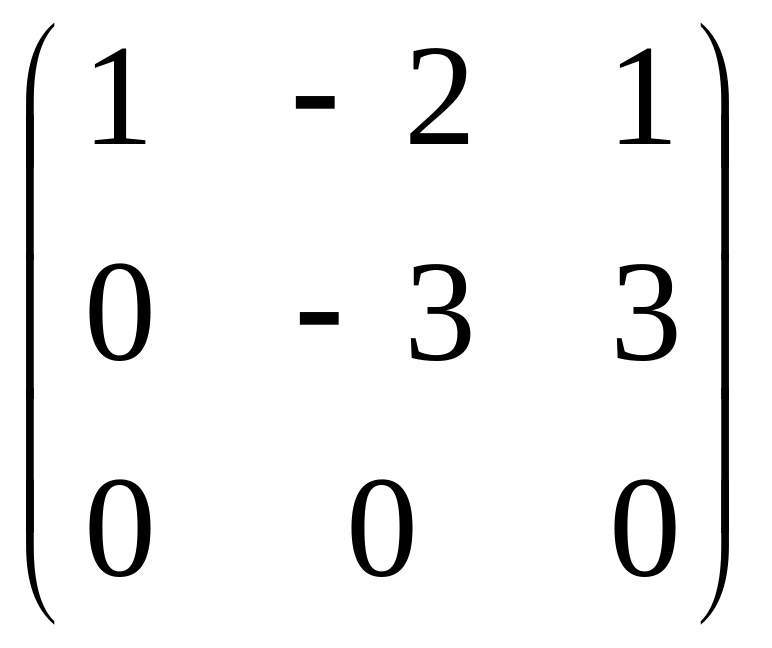     r(A)=2 , (n=3). Полученная матрица эквивалентна системе двух уравнений, из которой находим общее решение системы

.

Следовательно, одну переменную z можно считать свободной и ее значения задавать произвольно, например, z=2, тогда можно найти базисные переменные x и y. Одно из частных решений x=y=z=2.

2.7. Практическое занятие №3. «Решение систем линейных алгебраических уравнений».

2.7.1. Решение по формулам Крамера.

Пример 1. Дано:

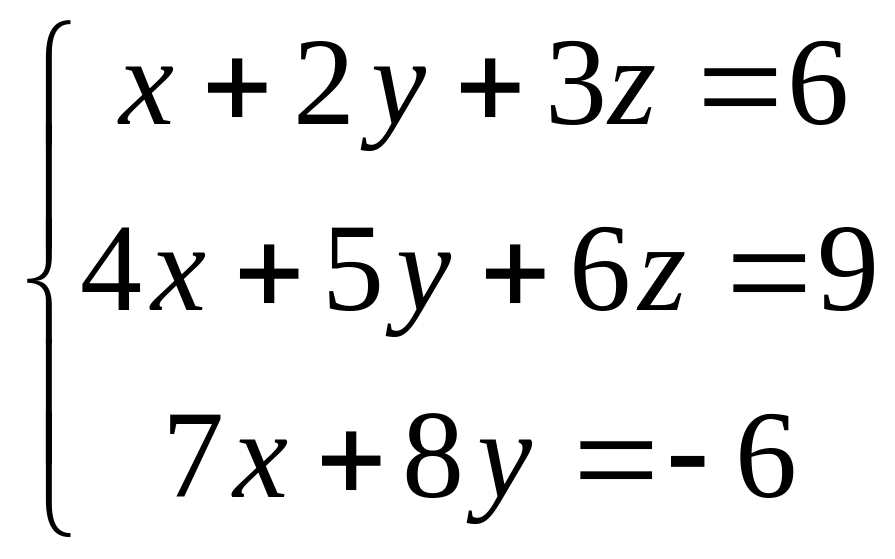. Решить систему уравнений по формулам Крамера.

Решение. Найдем определитель матрицы системы .Так как D  , то решение системы существует и оно единственно. Найдем D₁, D₂ и D₃:

, , .

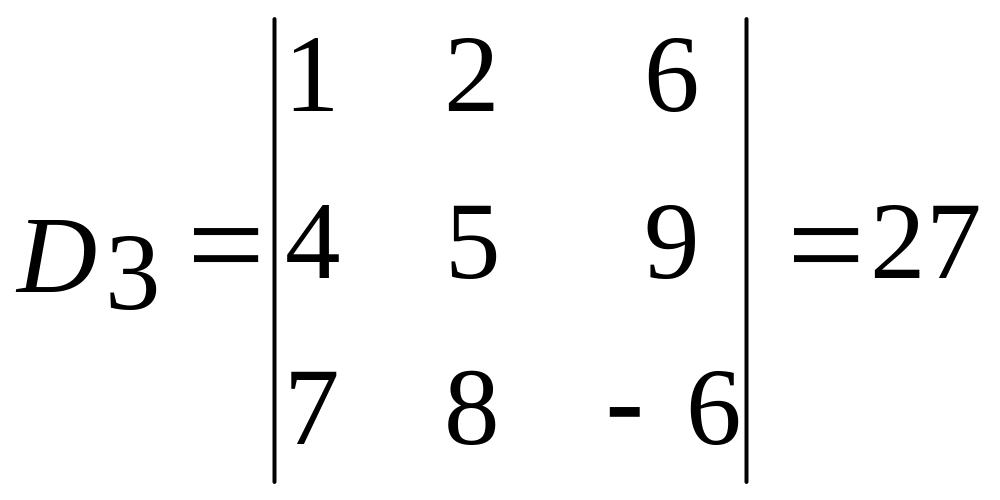Находим решение: Ответ: (-2;1;1).

2.7.2. Примеры для самостоятельного решения систем уравнений

по формулам Крамера:

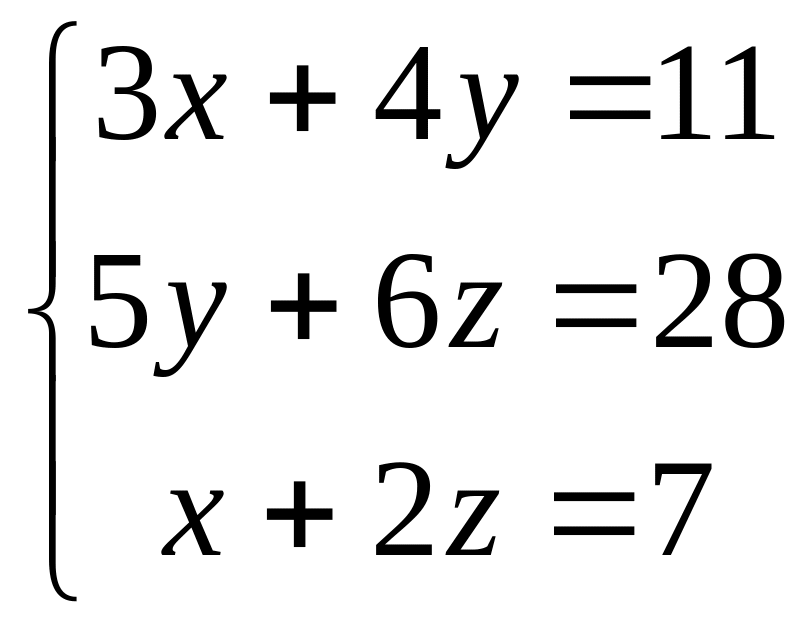1). , 2) 3). , 4). .

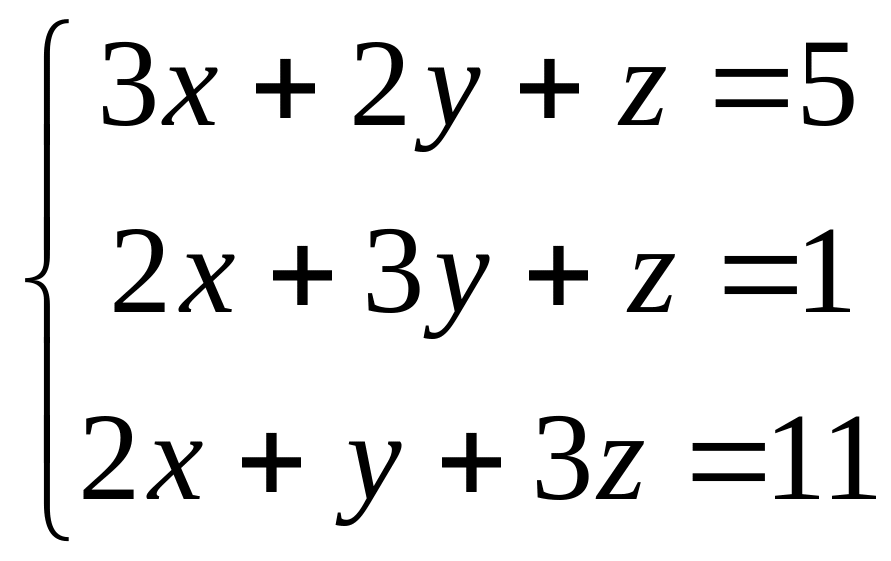Ответы: (-7, 5), (2  3), (1, 2, 3), (2, –2, 3).

2.7.2. Решение систем уравнений матричным способом:

1).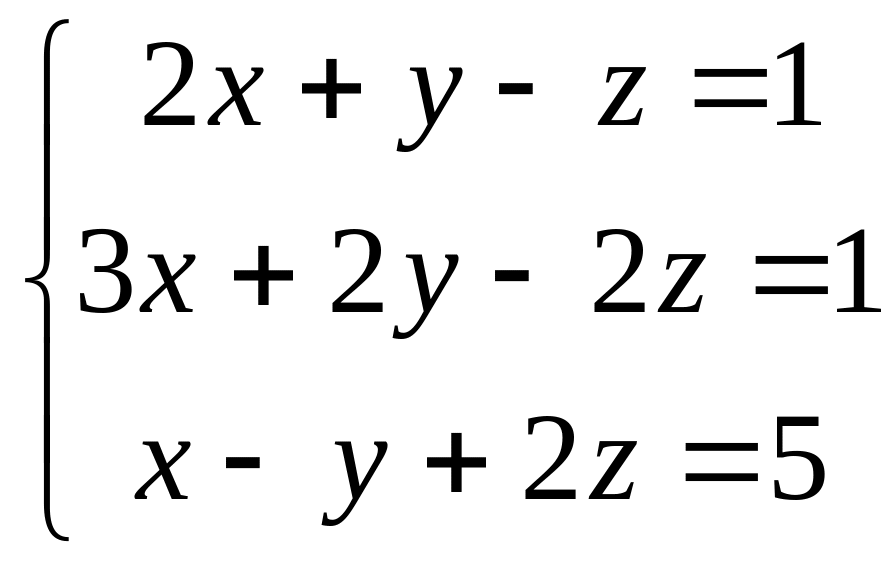 , 2). 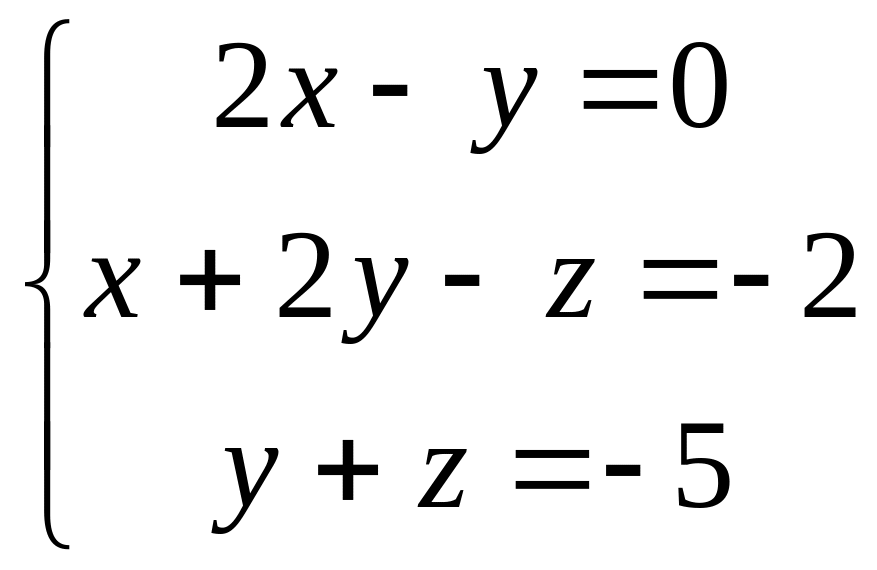. Ответы.(1, 2, 3), (–1,–2,–3).

3. Решение систем уравнений методом Гаусса.

Пример 3. Предприятие выпускает 3 вида продукции, используя сырье 3 видов. Числовые характеристики приведены в таблице:

Таблица. Расход видов сырья на 1 изд.

Вид сырья на 1 изд.	№1	№2	№3	Запас сырья вес.ед.
№1 №2 №3	6 4 5	4 3 2	5 1 3	2400 1450 1550

Обосновать прогноз объема выпуска продукции каждого вида при заданных запасах.

Решение.

Обозначим неизвестные объемы выпуска продукции каждого вида через x, y, z. Составим балансовые соотношения в виде системы 3 уравнений с 3 неизвестными:

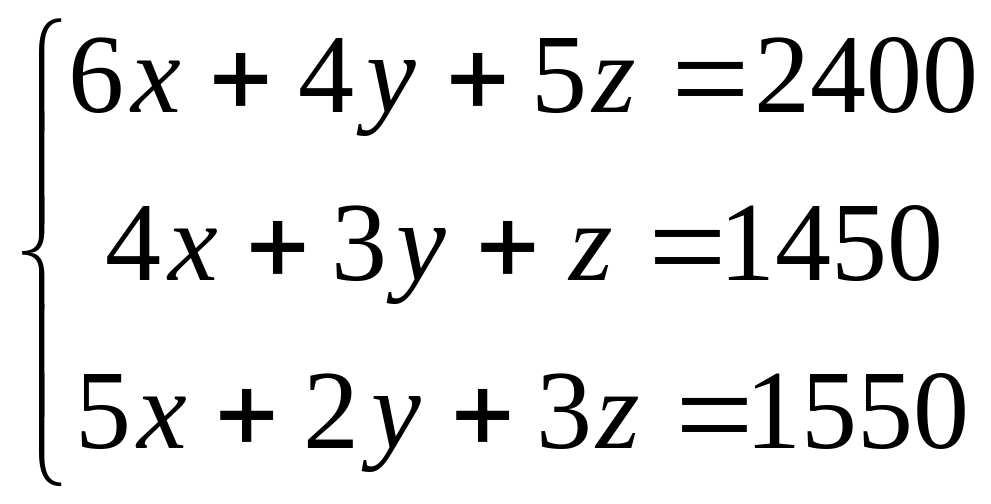. Составим расширенную матрицу системы уравнений:

= = = .

Полученной треугольной матрице эквивалентна система уравнений: , откуда мы находим ответ прогноз выпуска продукции: x=150, y=250, z=100.

2.7.4. Решить самостоятельно: 1). , 2). .

Ответы. 1) (1, 2, 3), 2) (1,–1,3).