3.4.11. Расстояние между двумя точками в пространстве.

Пусть в пространстве заданы координаты точек: А(x₁, y₁, z₁) и С(x₂, y₂, z₂) , требуется найти расстояние между ними. Искомое расстояние равно модулю вектора АС, координаты которого равны разности координат его конца и начала:

.

Теперь находим модуль вектора, то есть расстояние между заданными токами: . (3)

3.4.12. Деление отрезка в заданном отношении.

Пусть в пространстве задан отрезок, известны координаты его начала и конца: А(x₁, y₁, z₁₎ и С(x₂, y₂, z₂)_. Требуется найти координаты точки, лежащей на этом отрезке и делящей его в отношении  . Координаты этой точки определяются формулами:

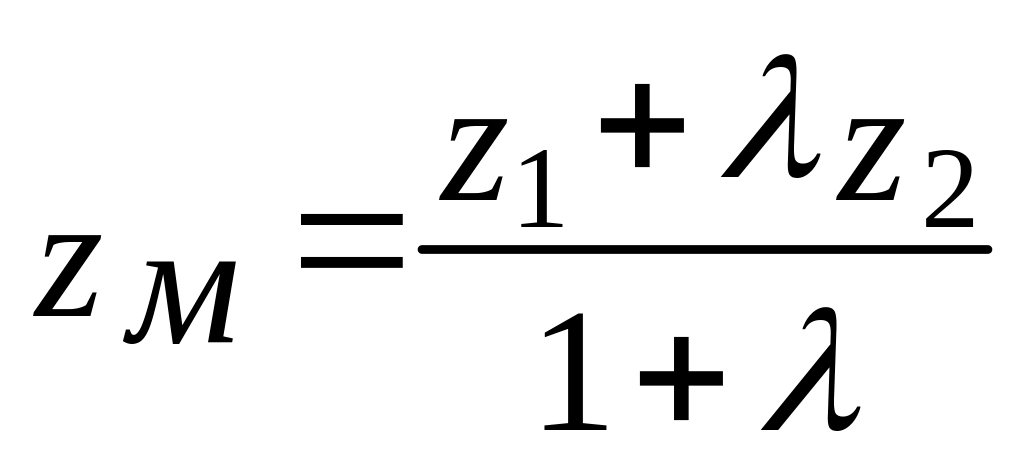, , . (4)

3.4.13. Векторы в экономике. В экономике вектором называется упорядоченный набор чисел, например, Р(1,5,3). Числа в векторе с учетом их расположения по номеру в наборе называются компонентами (составляющими) вектора. Число компонент вектора называется его размерностью. Так, Р(1,5,3)– трехмерный вектор. При этом на них распространяются все рассмотренные выше линейные операции над геометрическими векторами.

3.4.14. Пример. Завод производит электроутюги, электрочайники и электронагреватели. Годовой объем производства в 2002 году характеризуется вектором S₂₀₀₂( 1000, 1500, 800). В 2003 году произвели на 10% больше продукции, тогда S₂₀₀₃( 1100, 1650, 880). Найдем суммарный объем производства за 2 года S₂₀₀₂+ S₂₀₀₃=S(2100, 3150, 1680).

Действия с векторами это распространение действий над числами.

3.5. Скалярное произведение векторов.

3.5.1 Скалярным произведением двух векторов называется число, равное произведению длин (модулей) этих векторов на косинус угла между ними: .

3.5.2. Свойства скалярного произведения:

1. .

2. пр_a пр_b .

3. 

4. 

3.5.3. Необходимое и достаточное условие перпендикулярности двух не нулевых векторов: . Отсюда следует, что: . ; .

3.5.4.Скалярное произведение векторов может быть выражено через их координаты:

Пусть , , тогда

.

То есть, скалярное произведение векторов равно сумме парных произведений одноименных проекций.

3.5.5. Пример. Годовой объем производства в 2002 году характеризуется вектором

S₂₀₀₂( 1000, 1500, 800). Средняя цена за единицу продукции в условных единицах была С₂₀₀₂(15, 20, 50). Найти суммарную стоимость проданной продукции СПР.

Решение. Очевидно, что суммарная стоимость проданной продукции определится скалярным произведением:

СПР= S₂₀₀₂  С₂₀₀₂=100010+150020+80050=80000 у.е. Ответ. 80000 у.е.

6. Для геометрических векторов для определения длины вектора справедлива формула: . В тех случаях, когда компоненты вектора имеют разную размерность или наименование эта формула не применяется, например, на конкурсе красоты рассматривается вектор всем известная тройка чисел: (90,60,90) и всем понятно, что не имеет смысла ни модуль этого вектора, ни сложение его с другими векторами

3.5.7. Из формулы скалярного произведения векторов можно определить косинус угла между векторами:

. (5)

Условие перпендикулярности двух векторов, выраженное через их координаты будет .

3.5.8.Пример. Найти вектор , если он перпендикулярен вектору и он составляет тупой угол с осью Оу.

Решение.. Так как , то . Так как , то . Получим систему и решаем ее:

Так как по условию составляет тупой угол с осью Оу, то получим ответ .

3.5.9. Пример. Могут ли являться вершинами невырожденного треугольника координаты трех точек в пространстве: ?

Решение. Треугольник является невырожденным, если неколлинеарен .

Найдем координаты этих векторов:

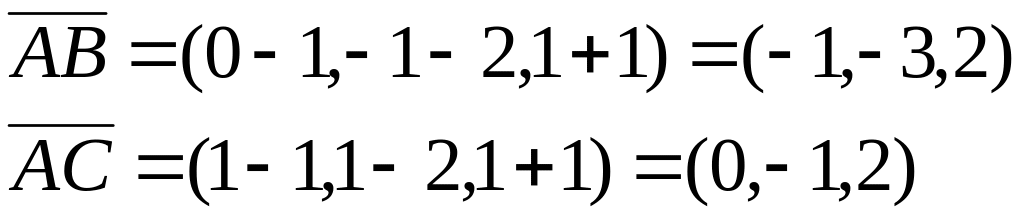
Условие коллинеарности не выполняется, так как .

Ответ: является невырожденным.