1.2.2. Свойства операций сложения (вычитания) матриц:

1. А+В=В+А 2. А+(В+С)=(А+В)+С 3. А+О=О+А=А, где О – нулевая матрица.

1.2.3. Умножение матрицы на число.

Произведением числа λ на матрицу А или матрицы А на число λ называется матрица, все элементы которой получены из исходной матрицы А умножением их на число λ. Пример: умножим матрицу на число λ=5: .

1.2.4. Свойства операции умножения матриц на число: 1. 1·А=А·1=А, 2. 0·А=А·0=0, 3. λ·(α·А)=(λ·α)А= λ·α·А, 4. (λ+α)·А= λ·А+α·А, где λ, α – числа.

Замечание. Разность двух матриц А и В одинаковых размерностей определяется формулой А–В=А+(–1) В.

1.2.5. Пример. Завод в октябре месяце поставил обувь в 2 города. Поставки можно охарактеризовать матрицами в первый город А1, во второй –А2:

,

в первых столбцах этих матриц количество коробок с мужской обувью, во вторых – женской, в третьих – детской. В первых строках матриц количество коробок с обувью черного цвета, во вторых – коричневого, в третьих – белого. На следующий месяц поступил заказ с увеличением поставки в первый город на 50%, а во второй на 25%. Найти матрицы, характеризующие суммарные поставки обуви в 2 города по месяцам.

Решение. Общая поставка обуви в 2 города в октябре определяется суммой: .

Поставка в ноябре в эти 2 города определяется как линейная комбинация матриц:

.

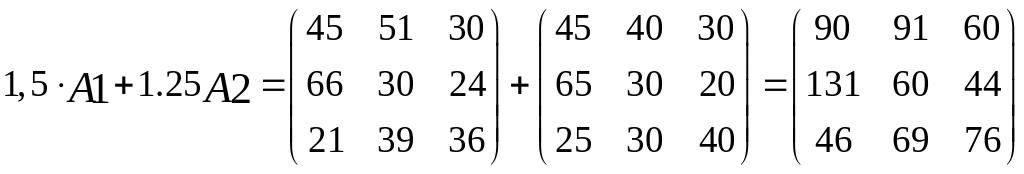1.3. Умножение матриц.

1.3.1. Произведением матрицы А_mn порядка m на n на матрицу В_np порядка n на p называется матрица С_mp порядка m на p, все элементы которой с_ij равны сумме парных произведений элементов i-той строки матрицы А на элементы j-того столбца матрицы В. (3)

Замечание. Из определения следует, что перемножать можно только такие матрицы А и В, у которых число столбцов матрицы А равно числу строк матрицы В. Целой положительной степенью А^m квадратной матрицы А называется произведение m матриц А. 1.3.2. Пример. Умножить матрицу 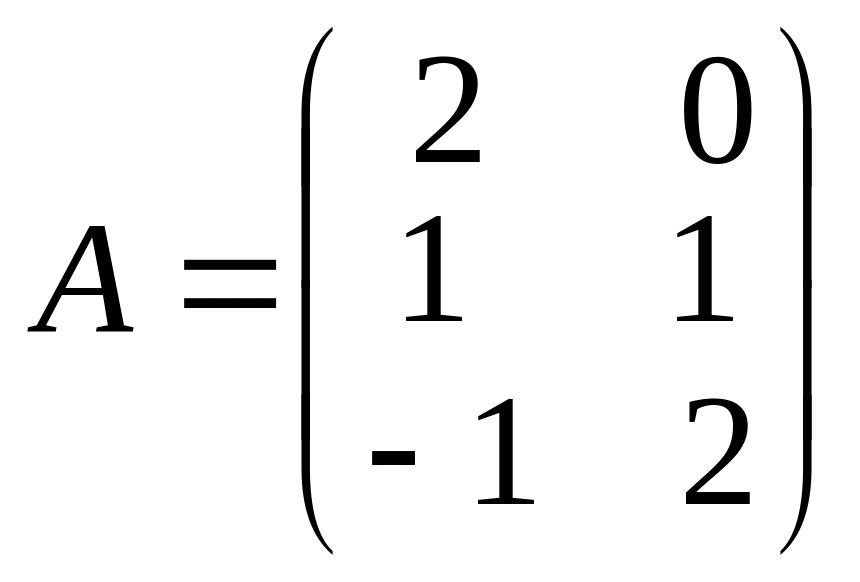на матрицу . Решение.

. .

1.3.3. Пример.

Для ежемесячного подсчета выручки, для контроля за поставками и производством удобнее вести расчеты в матричной форме. Данные таблицы по объему продаж разных видов продукции по различным каналам сбыта представим в виде матрицы А, а цену разных видов продукции в виде матрицы–столбца Х. Вычислим произведение матриц АХ: ; .

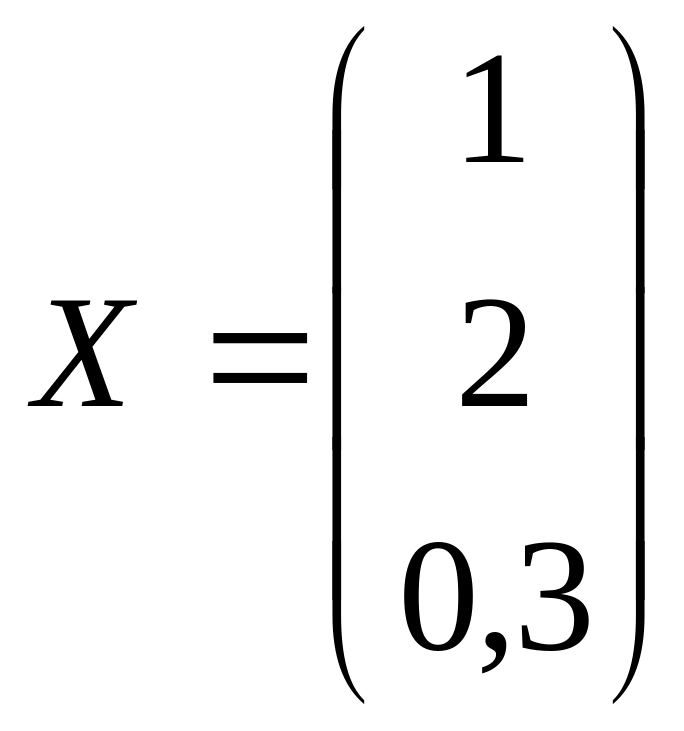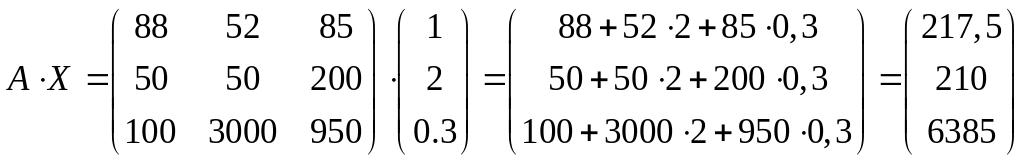. Мы получили матрицу, элементы которой несут информацию о выручке с продаж за месяц по каждому направлению сбыта.

1.3.4. Пример. Дано , . Вычислить 2А–3В, С=А²+В.

1.3.5. Свойства операции умножения матриц (предполагается, что соответствующие матрицы можно перемножать):

1. А · Е = Е · А = А, 2. А · (В · С) = (А · В) · С,

3. (А+В) · С= А · С + В · С. 4. ==.

5. В общем случае А·В≠В·А, однако есть матрицы, для которых А·В=В·А, такие матрицы называются перестановочными. Например, перестановочны любая квадратная матрица с единичной матрицей того же порядка, что отмечено в первом свойстве. Кроме того, перестановочныe диагональные матрицы одного порядка

6. Произведение двух ненулевых матриц может быть нулевой матрицей. Пример: вычислим произведение матриц . При перемножении матриц получаем . 1.3.6. Операция транспонирования матрицы заключается в замене строк матрицы ее столбцами, столбцов строками с сохранением порядка следования ; A^T= . Если А симметричная матрица, то А^т=А. 1.3.7. Свойства операции транспонирования: (А^т)^т=А; (kА)^т=kA^т ; (А+В)^т=А^т +В^т; (АВ)^т=В^тА^т.

1.4. Определители квадратных матриц 1.4.1. Для квадратной матрицы А вводится числовая характеристика, называемая определителем. Число строк матрицы определяет порядок определителя. Определитель матрицы второго порядка А₂= вычисляется по формуле: det(А₂) = . (4)

Определитель равен разности произведений элементов, стоящих на главной и побочной диагоналях, он обозначается либо detA, либо . Значения индексов при элементах определителя имеют тот же смысл, что и в матрицах.

1.4.2. Пример. Вычислить определители второго порядка: А) . В)

1.4.3. Определитель матрицы 3-его порядка определяется по формуле (первый способ ) det(A₃) = =a₁₁a₂₂a₃₃+a₂₁a₃₂a₁₃+a₁₂a₂₃a₃₁ -

–a₃₁a₂₂a₁₃–a₂₁a₁₂a₃₃–a₃₂a₂₃a_11. (5)

1.4.4. Схема составления произведений по правилу треугольников (второй способ):

=

Рассмотрим диагональную схему вычисления определителя третьего порядка с дописыванием столбцов. К определителю справа приписываются два первых столбца, образуются три диагонали параллельные главной («падающие») и три параллельные побочной («растущие»). Произведения элементов определителя, стоящих на «падающих» диагоналях берутся со знаком плюс, а на «растущих» со знаком минус.

= a₁₁a₂₂a₃₃+a₂₁a₃₂a₁₃+a₁₂a₂₃a₃₁–

–a₃₁a₂₂a₁₃–a₂₁a₁₂a₃₃–a₃₂a₂₃a_11.

1.4.5. Пример. Вычислить определитель .

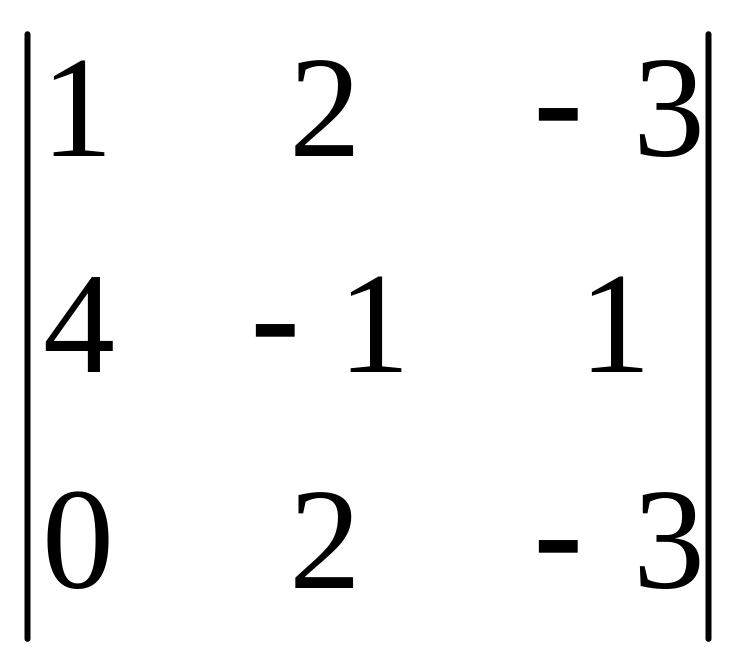Решение. Воспользуемся вторым способом вычисления определителя: =1 · (–1)·(–3) + 2·1·0 + (–3)42 –0·(–1)·(–3) – 2·1·1 – (–3)42 =1. 1.4.6. Минором M_ij элемента a_ij квадратной матрицы A_n называется определитель, полученный вычеркиванием i- строки и j- столбца.

1.4.7. Алгебраическим дополнением элемента a_ij матрицы A_n называется соответствующий минор M_ij , взятый со знаком плюс, если i+j=2k; и знаком минус, если i+j=2k+1. A_ij=(-1)^i+jM_ij (6)

1.4.8. Пример. Для матрицы вычислить минор М₁₂ и алгебраическое дополнение А₁₂.

Решение. M₁₂= , А₁₂=(–1)¹⁺² М₁₂= –6. Ответ. М₁₂=6, А₁₂=–6.

Задание: вычислить самостоятельно А₃₂ и А₃₃.

1.4.9. Теорема разложения определителя. Определитель n-ого порядка вычисляется как сумма произведений элементов какой-либо его строки (столбца) на их алгебраические дополнения. Приведем разложение определителя третьего порядка по элементам i-строки, а затем j-cтолбца.

a_i1 · A_i1 + a_i2 · A_i2 + a_i3 · A_i3. i=1,2,3;

a_1j · A_1j + a_2j · A_2j + a_3j · A_3j. j=1,2,3.