2.5. Решение систем линейных уравнений методом Гаусса.

2.5.1. Основные определения. Пусть надо решить систему из трех уравнений с тремя неизвестными: .

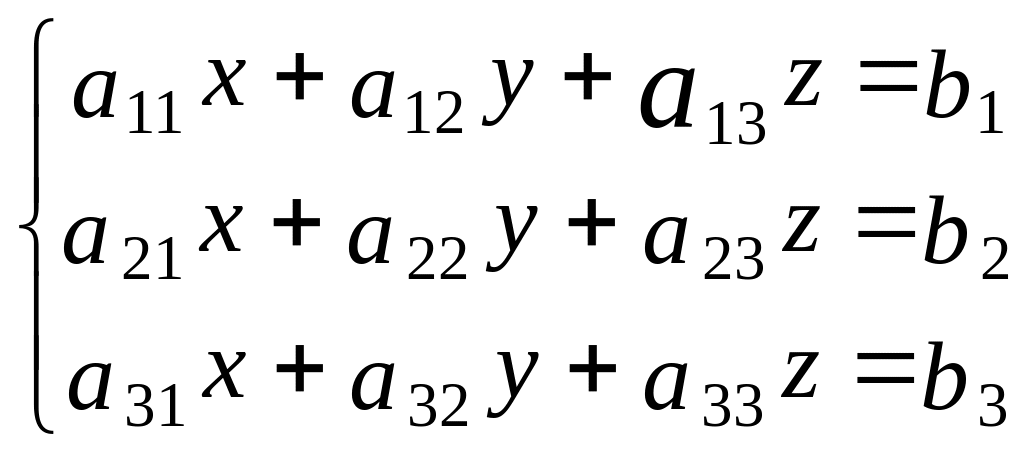Составим расширенную матрицу системы, в которой содержится вся информация о системе: .

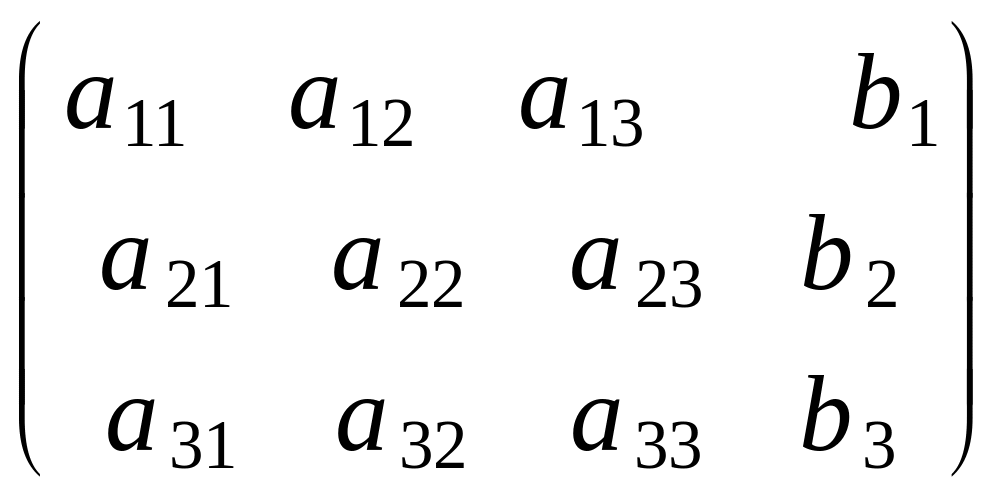Известно, что при элементарных преобразованиях системы уравнений множество ее решений не меняется, об этом говорилось п.2.1.6. Элементарные преобразования расширенной матрицы эквивалентны элементарным преобразованиям системы линейных уравнений.

2.5.2. Элементарные преобразования с расширенной матрицей системы включают в себя:

• перемена местами строк (столбцов),

• умножение или деление строки (столбца) на число, отличное от нуля,

• прибавление к элементам строки (столбца) соответствующих элементов другой,

• вычеркивание одной из двух одинаковых строк или нулевой строки.

После того, как матрица приведена к виду, позволяющему найти решение или решения, возвращаются к эквивалентной системе уравнений.

Рассмотрим возможные варианты: 1. Под или над главной диагональю матрицы все элементы равны нулю:

А = , здесь буквами обозначены цифры. В этом случае система определена и имеет единственное решение, неизвестные вычисляются из эквивалентной треугольной системы:

.

Из третьего уравнения находим z, затем из второго y, а из первого x. 2. Если при преобразованиях расширенной матрицы одно уравнение отбрасывается и остается трапециевидная матрица 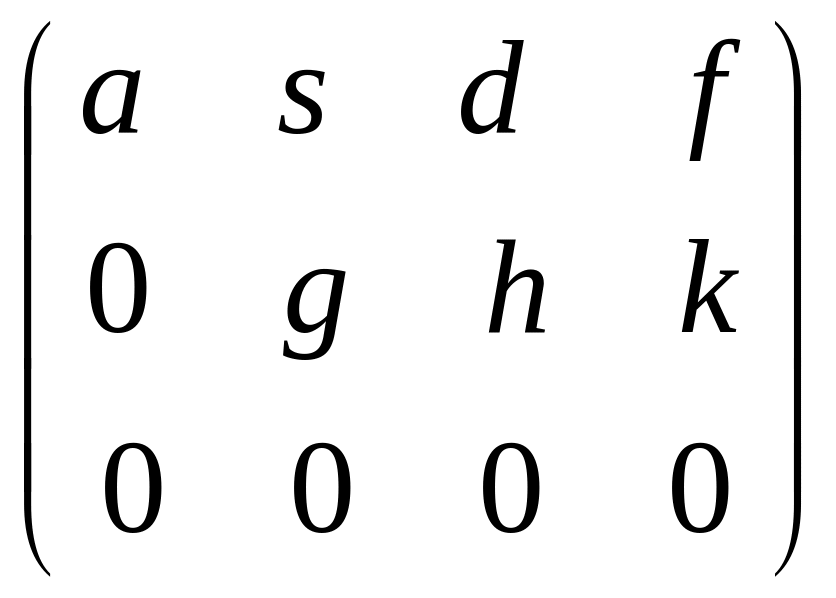, то ее эквивалентная система имеет бесчисленное множество решений .

Общим решением этой системы будет .

Здесь z–свободное неизвестное, ему можно придавать любое значение, а x и y базисные неизвестные, которые вычисляются из общего решения.

3. При преобразовании матрицы получена строка вида (0 0 0 7). В этом случае система несовместна, так как эта строка не может быть заменена равносильным уравнением.

2.5.3. Последовательность элементарных преобразований расширенной матрицы системы.

Первый шаг, надо получить в левом верхнем углу матрицы число 1. Этого можно добиться с помощью перестановки строк или делением первой строки на элемент a₁₁.

Второй шаг, вычитание из второй, а затем и третьей первой строки, умноженной на число равное первому элементу строки, из которой производится вычитание. В результате в первом столбце матрицы второй и третьей строк получаются нули. Эта процедура (первый и второй шаги) повторяется для элемента a₂₂. В итоге будет получена матрица вида (2).

2.5.4. Пример. Решить методом Гаусса систему уравнений .

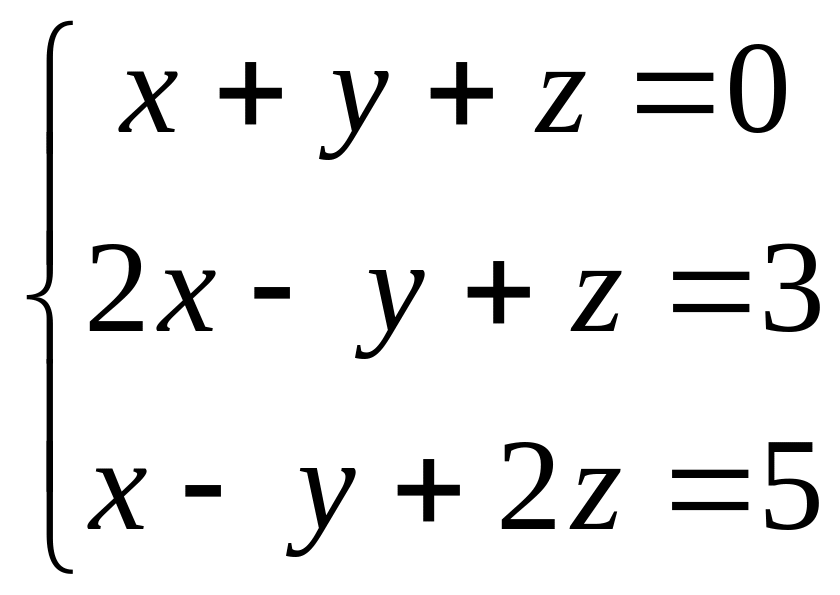Решение. Составим расширенную матрицу системы .

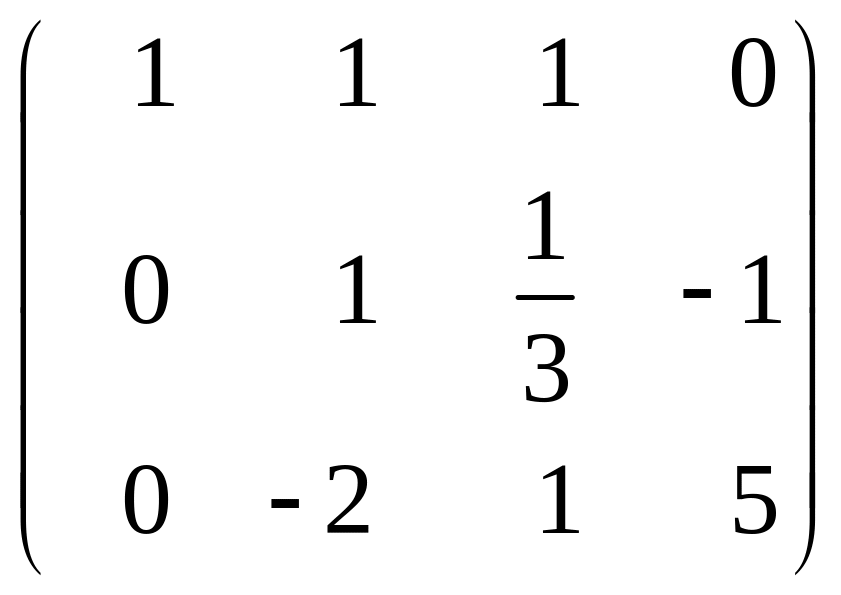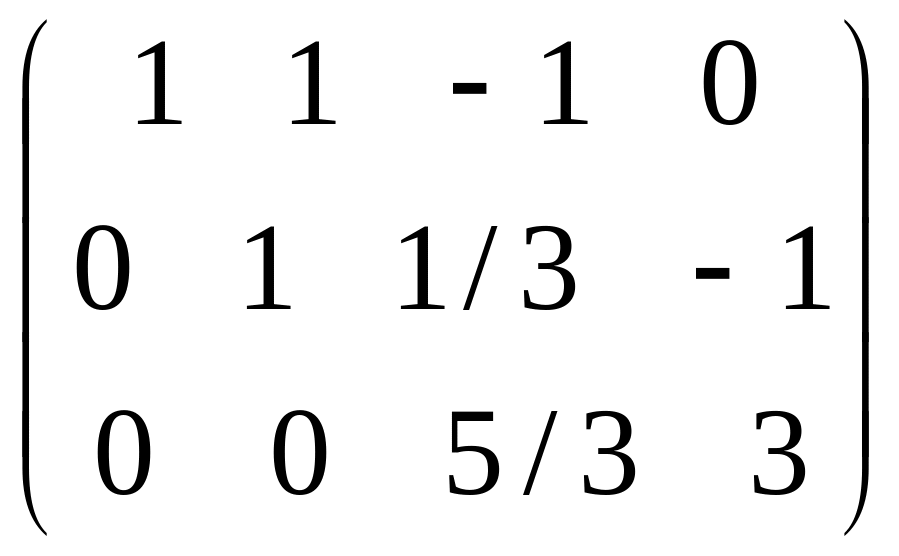
В первой строке в правом углу стоит 1, поэтому переходим сразу ко второму шагу. Из второй строки вычитаем первую, умноженную на 2, а из третьей вычитаем первую. В результате имеем матрицу А₁. Далее делим вторую строку на число –3, получаем матрицу А₂. К третьей строке прибавляем удвоенную вторую – матрица А₃. Записываем эквивалентную систему уравнений А₁= А₂= А₃= 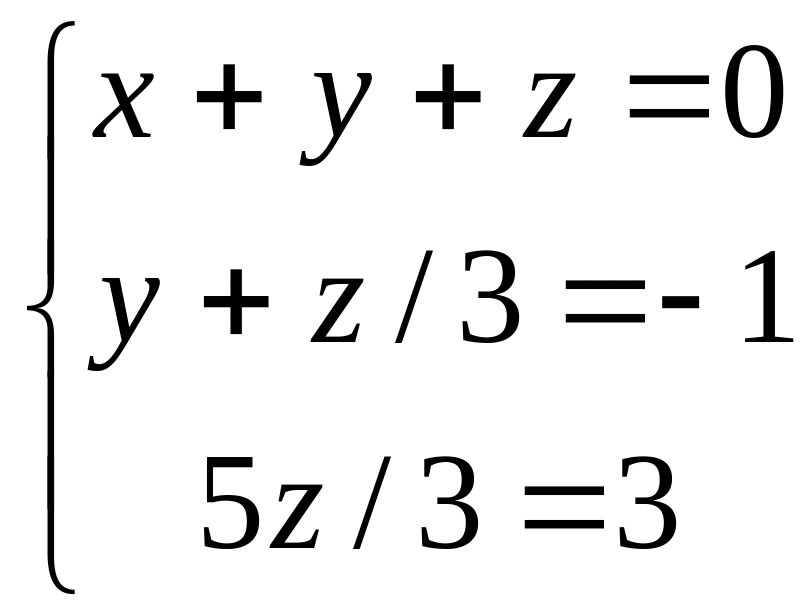 . Из полученной системы уравнений находим единственное решение: .

2.5.5. Пример. Компания должна купить и установить в производственном помещении 2 типа станков. Обозначим количество станков каждого типа через X и Y. Каждая машина первого типа стоит $3000, а второго–$2500, кроме того известно, что X занимает 2 кв. м. производственной площади, а Y– 1 кв.м. Сколько изделий каждого типа компания может купить и установить, если у нее на этот проект выделено $400000 и свободного места, пригодного для установки нового оборудования 240 кв.м.

Решение. Составим систему уравнений: первое–уравнение денежного баланса, второе– условие возможности размещения закупаемого оборудования. Имеем: . Решаем систему уравнений методом Гаусса, составляем расширенную матрицу системы и проводим с ней элементарные преобразования: меняем местами первый и второй столбцы, в верхнем углу получим единицу, затем вторую строку ставим на место первой и делим вторую строку на 1000, а из второй вычитаем первую, умноженную на 2,5. x y y x y x А=    y x  . Эта матрица эквивалентна треугольной системе уравнений

, отсюда легко находим ответ: x=100, y=40.

Вывод: если компания закупит 100 машин первого типа и 40 второго, то будут полностью выполнены требования поставленные в условии задачи.