3.2. Линейные операции над векторами.

3.2.1. Для геометрических векторов введены линейные операции: сложения (вычитания) и умножения вектора на число.

3.2.2. Рассмотрим сумму векторов C+В. Совместим начало вектора В с концом вектора C. Суммой двух векторов C и В называется третий вектор А, начало которого совпадает с началом первого, а конец с концом второго. Координаты вектора А представляют сумму координат слагаемых векторов.

С В

А

Рис.3. Сумма векторов С+В=А.

3.2.3. Разностью векторов А и В называется третий вектор С, координаты которого представляют разность координат первых двух. Вектор С в этом случае начинается в начале первого вектора А (уменьшаемого) и заканчивается в начале второго вектора В (вычитаемого). 3.2.4. Свойства операций сложения (вычитания) векторов: *А+В=В+А. *А+В+С=(А+В)+С=А+(В+С). *А+0=А.

В

С A

Рис.4. Разность векторов А–В=С.

3.2.5. Произведением вектора на число К не равное нулю называют сонаправленный вектор, если К, или противоположный при К , то есть длина вектора умножается на это число.

0,5А А

–0,5А

Рис.5. Умножение вектора А на число.

3.2.6. Свойства операции умножения вектора на число: 1. (А+В)=А+В. 2.()А=А. 3.()==. 3.2.7. Выводы: *Линейные операции над векторами подчиняются правилам действий с алгебраическими выражениями. Векторные равенства можно умножать и делить на любое число, отличное от нуля, переносить векторные величины из одной части равенства в другую с противоположным знаком.

*Множество векторов с действительными составляющими, в котором определены операции сложения векторов и умножения вектора на число, и обладающие свойствами 3.2.4.–3.2.6., называется векторным пространством.

3.3. Действия над векторами в координатной форме

3.3.1. Пусть и , тогда линейные операции над векторами можно выразить как операции над их проекциями.

Пример: Дано: , . Найти сумму и разность этих векторов. . .

3.3.2. Направляющие косинусы вектора. Положение всякого вектора в пространстве определяется углами , которые он образует с координатными осями, косинусы этих углов называют направляющими косинусами данного вектора. Они определяются по формулам:

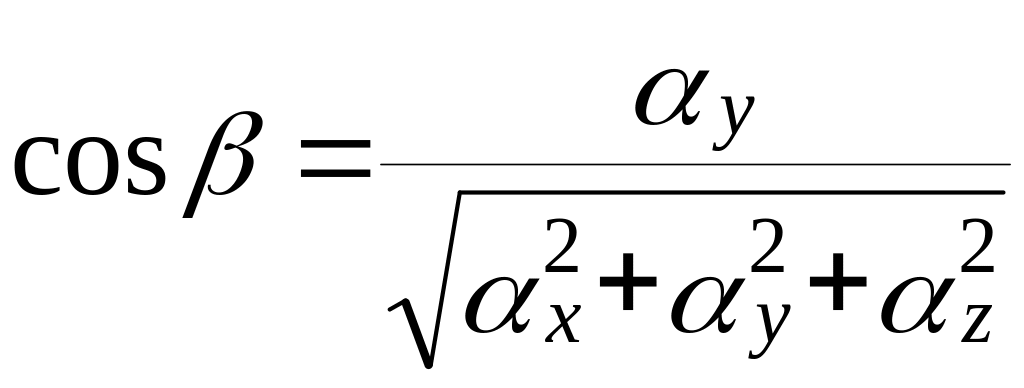, , . (1)

Возводя в квадрат левую и правую части каждого из трех равенств и суммируя их, получаем . Замечание. Векторы, лежащие в плоскости ОXY, описываются двумя координатами, а в пространстве тремя.

3.3.3. Длина вектора (его модуль) определяется формулой:

. (2)

3.3.4. Пример. Дано: А=2В-3С, В=2a–4b, C=4a+3c. Найти вектор А.

Решение. А=2(2a–4b)–3(4a+3c)=4a –8b–12a–9c=–8a –8b –9 c .

Ответ. А= –8a –8b –9 c . Самостоятельно найти А+В+С=