13. Теорема о скоростях точек тела при его плоском движении и следствия о проекциях скоростей двух его точек на ось, проходящую через 2 эти точки.

Скорость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса. 

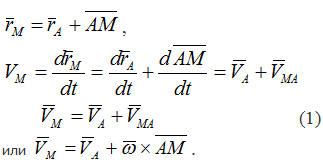
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости  точки  М     при    вращении   ее вокруг точки А.

Вектор V_MA= ω⋅AM перпендикулярен отрезку АМ.

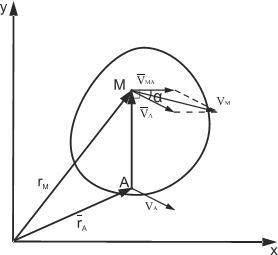
Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов

или спроецировать векторное равенство (1) на выбранные оси координат   

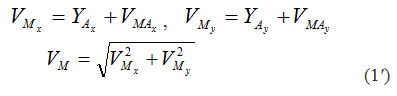
Из теоремы о скоростях точек плоской фигуры следует, что проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны. Это легко показывается в рассуждениях:

так как V_BA⊥AB , то и проекция V_BA  на ось АХ равна нулю.

Следовательно, V_Bx=V_Ax .

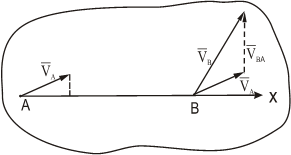
14. Мгновенный центр скоростей. Способы нахождения.

При плоско-параллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей.

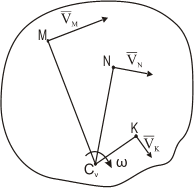
При определении положения МЦС скорость любой точки может быть записана: V_M=V_CV+V_MCV , где точка С_V  выбрана за полюс. Поскольку это МЦС и V_CV=0 , то скорость любой точки определяется как скорость вращении вокруг мгновенного центра скоростей.

       

       

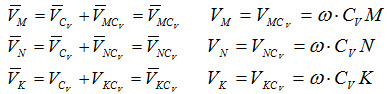
Из рис. видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение 

                                                                    

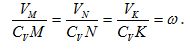
15. Теорема об ускорениях точек тела при плоском движении и следствия о проекциях ускорений двух его точек на ось, проходящую через 2 эти точки.

Ускорение любой точки тела в плоском движении равно геометрической сумме ускорения точки тела в поступательном движении совместно с полюсом и ускорения вращения точки вокруг полюса во вращательном движении тела вокруг полюса.

Дифференцируя по времени выражение , получаем

В последнем выражении вектор углового ускорения тела ε направлен по оси вращения тела, совпадающей с осями Az* и Az₁ , так как при плоском движении вектор ω не изменяет своего направления в пространстве, двигаясь параллельно самому себе. То есть распределение ускорений в базовой системе координат такое же, как и при вращении тела вокруг неподвижной оси. На рис. 88 показан случай, когда ускоренное вращение происходит против хода часов, а остальные оси базовой и связанной с телом систем координат не показаны.

Очевидно, что a_A является ускорением полюса или ускорением поступательного движения базовой системы координат и тела совместно с полюсом. Согласно векторным формулам для ускорений точек тела при вращательном движении вектор касательного ускорение вращения вокруг полюса равен

(7)

он перпендикулярен радиусу вращения AB и направлен в сторону углового ускорения, а его величина равна

(8)

Вектор нормального ускорения равен

(9)

он направлен по радиусу вращения AB от точки B к полюсу A, а его величина равна

(10)

При вычислении величин векторов в формулах (8) и (10) учитывалось, что векторы ρ и V_BA лежат в плоскости движения, а векторы ω и ε перпендикулярны ей (рис.88).

Подставляя формулы (7) и (9) в выражение для a_B , получаем

ДИНАМИКА