- •Аксиомы статики
- •Связи и их реакции
- •Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.
- •Момент силы относительно центра
- •Момент силы относительно оси. Аналитический и геометрический способы.
- •Пара сил. Теорема о сумме моментов сил пары относительно произв. Центра.
- •Теоремы о парах.
- •Лемма о параллельном переносе силы (лемма Пуансо)
- •Основная теорема статики
- •Условия равновесия твердого тела под действием произвольной плоской и пространственной системы сил.
- •Законы трения скольжения. Равновесие при наличии трения скольжения.
- •Трение качения. Равновесие при наличии трения качения.
- •Определение первого и второго статических инвариантов. Частные случаи приведения произвольной системы сил к центру.
- •Теорема Вариньона в векторной и скалярной формах
- •Центр тяжести. Основные методы.
- •Метод интегрирования.
- •Метод симметрии.
- •Метод разбиения.
- •Методы отрицательных весов, объемов и площадей.
- •Способы задания движения точки
- •Определение скорости и ускорения точки при векторном способе задания движения.
- •Координатном
- •Естественном
- •Поступательное движение тела. Теорема о траекториях, скоростях, ускорениях точек тела. Уравнение поступательного движения.
- •Вращательное движения твердого тела. Понятие угловой скорости и ускорения.
- •Определение скоростей и ускорений вращающегося предмета. Формула Эйлера.
- •Понятие сложного, абсолютного, относительного и переносного движений.
- •Теорема о сложении скоростей при сложном движении.
- •Теорема о сложении ускорений при сложном движении. (т. Кориолиса)
- •Ускорение Кориолиса. Способы вычисления.
- •Плоскопараллельное движение.
- •Теорема о скоростях точек тела при его плоском движении и следствия о проекциях скоростей двух его точек на ось, проходящую через 2 эти точки.
- •Мгновенный центр скоростей. Способы нахождения.
- •Теорема об ускорениях точек тела при плоском движении и следствия о проекциях ускорений двух его точек на ось, проходящую через 2 эти точки.
- •Законы динамики
- •Основное уравнение динамики. Дифференциальные уравнения движения м.Т. В проекциях на декартовые и естественные оси. Первая и вторая задача динамики.
- •Основное уравнение динамики относительного движения. Инерциальная система отсчета.
- •Прямолинейные колебания м.Т. Классификация сил, действующих на м.Т. При колебании.
- •Свободные колебания в среде без сопротивления.
- •Свободные колебания в среде с сопротивлением
- •Случай малого сопротивления
- •Случай критического сопротивления
- •Случай большого сопротивления
- •Механическая система. Диффуры движения механической системы.
- •Центр масс, формулы.
- •Теорема о движении центра масс. Следствия.
- •Меры движения: количество движения м.Т. И механической системы, кинетический момент м.Т. И механической системы относительно центра и оси, кинетическая энергия м.Т. И мех. Системы.
- •Меры действия сил: элементарный импульс силы
- •Кинетическая энергия
- •Теорема об изменении количества движения механической системы в диф. И интегральной форме. Следствия.
- •Момент инерции относительно оси. Радиус инерции. Формулы.
- •Теорема об изменении кинетического момента мех.Системы в векторной, скалярной форме. Следствия
- •Диффуры поступательного, вращательного и плоского движения.
- •Теорема об изменении кинетической энергии в диф. И интегральной форме.
- •Теорема Штейнера-Гюйгенса
- •Сила инерции. Принцип Даламбера для м.Т.
- •Приведение системы сил инерции к простейшему виду при поступательном, вращательном и плоском движении.
- •Принцип виртуальных перемещений.
- •Общее уравнение динамики.
- •Обобщенные координаты и скорости. Число степеней свободы.
- •Обобщенные силы и способы вычисления.
- •Условия равновесия механической системы в обобщенных координатах.
- •Для консервативных механических систем необходимым и достаточным условием равновесия является система равенств:
- •Уравнение Лагранжа второго рода.
Основное уравнение динамики относительного движения. Инерциальная система отсчета.
Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид
где a – абсолютное ускорение точки;
Fi – силы, действующие на точку, включая реакции связей.
Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного aпер , относительного aотн и кориолисова aкор , т.е.
Подставляя это выражение в (7.1), получим
или
Введем в рассмотрение два вектора
и назовем их переносной и кориолисовой силами инерции.
Подставим эти векторы в уравнение (7.2):
Уравнение (7.3) представляет собой основное уравнение динамики относительного движения материальной точки.
Инерциальная система отсчета - система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения. Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Все инерциальные системы отсчета равноправны, т. е. во всех таких системах законы физики одинаковы.
Прямолинейные колебания м.Т. Классификация сил, действующих на м.Т. При колебании.
 Пусть
точка М массой m
притягивается к точке O
силой
Пусть
точка М массой m
притягивается к точке O
силой
![]() ,
пропорциональной расстоянию OM,
а начальная скорость точки
направлена вдоль прямой OM
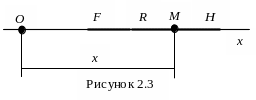
или равна нулю (рис. 2.3). В этом случае
точка M движется
прямолинейно, а ее положение определяется
одной координатой x,
отсчитываемой от положения равновесия
(точки O). Проекция
восстанавливающей силы
на ось x:
,
пропорциональной расстоянию OM,
а начальная скорость точки
направлена вдоль прямой OM
или равна нулю (рис. 2.3). В этом случае
точка M движется
прямолинейно, а ее положение определяется
одной координатой x,
отсчитываемой от положения равновесия
(точки O). Проекция
восстанавливающей силы
на ось x:
![]() ,
где с – коэффициент пропорциональности,
с > 0.
,
где с – коэффициент пропорциональности,
с > 0.
Пусть на точку M
действует также сила сопротивления
![]() ,
пропорциональная скорости этой точки
и направленная противоположно ей.
Проекция силы на ось x:
,
пропорциональная скорости этой точки
и направленная противоположно ей.
Проекция силы на ось x:
![]() ,
где β – коэффициент пропорциональности,
β > 0. Кроме того, на точку M
действует гармоническая возмущающая
сила
,
где β – коэффициент пропорциональности,
β > 0. Кроме того, на точку M
действует гармоническая возмущающая
сила
![]() ,
направленная вдоль прямолинейной
траектории точки. Проекция этой силы
на ось x:
,
направленная вдоль прямолинейной
траектории точки. Проекция этой силы
на ось x:
![]() ,
где
,
где
![]() – амплитуда возмущающей силы,
> 0; р – ее частота.
– амплитуда возмущающей силы,
> 0; р – ее частота.
Запишем дифференциальное уравнение движения точки М
![]()
или
![]() .
.
Разделим обе части этого уравнения на m, введем обозначения
![]()
и получим уравнение
![]() ,
,
которое является неоднородным линейным дифференциальным уравнениям с постоянными коэффициентами.
Восстанавливающие силы, стремящиеся вернуть точку в положение равновесия. Они зависят от величины отклонения точки от положения равновесия и направлены в сторону, противоположную отклонению. Именно эти силы придают движению точки колебательный характер.
Силы сопротивления, зависящие от скорости движения. Это силы трения скольжения, силы сопротивления и др
Возмущающие силы, являющиеся заданными функциями времени.
Свободные колебания в среде без сопротивления.
Рассмотрим колебания материальной точки, происходящие под действием одной восстанавливающей силы . Такие колебания называют свободными и описывают однородным дифференциальным уравнением, которое можно получить из дифференциального уравнения прямолинейных колебаний материальной точки ( ), положив n = 0 и h = 0,
![]()
Характеристическое уравнение этого
дифференциального уравнения
![]() имеет
чисто мнимые корни
имеет
чисто мнимые корни
![]() ,
поэтому общее решение уравнения запишем
в виде:
,
поэтому общее решение уравнения запишем
в виде:
![]()
где С1 и С2 – постоянные интегрирования, определяемые из начальных условий:
![]()
Продифференцируем функцию
![]()
Получим
![]() .
.
Подставив С1 и С2 в уравнение, запишем закон движения точки
![]()
и преобразуем его к более удобному виду. Введя обозначения
![]()
Получим
![]()
или
![]()
Таким образом, свободные колебания
материальной точки в среде без
сопротивления являются гармоническими.
Амплитуда этих колебаний равна А,
фаза
![]() ,
где
,
где
![]() – начальная фаза. Величину
– начальная фаза. Величину
![]() называют круговой или циклической
частотой колебаний. Период колебаний
называют круговой или циклической
частотой колебаний. Период колебаний
![]() является периодом функции
является периодом функции
![]() .
Последнее соотношение показывает, что
круговая частота k
равна числу полных колебаний точки за
2π секунд: k = 2π/T.
Таким образом, частота и период
гармонических колебаний зависят от
массы точки и коэффициента пропорциональности
восстанавливающей силы, но не зависят
от начальных условий. Это свойство
свободных колебаний называют изохронностью.
Амплитуда и начальная фаза зависят как
от параметров системы m
и c, так и от начальных
условий.
.
Последнее соотношение показывает, что
круговая частота k
равна числу полных колебаний точки за
2π секунд: k = 2π/T.
Таким образом, частота и период
гармонических колебаний зависят от
массы точки и коэффициента пропорциональности
восстанавливающей силы, но не зависят
от начальных условий. Это свойство
свободных колебаний называют изохронностью.
Амплитуда и начальная фаза зависят как
от параметров системы m
и c, так и от начальных
условий.