15. Теорема об изменении кинетического момента мех.Системы в векторной, скалярной форме. Следствия

Рассмотрим систему, состоящую из N материальных точек, и запишем для каждой из них соотношение ( )

,

Где – равнодействующие всех внешних и внутренних сил, приложенных к j-й точке системы.

Сложим почленно полученные уравнения:

Из 2-го свойства внутренних сил следует, что . Преобразуя левую часть уравнения

получим из него

где – главный момент внешних сил системы относительно центра О.

Итак, доказана следующая теорема. Производная по времени от кинетического момента механической системы относительно неподвижного центра равна главному моменту внешних сил системы относительно того же центра.

Векторному уравнению соответствуют три уравнения в проекциях на оси координат:

где – главные моменты внешних сил относительно осей x, y, z. Следует отметить, что уравнения этого вида рекомендуется использовать при рассмотрении системы, в состав которой входит тело, вращающееся вокруг неподвижной оси. Тогда, совмещая одну из координатных осей с осью вращения, получим уравнение, не содержащее неизвестных реакций опор вращающегося тела.

16. Диффуры поступательного, вращательного и плоского движения.

Рассмотрим тело, вращающееся вокруг неподвижной оси z с угловой скоростью ω. На него действуют система внешних сил ( ) и реакции опор (рис. 6.6). Чтобы исключить из рассмотрения неизвестные реакции , запишем 3-е уравнение системы ( ):

П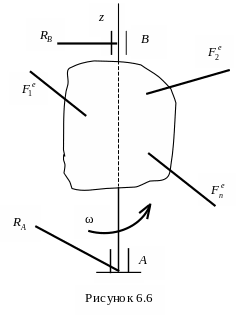 оскольку в соответствии с формулой , из уравнения получим

или

,

где φ – угол поворота тела.

Сравнивая последнее уравнение с дифференциальными уравнениями движения центра масс ( ), применяемыми для описания поступательного движения тела, приходим к выводу об аналогичности структур этих уравнений. Поскольку масса характеризует инертность тела, совершающего поступательное движение, момент инерции является мерой инертности тела, вращающегося вокруг неподвижной оси.

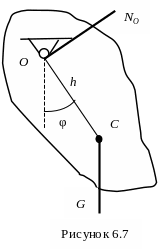
Рассмотрим в качестве примера движение под действием силы тяжести физического маятника, т.е. тела, имеющего горизонтальную ось вращения, которая не проходит через центр масс тела С (рис. 6.7). Обозначим через силу тяжести физического маятника, – реакцию его оси, h – расстояние от оси вращения до центра масс тела. Совместим ось z с осью вращения тела и запишем дифференциальное уравнение вращательного движения

или

, (6.24)

где – момент инерции физического маятника относительно оси вращения.

17. Теорема об изменении кинетической энергии в диф. И интегральной форме.

Рассмотрим некоторое перемещение системы, состоящей из N материальных точек, и запишем для каждой из них соотношение ( )

где – суммы работ внешних и внутренних сил, действующих на j -ю точку системы. Сложим почленно уравнения

Это уравнение выражает теорему об изменении кинетической энергии системы в интегральной форме. Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ всех внешних и внутренних сил, действующих на точки системы, на том же перемещении.

Положим в этом уравнении , где Т – кинетическая энергия системы в текущем положении, и продифференцируем его по времени. Тогда, учитывая ( ), где , получим

Таким образом, получена дифференциальная форма теоремы. Производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы.

Соотношения ( ) и ( ), в отличие от ранее рассмотренных общих теорем динамики, описывают зависимость изменения кинетической энергии от внутренних сил. Однако чаще всего механические системы моделируют твердыми телами, соединенными между собой с помощью внутренних связей. Их реализуют в виде шарниров без трения, гибких нерастяжимых нитей или осуществляют за счет относительного качения без проскальзывания. Такие системы называют неизменяемыми. Сумма работ (и мощностей) внутренних сил неизменяемой системы равна нулю, а соотношения принимают вид:

;