6. Свободные колебания в среде с сопротивлением

Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы и силы сопротивления. Дифференциальное уравнение такого движения получим, воспользовавшись , при h = 0

.

Его характеристическое уравнение имеет корни

.

Характер движения точки существенно зависит от соотношения величин n и k. Рассмотрим три возможных случая этого соотношения.

Случай малого сопротивления

Корни характеристического уравнения комплексно сопряженные: , где . Общее решение дифференциального уравнения имеет вид:

,

где постоянные интегрирования С₁ и С₂ определяют из начальных условий.

Введем новые постоянные А и φ₀ с помощью соотношений

,

тогда из уравнения получим

. (2.14)

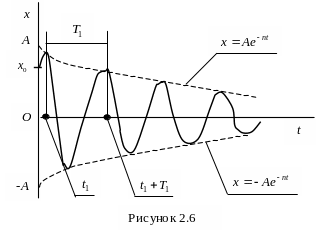
Это уравнение описывает затухающие колебания, график которых приведен на рис. 2.6. Они не являются периодическими, но промежуток времени между двумя последовательными максимальными отклонениями точки от положения равновесия в одну и ту же сторону остается неизменным. Эту величину условно называют периодом затухающих колебаний: , где k₁ – частота затухающих колебаний.

Скорость затухания колебаний характеризуется отношением величин двух последовательных максимальных отклонений точки от положения равновесия в одну и ту же сторону

,

которое называют декрементом колебаний. Используют также натуральный логарифм этой величины , называемый логарифмическим декрементом колебаний. Поскольку частота затухающих колебаний меньше частоты незатухающих колебаний k, появление силы сопротивления приводит к увеличению периода колебаний: . Это изменение может быть весьма незначительным и поэтому основным влиянием, которое оказывает сила сопротивления на свободные колебания, является качественное изменение характера колебаний, которые становятся затухающими.

Случай критического сопротивления

Корни характеристического уравнения вещественные, равные и отрицательные , а общее решение дифференциального уравнения имеет вид:

.

Случай большого сопротивления

Корни характеристического уравнения вещественные, отрицательные и различные, а общее решение дифференциального уравнения имеет вид:

.

В двух последних случаях движение точки теряет колебательный характер и становится апериодическим. В зависимости от величины и направления начальной скорости график колебаний имеет вид одной из трех кривых, приведенных на рис. 2.7.

7. Механическая система. Диффуры движения механической системы.

Механической системой называют любую совокупность материальных точек. В частности, любое твердое тело, которое можно представить как совокупность его частиц, образует механическую систему.

8. Центр масс, формулы.

Масса механической системы равна сумме масс материальных точек, образующих эту систему:

где N – число всех точек системы.

Центром масс механической системы называют геометрическую точку, радиус-вектор которой и декартовы координаты :

где – радиус-вектор и координаты j-й точки системы.