18. Теорема Штейнера-Гюйгенса

момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

где

— известный момент инерции относительно оси, проходящей через центр масс тела,

— искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

Момент инерции, по определению:

Радиус-вектор можно расписать как разность двух векторов:

,

где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

Вынося за сумму , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Тогда:

Откуда и следует искомая формула:

,

где — известный момент инерции относительно оси, проходящей через центр масс тела.

19. Сила инерции. Принцип Даламбера для м.Т.

Методом кинетостатики называют общий метод решения задач динамики, при использовании которого уравнения движения принимают вид уравнений равновесия статики.

Рассмотрим материальную точку, движущуюся под действием системы сил , и запишем для нее основное уравнение динамики

.

Введем в рассмотрение вектор

,

направленный противоположно ускорению точки и равный по величине произведению массы точки на модуль ее ускорения. Этот вектор называют силой инерции материальной точки. Теперь основному уравнению динамики точки можно придать следующий вид:

.

Приложим условно силу инерции к материальной точке, тогда уравнение будет представлять собой необходимое и достаточное условие равновесия сходящейся системы сил ( ). Это условие является содержанием принципа Даламбера для материальной точки. Если к движущейся материальной точке условно приложить силу инерции, то в любой момент времени действующие на точку силы и сила инерции образуют уравновешенную систему сил.

Уравнениями метода кинетостатики в данном случае являются уравнения равновесия полученной сходящейся системы сил:

20. Приведение системы сил инерции к простейшему виду при поступательном, вращательном и плоском движении.

Главный вектор сил инерции не зависит от выбора центра приведения и при любом движении тела может быть определен соотношением ( ). Определим главный момент сил инерции для некоторых случае движения твердого тела.

Поступательное движение

П ри поступательном движении тела ускорения всех его точек в данный момент времени одинаковы и равны ускорению центра масс (рис. 8.2).

Сила инерции материальной точки массой будет равна

.

Выберем в качестве центра приведения центр масс тела и вычислим главный момент сил инерции

так как радиус-вектор центра масс относительно центра масс равен нулю.

Таким образом, при поступательном движении тела силы инерции его точек приводятся к равнодействующей, условно приложенной в центре масс тела и равной главному вектору сил инерции .

Вращение вокруг неподвижной оси

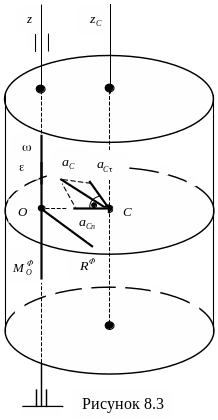Рассмотрим твердое тело, имеющее плоскость материальной симметрии и вращающееся вокруг неподвижной оси z, перпендикулярной этой плоскости и не проходящей через центр масс тела С, как показано на рис. 8.3. Приведем силы инерции к центру О, в котором ось вращения пересекает плоскость симметрии. Тогда, вследствие симметрии тела, сила и пара сил, к которым приводят силы инерции, лежат в плоскости симметрии. Сила равна главному вектору сил инерции . Момент пары сил направлен перпендикулярно плоскости симметрии, т.е. вдоль оси вращения, противоположно вектору углового ускорения . Его проекцию на ось вращения получим из формул ( ) и ( )

(8.14)

где – момент инерции тела относительно оси вращения.

Если ось вращения проходит через центр масс тела (см. рис. 8.3, ось ), то ускорение центра масс и главный вектор сил инерции . Силы инерции в этом случае эквивалентны паре сил, проекция момента которой

Плоское движение

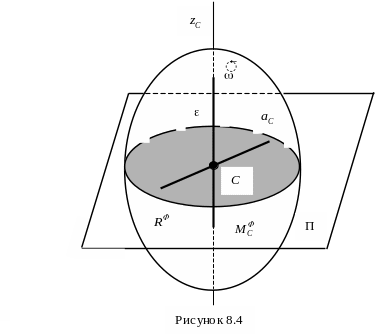
Пусть тело имеет плоскость материальной симметрии и движется так, что эта плоскость все время совпадает с некоторой неподвижной плоскостью П (рис. 8.4). Разложим движение тела на поступательное, определяемое движением центра масс С, и вращательное вокруг оси , проходящей через центр масс тела перпендикулярно плоскости симметрии. Силы инерции поступательного движения приведем к силе , приложенной в центре масс С, а силы инерции вращательного движения – к паре сил, лежащей в плоскости симметрии. Проекция момента этой пары на ось :

.

21. Классификация связей: голономные, стационарные и удерживающие. Виртуальное перемещение точки. Виртуальная работа. Идеальная связь.

    Связь называется голономной, если в уравнение связи входят только координаты точек механической системы или иные параметры, определяющие ее положение в пространстве.

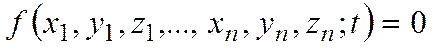
Связь называют удерживающей, если она выражается математически равенством, и неудерживающей, если она выражается неравенством.

Связь называется стационарной, если в уравнение связи время явно не входит. Если в уравнение связи время входит явным образом, то связь − нестационарная.

Примером нестационарной связи, наложенной на материальную точку, является нить, длина которой изменяется согласно некоторому закону . Это голономная, неудерживающая, нестационарная связь.

Виртуальным (возможным) перемещением точки (обозначается ) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями.

Проекции вектора виртуального перемещения точки называются вариациями координат.

 В случае голономной нестационарной связи уравнение в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности и вариации координат удовлетворяют уравнению ,

выражающему перпендикулярность вектора нормали к поверхности и вектора .

Виртуальным перемещением механической системы называется совокупность виртуальных перемещений точек этой системы.

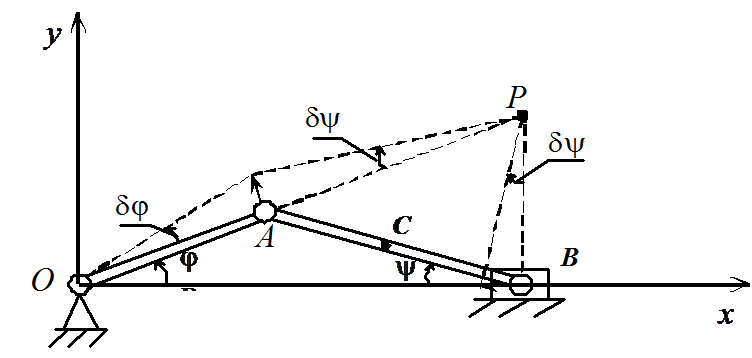
 Например, виртуальным перемещением кривошипно-ползунного механизма, являются два элементарных поворота – кривошипа на угол вокруг оси вращения и шатуна на угол вокруг мгновенного центра скоростей. Из геометрических соображений следует, что: . Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.

 

 

Виртуальной работой силы (обозначается ) называется работа силы на виртуальном перемещении точки ее приложения, т.е.: .

Связь называется идеальной, если сумма работ реакций этой связи на любом виртуальном перемещении системы равна нулю.

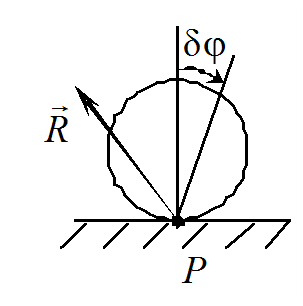Примером является шероховатая поверхность для катка, катящегося без скольжения, при отсутствии трения качения .