Теорема о движении центра масс. Следствия.
Преобразуем равенство
,
подставив в него количество движения
системы в виде (
)
.
Учитывая, что масса системы постоянна, получим
или
.
(5.22)
Сравнивая это уравнение с основным
уравнением динамики точки (
),
приходим к следующей формулировке
теоремы о движении центра масс:
Центр масс механической системы
движется как материальная точка, в
которой сосредоточена вся масса системы
и к которой приложены все внешние силы,
действующие на систему.
Спроецируем уравнение (5.22) на оси неподвижной декартовой системы координат и получим дифференциальные уравнения движения центра масс:
.
Сформулируем следствия из теоремы.
1) Внутренние силы не влияют непосредственно на движение центра масс системы, но могут оказывать косвенное влияние через внешние силы.
2) Если главный вектор внешних сил, действующих на систему, на рассматриваемом интервале времени равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно.
Положим в уравнении (5.22)
,
тогда ускорение центра масс
,
т.е. его скорость
.
При этом, если начальная скорость центра
масс
,
то центр масс находится в покое, а если
,
то центр масс движется равномерно и
прямолинейно с этой скоростью.
3) Если проекция главного вектора внешних сил системы на некоторую неподвижную ось на рассматриваемом интервале времени равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.
Положив в 1-м уравнении (
)
,
получим, что
,
т.е.
.
Если при этом в начальный момент времени
проекция скорости центра масс
,
то
,
т.е. центр масс не движется вдоль оси х.
Остановимся на этом случае подробнее.
Предположим, что в начальный момент
времени
абсциссы точек системы были равны
,
а в момент времени
стали равны
.
Поскольку в рассматриваемом случае
,
из формул (
),
определяющих координаты центра масс,
следует
,
откуда после преобразований получим
Меры движения: количество движения м.Т. И механической системы, кинетический момент м.Т. И механической системы относительно центра и оси, кинетическая энергия м.Т. И мех. Системы.
Количеством движения системы называют векторную величину Q, равную геометрической сумме (главному вектору) количеств движения всех точек системы
Количество движения системы равно произведению массы всей системы на скорость её центра масс
Если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела (системы) равно нулю
При сложном движении количество движения не будет зависеть от его вращательного движения вокруг центра масс
Таким образом, количество движения тела можно рассматривать как характеристику поступательного движения тела
При сложном движении – как характеристику поступательной части движения вместе с центром масс тела
К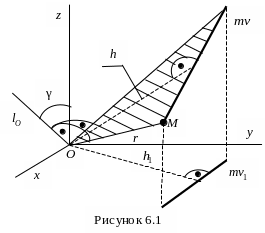
инетический
момент материальной точки М относительно
неподвижного центра О – это величина,
равная векторному произведению
радиус-вектора этой точки, проведенного
из центра О, на ее количество движения
(рис. 6.1):
Векторное произведение в правой части
представляет собой момент вектора
относительно центра О, отсюда 2-е
название вектора
– момент количества
движения,
.
Вектор направлен перпендикулярно плоскости, проходящей через вектор и центр О, в ту сторону, откуда вектор виден направленным против часовой стрелки относительно этого центра. Его модуль:
где h – плечо вектора относительно центра О.
Кинетический момент материальной точки относительно неподвижной оси равен проекции на эту ось кинетического момента точки относительно любого центра, выбранного на данной оси
Определение кинетического момента относительно оси аналогично вычислению соответствующего момента силы – спроецируем вектор на плоскость, перпендикулярную оси, и определим алгебраический момент проекции относительно точки пересечения оси и плоскости
Кинетический момент
,
если, глядя с положительного направления
оси z, видим вектор
направленным против часовой стрелки
относительно центра О.
Кинетический момент (главный момент количеств движения) механической системы относительно неподвижного центра О равен сумме кинетических моментов всех материальных точек системы относительно этого центра:
Аналогично определяют кинетический момент системы относительно неподвижной оси:
О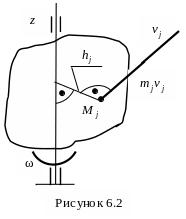
пределим
кинетический момент твердого тела
относительно неподвижной оси вращения
z (рис. 6.2). Обозначив
через
расстояние от точки
до оси вращения, вычислим кинетический
момент точки относительно оси z
,
а также кинетический момент тела
По определению,
полученная сумма является моментом
инерции тела относительно оси z:
,
поэтому из выражения (
)
получим
.
Таким образом, кинетический момент твердого тела относительно оси вращения равен произведению момента инерции тела относительно данной оси на проекцию его угловой скорости на ту же ось.
Кинетическая энергия материальной точки – это скалярная мера механического движения, равная половине произведения массы точки на квадрат ее скорости:
Кинетическая энергия механической системы – это сумма кинетических энергий всех материальных точек, образующих систему:
Кинетическая энергия является неотрицательной величиной, она равна нулю только в том случае, если неподвижны все точки системы. Однако и кинетическая энергия не является универсальной мерой движения, так как, будучи величиной скалярной, не отражает направление движения.