Ряды «эталоны»

1. Ряд Дирихле

(обобщенный гармонический ряд)

-

2. Геометрическая прогрессия

, .

П ризнак Даламбера. Пусть задан знакоположительный ряд . Тогда if , то

Р адикальный признак Коши. Пусть задан знакоположительный ряд . Тогда if , то

Интегральный признак Коши. Пусть для знакоположительного ряда $ положительная, непрерывная и монотонно убывающая на промежутке функция такая, что . Тогда ряд и сходятся или расходятся одновременно.

Знакопеременные ряды

Пусть задан знакопеременный ряд (1), где a_n – числа произвольного знака. Тогда, если ряд (2) сходится, то сходится и данный ряд, при этом он называется абсолютно сходящимся. Если ряд (2) расходится, а данный ряд (1) сходится, то он называется условно сходящимся.

Признак Лейбница. Пусть дан знакочередующийся ряд . Тогда, if выполняются условия: , то данный ряд сходится и его сумма .

Степенные ряды

или , if .

(-R, R) – интервал сходимости, при х=-R и х=R ряд исследуется дополнительно.

Ряд Фурье

,

, , .

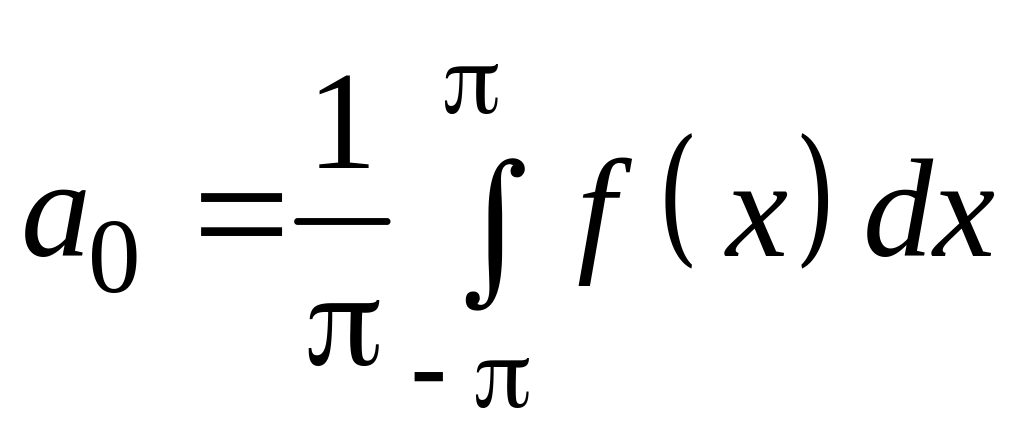Если 2 - периодическая функция f(х) кусочно-монотонная и ограниченная, то ряд справа сходится, именно, к этой функции f(х).

Если f(х) – четная функция, то она раскладывается в ряд Фурье только по косинусам, при этом , , ;

если f(х) – нечетная функция, то она раскладывается только по синусам, при этом , , .

Если – периодическая функция f(х) задана на , то ряд Фурье имеет вид:

, где

, , .

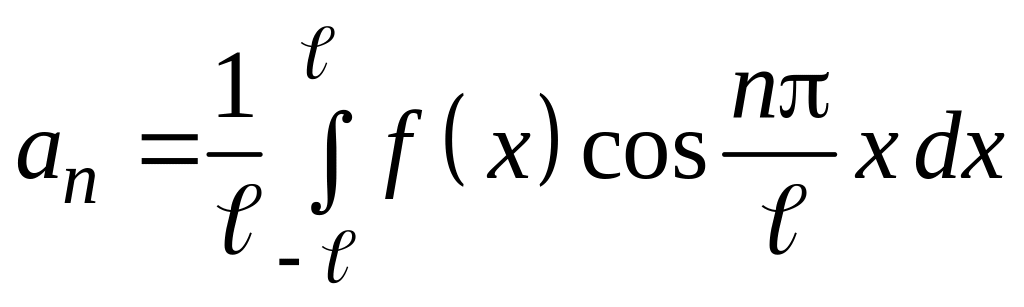КРАТКОЕ СОДЕРЖАНИЕ

ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

10.1. Числовые ряды. Сходимость и сумма ряда

Рассмотрим числовую последовательность

Определение 10.1.1. Бесконечная сумма

называется числовым рядом. Числа называются членами ряда, а число a_n – n-м членом или общим членом ряда.

Кратко числовой ряд обозначается символом .

Определение 10.1.2. Сумма конечного числа n первых членов ряда называется n-й частичной суммой ряда

.

Рассмотрим последовательность частичных сумм , где

,

,

…………..

,

,

………………………..

Определение 10.1.3. Числовой ряд называется сходящимся, если последовательность частичных сумм сходится к некоторому числу S, которое называется суммой этого ряда.

Итак, по определению, ряд сходится к сумме S, если . В этом случае пишут

.

Если предел последовательности не существует или равен бесконечности, то ряд называется расходящимся.

Пример 10.1.1. Рассмотрим ряд, составленный из членов геометрической прогрессии

Сумма ее n первых членов равна

.

1. Если , то при n  и, следовательно,

.

Значит, в случае ряд сходится и его сумма .

2. Если , то при n   и тогда при n  . Таким образом, при ряд расходится.

3. Если , то ряд имеет вид

,

в этом случае и , т.е. ряд расходится.

4. Если , то ряд имеет вид

В этом случае и предела не имеет  ряд расходится.

Таким образом, ряд , составленный из членов геометрической прогрессии, сходится, если , и расходится при .

Пример 10.1.2. Исследовать на сходимость ряд

.

Решение. Общий член этого ряда раскладывается на простейшие дроби следующим образом: . Тогда

.

Так как , то искомый ряд сходится и его сумма S=1.

Суммой двух рядов и называется ряд

.

Произведением ряда на действительное число  называется ряд .

Пусть ряд сходится к сумме S. Перепишем равенство в виде и обозначим Это выражение, представляющее собой новый ряд, называется остатком ряда . Таким образом, для сходящегося ряда имеет равенство

.

Справедлива следующая теорема.

Теорема 10.1.1. Для того, чтобы ряд сходился необходимо и достаточно, чтобы .

Доказательство теоремы вытекает из определения суммы ряда и равенства .