10.6. Знакочередующиеся ряды. Признак Лейбница

До сих пор мы рассматривали ряды, члены которых положительны. Сейчас будем рассматривать ряды, члены которых имеют чередующиеся знаки, т.е. ряды вида

, где а₁, а₂, …, а_n, … – положительны.

Теорема 10.6.1 (Лейбница). Если в знакочередующемся ряде

члены таковы, что выполняются два условия:

1. 

2. ,

то ряд сходится, его сумма положительна и не превосходит первого члена.

Доказательство. Рассмотрим сумму n = 2m первых членов ряда .

Из условия следует, что выражение в каждой скобке положительно. Следовательно, сумма положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:

.

В силу условия каждая из скобок положительна. Поэтому в результате вычитания этих скобок из а₁ мы получим число, меньшее а₁, т.е. .

Таким образом, мы установили, что при возрастании m возрастает и ограничена сверху. Отсюда следует, что 

, причем 0 < S < a₁.

Докажем теперь, что «нечетные» частичные суммы также стремятся к пределу S . Очевидно,

.

Так как по условию , то

.

Тем самым мы доказали, что как при четном n, так и при нечетном. Следовательно, ряд сходится.

Замечание 10.6.1. Теорема Лейбница справедлива, если неравенства выполняются, начиная с некоторого N.

Пример 10.6.1. Ряд сходится, так как

1. ;

2. .

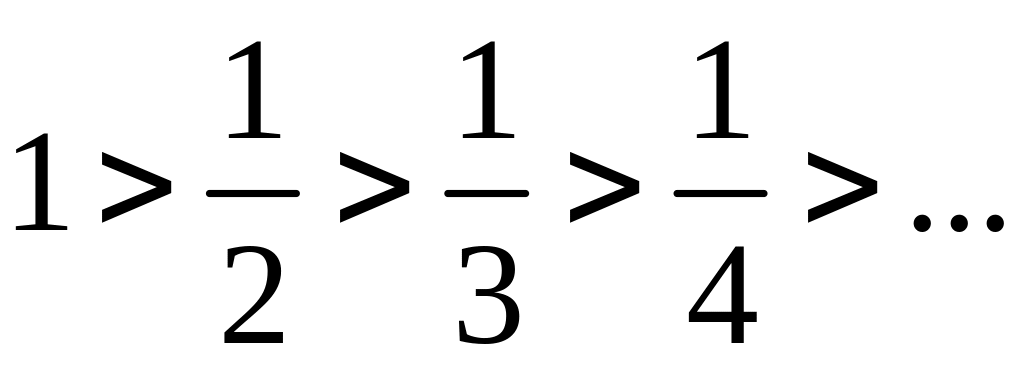Пример 10.6.2. Ряд сходится по теореме Лейбница, так как

1. ;

2. .

Рассмотрим теперь остаток ряда , представляющий собой новый знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница. Тогда его сумма на основании теоремы удовлетворяет неравенству

.

Ряд, удовлетворяющий условиям теоремы , называют рядом Лейбница. Формула дает оценку остатка ряда Лейбница.

Пример 10.6.3. Установить сходимость ряда и найти его сумму с точностью до 0,01.

Решение. Данный ряд сходится, как ряд Лейбница. Согласно неравенству имеем . Неравенство справедливо, начиная с n = 4, т.е. сумма ряда

.

10.7. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Рассмотренные в п.10.6 знакочередующиеся ряды являются, очевидно, частным случаем знакопеременных рядов.

Дадим один важный достаточный признак сходимости знакопеременного ряда.

Теорема 10.7.1. Если знакопеременный ряд

таков, что ряд, составленный из абсолютных величин его членов,

сходится, то и данный знакопеременный ряд также сходится.

Доказательство. Пусть и – суммы n первых членов рядов и .

Пусть, далее, – сумма всех положительных, а – сумма абсолютных величин всех отрицательных членов среди первых n членов ряда ; тогда

, .

По условию ; и – положительные возрастающие величины, меньшие . Следовательно, и . Из соотношения следует, что

,

т.е. знакопеременный ряд сходится.

Доказанная теорема дает возможность судить о сходимости некоторых знакопеременных рядов. Исследование вопроса о сходимости сводится в этом случае к исследованию рядов с положительными членами.

Пример 10.7.1. Исследовать сходимость ряда

где   любой угол (в зависимости от  может иметь любой знак).

Решение. Рассмотрим два ряда:

и

Ряд сходится, как ряд Дирихле (р = 3 > 1). Члены ряда не больше соответственных членов ряда (так как ); следовательно, ряд тоже сходится по первому признаку сравнения. Но тогда в силу доказанной теоремы данный знакопеременный ряд тоже сходится.

Заметим, что этот признак сходимости является только достаточным признаком сходимости, но не необходимым: существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся.

Пример 10.7.2. Ряд сходится по теореме Лейбница, хотя ряд из абсолютных величин его членов является гармоническим и, как известно, расходится.

В связи с этим полезно ввести понятие об абсолютной и условной сходимости знакопеременных рядов и на основе этих понятий классифицировать знакопеременные ряды.

Определение 10.7.1. Знакопеременный ряд

называется абсолютно сходящимся, если сходится ряд

Если же знакопеременный ряд сходится, а ряд расходится, то данный ряд называется условно, или неабсолютно, сходящимся рядом.

Таким образом, ряд , рассмотренный в примере 10.7.2, условно сходящийся, а ряд абсолютно сходящийся.

Пример 10.7.3. Знакопеременный ряд

есть ряд абсолютно сходящийся, так как ряд из абсолютных величин его

,

как было показано в п.10.5 при помощи признака Даламбера, сходится.