10.12. Разложение по степеням х функций

, sin x, cos x,

Рассмотрим примеры разложения некоторых функций в ряд Маклорена.

1. , а = 0.

Так как , а , то

,

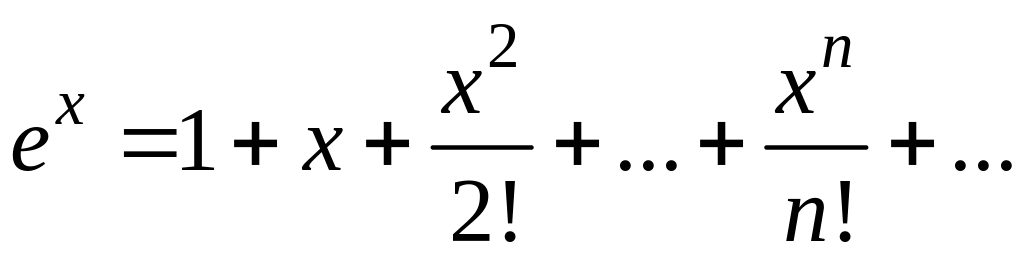где .

Покажем, что для любого х. Для этого рассмотрим степенной ряд и покажем, что он абсолютно сходится для всех . Действительно, .

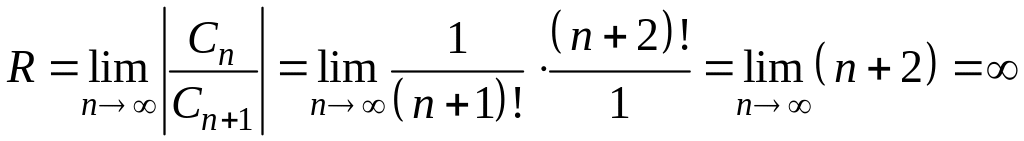Так как ряд сходится для всех х, то из необходимого признака сходимости следует, что для всех .

Функция для всех х  0 удовлетворяет неравенству

.

Если , то , так как 0 <  < 1.

Тогда , как произведение функции ограниченной на бесконечно малую.

Следовательно, для всех значений х полученный ряд Маклорена сходится и представляет функцию .

2. , а = 0.

, ,

, , …,

.

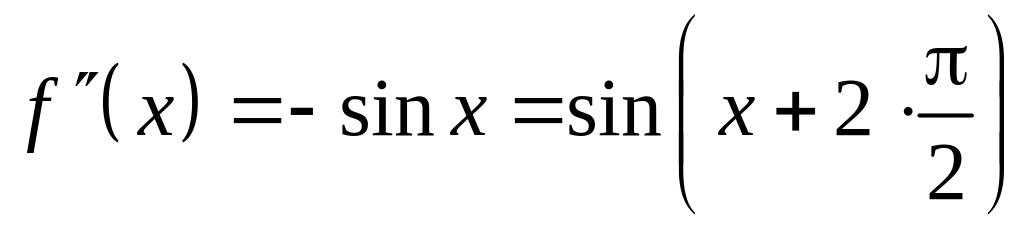Тогда , , , , , … и мы имеем разложение в ряд Маклорена

,

где (С находится между 0 и х).

, так как , а .

3. , а = 0.

Аналогично, как в предыдущем примере, получаем

,

где (С находится между 0 и х).

Очевидно, .

4. Биномиальный ряд и его частные случаи.

Разложим в ряд Маклорена функцию , где m - произвольное постоянное число.

Здесь оценка остаточного члена представляет некоторые трудности, и потому к оценке условий разложимости подойдем несколько иначе.

Сначала формально найдем коэффициенты разложения в ряд Маклорена. ;  ;

 ;

  ,

………………………………………………,

.

Поэтому

Этот ряд называется биномиальным, найдем его интервал сходимости.

.

Значит, ряд сходится абсолютно при . Покажем, что суммой этого ряда является .

В самом деле, нетрудно проверить, что функция f(x), определяемая биномиальным рядом, является решением задачи Коши для дифференциального уравнения , f(0)=1. Но решением этой же задачи является функция , так как и  . Отсюда в силу единственности решения задачи Коши получаем , , т.е. биномиальный ряд сходится абсолютно в интервале (1, 1) к . На концах интервала для некоторых т ряд сходится, для некоторых  расходится, об этом сказано в практической части модуля.

Заметим, что если m – целое положительное число, то биномиальный ряд превращается в бином Ньютона.

Рассмотрим частные случаи биномиального ряда:

1. при m = 1 получаем

;

2. при m = имеем

;

3. при m = 

Применим разложение биномиального ряда к разложению других функций. Разложим в ряд Маклорена функцию .

Подставляя в последнее равенство вместо х выражение , получим

На основании теоремы об интегрировании степенных рядов получаем:

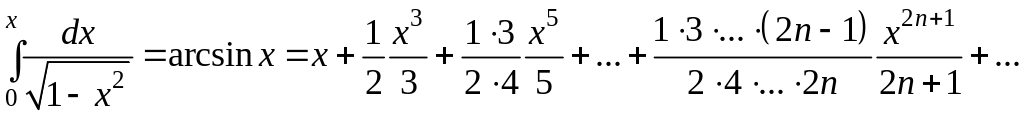
Этот ряд сходится для .

10.13. Приложение рядов к приближенным вычислениям

Приближенное вычисление значений функций

Допустим, что функция f(x) в окрестности точки х₀ разлагается в ряд Тейлора. Тогда точное ее значение f(x₀) может быть вычислено по ряду Тейлора, а приближенное ее значение – по частичной сумме этого ряда. Возникающую при этом ошибку можно оценивать при помощи остаточного члена , либо непосредственно оценивая остаток ряда. Если получился числовой ряд знакочередующимся, то по теореме Лейбница ошибка не превышает первого отброшенного члена ряда, взятого по абсолютной величине; в случае знакоположительного ряда  подбирают другой ряд (обычно геометрическую прогрессию), члены которого больше членов остатка и сумму которого можно найти.

Пример 10.13.1. Вычислить с точностью до 10^-4.

Решение. Имеем . Воспользуемся биномиальным рядом при , .

Получили знакочередующийся ряд, остаток которого не превышает первого отброшенного члена. Так как , то с указанной точностью , так что .

Пример 10.13.2. Вычислить число е с точностью 10^-5.

Решение. . Пусть х = 1.

.

Остаточный член имеет вид (0<<1).

Тогда .

Решая подбором n последнее неравенство, получим n = 8, т.е.

.

Покажем, как можно оценивать ошибку, пользуясь остатком ряда.

.

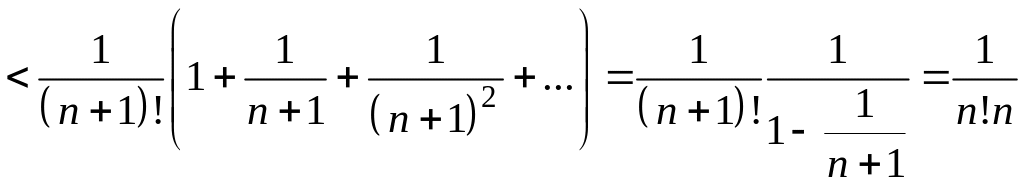Получилась оценка в три раза более точная, чем .

Вычисление определенных интегралов

Существуют определенные интегралы, у которых первообразные от подынтегральных функций не выражаются через элементарные функции. Такие интегралы иногда удобно вычислять приближенно с помощью рядов. Покажем на примере, как это делается.

Пример 10.13.3. Вычислить .

Решение. Здесь первообразная от не является элементарной функцией. Используем разложение (- < x < ).

Пусть , тогда (- < x < ), а

С помощью этого равенства можно для любого а вычислить данный интеграл с любой заданной точностью.

Применение рядов к решению дифференциальных уравнений

Если интегрирование дифференциального уравнения не сводится к квадратурам, то прибегают к приближенным методам. Одним из таких методов является представление решения в виде ряда Тейлора; сумма конечного числа членов этого ряда будет приближенно равняться искомому частному решению.

Пусть, например, требуется найти решение дифференциального уравнения второго порядка

,

удовлетворяющее начальным условиям

.

Допустим, что решение у = f(x) существует и представимо в виде ряда Тейлора

Нам нужно найти f(x₀), f(x₀), f''(x₀), …. Это можно сделать при помощи условий и уравнения .

Действительно, из условий следует

;

из уравнения получаем

.

Дифференцируя обе части уравнения по х, получим

и, подставляя значения , , и , получаем

.

Дифференцируя соотношение еще раз, найдем

и.т.д.

Найденные значения производных подставляем в равенство . Для тех значений х, для которых этот ряд сходится, он представляет решение уравнения.

Пример 10.13.4. Найти решение уравнения , удовлетворяющее начальным условиям у(0)=1, у(0)=2.

Решение. Имеем f(0)=1, f(0)=2.

Из данного уравнения находим ;

далее , ;

, ;

, .

…………………………………………………………

Подставляя найденные значения производных в ряд Маклорена, получаем приближенное решение

Если уравнение линейное, то удобнее искать коэффициенты разложения частного решения по методу неопределенных коэффициентов. Для этого подставляем ряд в дифференциальное уравнение и приравниваем коэффициенты, стоящие при одинаковых степенях х, в обеих частях уравнения.

Пример 10.13.5. Найти решение уравнения

,

удовлетворяющее начальным условиям у(0) = 0, у(0) = 1.

Решение. Решение ищем в виде степенного ряда

На основании начальных условий находим С₀ = 0, С₁ = 1.

Следовательно,

,

,

.

Приравниваем коэффициенты при одинаковых степенях х:

, откуда С₂=0,

, откуда С₃=1,

, откуда С₄=0,

…………………………………………………………..

, откуда .

………………………………………………………………….

Следовательно,

, , , …,

, … .

С₄=0, С₆=0, …, С_2n=0, … .

Подставляя найденные коэффициенты, получаем искомое решение

Полученный ряд сходится при всех значениях х.

Заметим, что найденное частное решение можно выразить через элементарные функции: вынося х за скобку, получим в скобках разложение в ряд функции . Следовательно, .