Решение обыкновенного дифференциального уравнения первого порядка методом Эйлера

Метод Эйлера - простейший метод решения задачи Коши, позволяющий интегрировать дифференциальное уравнение первого порядка. Его точность невелика, поэтому на практике им пользуются довольно редко, но на примере этого метода легче понять алгоритмы других, более эффективных методов.

Метод Эйлера основан на разложении функции в ряд Тейлора в -окрестности точки :

Если мало, то составляющие, содержащие во второй и более высоких степенях, являются малыми более высоких порядков малости и ими можно пренебречь. Тогда

(3)

где - значение правой части дифференциального уравнения (1) при подстановке в него начальных условий и Используя значение из разложения в -окрестности точки , получаем

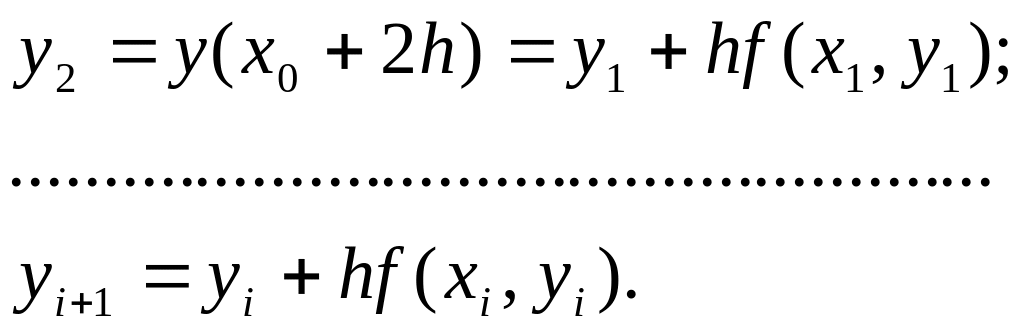(4)

При достаточно малой величине шага ( 0) метод Эйлера сходится на любом конечном отрезке. Его погрешность при погрешности на каждом шаге интегрирования Метод устойчив.

Геометрический смысл метода. Запишем уравнение касательной к интегральной кривой в точке : где - угловой коэффициент касательной, тогда

Подставив в уравнение , получим

или . (5)

Это соотношение определяет ординату точки , расположенной на касательной (рис.1). Выражения (3) и (5) одинаковы, следовательно, геометрический смысл метода Эйлера состоит в том, что в интервале дугу интегральной кривой заменяют отрезком касательной к ней, проведенной к этой кривой в точке Затем из точки проводят новый отрезок касательной уже к интегральной кривой, проходящей через точку Продолжая построение таких отрезков, получают ломаную Эйлера. Ломаная Эйлера проходит через заданную точку и приближает искомую интегральную кривую.

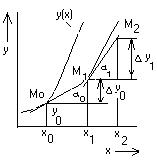
Рис.1. Схема метода Эйлера

Пример 1. Методом Эйлера найти решение уравнения при начальном условии на отрезке [0; 0,2] с шагом = 0,1. Точное решение уравнения .

Решение. Запишем расчетную формулу метода Эйлера:

Все вычисления удобно вести в виде таблицы 1.

Таблица 1. Табличный алгоритм метода Эйлера

0 1 2	0 0,1 0,2	1,0 1,1 1,19182	1,0 0,9182	0,1 0,09182	1,0 1,09545 1,18322

Абсолютная погрешность  = 1,19182 - 1,18322 = 0,0086; относительная погрешность  = 0,0086/1,18322 • 100 = 0,7 %.

Модифицированный метод Эйлера

В расчетных формулах метода Эйлера тангенс угла наклона касательной к истинной кривой не меняется на всем интервале длиной h . Так, на первом участке тангенс угла наклона известен и равен , т.е. производной в начальной точке . Но вдоль отрезка угол наклона касательной непрерывно изменяется.

Следовательно, оставляя неизменным угол наклона касательной на всем интервале , вносим погрешность в результат вычислений. Очевидно, точность метода Эйлера можно повысить, если учесть изменение производной по длине интервала , т.е. улучшить аппроксимацию производной. Эта идея заложена в модифицированном методе Эйлера (методе Эйлера-Коши), в котором в качестве производной принимается ее среднее значение на интервале . Чтобы получить значение производной в точке нужно иметь хотя бы приближенное значение функции в этой точке. Это значение можно получить по методу Эйлера, т.е.

(6)

где - искомое приближенное значение функции в конце интервала. По значению определяется приближенное значение производной в конце интервала Вычислив среднее значение полученных производных, находят уточненное значение функции :

(7)

Погрешность этого метода на каждом шаге интегрирования имеет порядок суммарная погрешность но затраты времени на получение решения увеличиваются.

С геометрической точки зрения в модифицированном методе Эйлера происходит замена дуги интегральной кривой в интервале отрезком прямой, проходящей через точку и угловой коэффициент которой равен среднему арифметическому значению угловых коэффициентов касательных к интегральным кривым в точках и

Пример 2. Решить дифференциальное уравнение примера 1 модифицированным методом Эйлера.

Решение. Расчет выполняем по формулам (6) и (7) в такой последовательности:

• определяем значение производной в начале интервала интегрирования;

• вычисляем приближенное значение функции в конце интервала по формуле (6);

• находим приближенное значение производной в конце интервала;

• определяем среднее значение производной на интервале :

• находим уточненное значение функции в конце интервала по формуле (7), т.е.

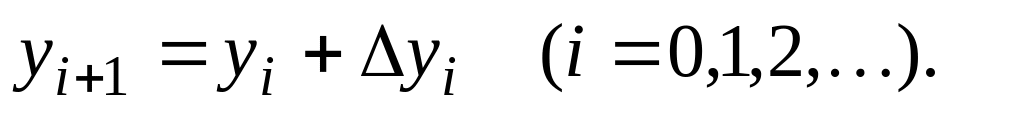
Все вычисления представим в таблице 2.

Таблица 2.Табличный алгоритм модифицированного

метода Эйлера

					Δ
0	0 0,1	1,0 1,1	1,0 0,9182	0,1 0,0918	0,0959	1,0
I	0,1 0,2	1,0959 1,1872	0,9134 0,8513	0,09134 0.08513	0,08824	1,09545
2	0,2	1,18414				1,18322

Примечание. Для каждого значения первая строка соответствует верхним формулам, вторая - нижним.

Абсолютная погрешность значений  =1,18414-1,18322= 0,00092, относительная - =0,08%, т.е. точность вычислений на порядок выше, чем при решении простым методом Эйлера.