Математическая модель
Ограничения на ресурсы станков:
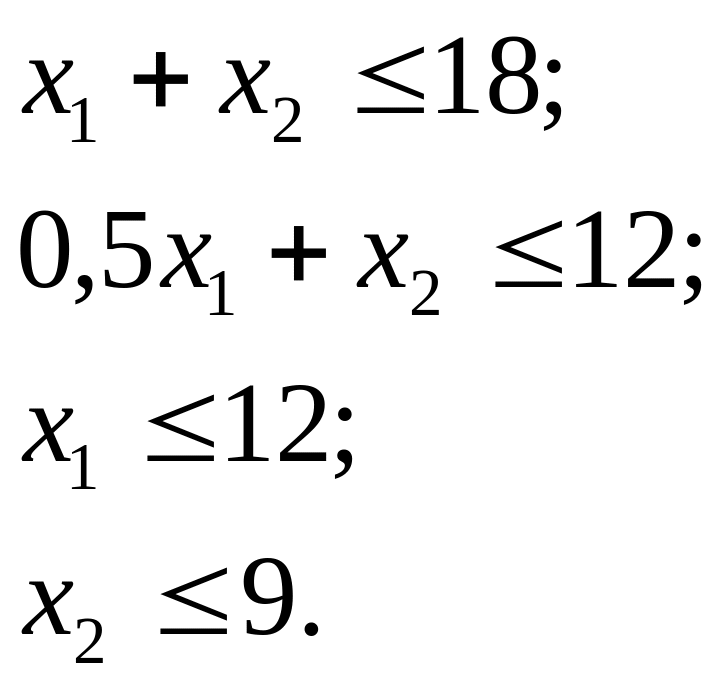
Граничные условия:
.Дополнительные ограничения: , - целые.
Целевая функция
max.
Графический метод решения задачи лп
Так как в задаче всего две переменных, то ее можно решить графически. Случай двух переменных не имеет особого практического значения, но он помогает дать геометрическое истолкование ограничений и поясняет смысл решаемой задачи. Задача решается в два этапа:
построение множества допустимых решений;
нахождение точки множества, координаты которой дают оптимальный план.
Определение множества допустимых решений, т.е. множества точек, координаты которых удовлетворяют системе ограничений и граничным условиям. Неравенства означают, что множество допустимых планов расположено в положительной полуплоскости (рис.1).
Рассмотрим первое ограничение, переписав его в виде равенства
Строим
прямую линию по двум точкам. Пусть
=
0, тогда
=
18. Если
=
0, то
= 18. Для
определения полуплоскости расположения
точек допустимого плана, нужно в
неравенство
подставить координаты произвольной
точки рассматриваемой полуплоскости,
например, точки с координатами
=1 и
= 1. Так как неравенство удовлетворяется
(1 + 1
18), то допустимые решения (точки) будут
расположены в полуплоскости ниже прямой,
характеризующей ресурс «токарный
станок». Отметим расположение определяемых
точек штриховкой прямой «токарный
станок». Изобразим графически остальные
ограничения. Из рис.1 видно, что если
будет выполняться ограничение по
фрезерному станку, то ограничение по
токарному станку несущественно и его
можно отбросить. Существенны ограничения
в виде многоугольника ОАВСД, т.е. этот
многоугольник определяет множество
допустимых планов, но какое из сочетаний
и
принесет предприятию максимальную
прибыль?
Оптимальными будут те точки множества допустимых планов, координаты которых обеспечат целевой функции наибольшее значение. Если оптимальный план единственный, то точка будет одна.
Определение оптимального плана. Строим линию уровня по уравнению целевой функции
=
,
где
– произвольное число (
).
Примем
= 1200, так как 1200 делится без остатка на
400 и 600. Тогда
Следовательно,
=3
и
=2.
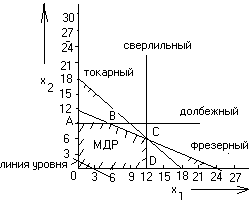
Рис. 1. Графическое решение задачи
При смещении линии уровня параллельно самой себе в направлении возрастания переменных и значение целевой функции растет и самое большое ее значение будет в точке С. В этой точке линия уровня еще касается многоугольника множества допустимых решений. Все точки на линии уровня определяют одну и ту же прибыль. На рис.1 точка С имеет координаты = 12 и = 6. Определим координаты точки С аналитически. В этой точке пересекаются две прямые линии, характеризующие существенные ограничения,
0,5 + = 12;
= 12 .
Следовательно,
.
Полученное решение является оптимальным
суточным производственным планом,
который принесет прибыль предприятию
в размере
Следовательно, . Полученное решение является оптимальным суточным производственным планом, который принесет прибыль предприятию в размере
При графическом методе решения задачи возможны следующие случаи:
оптимальный план единственный – линия уровня и множество допустимых решений имеют одну общую точку (рис. 2, а);
бесконечное множество оптимальных планов – предельное положение линии уровня совпало с границей множества допустимых решений (рис.2, б);
область допустимых решений не замкнута, т.е. целевая функция не ограничена сверху и может неограниченно возрастать – задача не имеет решения (рис.2, в);
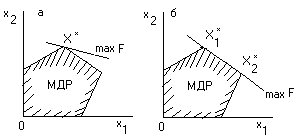
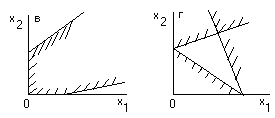
Рис.2. Графический метод решения задач ЛП
задача не имеет решения, так как область допустимых решений – пустое множество, т.е. система ограничений задачи несовместна (рис.2, г).