6.3. Решение уравнений состояния линейных стационарных сау. Вычисление фундаментальной матрицы

Рассмотрим методику решения уравнения состояния линейной стационарной системы, находящейся в свободном движении. При этом внешние воздействия на систему не действуют ( X_вх(t)= 0 ) и поведение системы описывается однородным векторным дифференциальным уравнением:

.                                                   (6.15)

Решение этого уравнения ищем в виде:

,                                                     (6.16)

где Ф(t)  –  фундаментальная матрица;   X(t₀)  –  вектор, описывающий состояние системы в начальный моментвремени t₀ .

Для стационарных линейных САУ решение матричного уравнения (6.15) можно получить по аналогии с решением скалярного дифференциального уравнения  в виде:

,                                                      (6.17)

где   –  матричная экспонента.

Из сравнения выражений (6.16) и (6.17) следует, что фундаментальная матрица равна: 

Ф(t) = exp(At).                                                       (6.18)

Существует несколько способов определения фундаментальной матрицы.

Первыйспособоснован на известном разложении экспоненты в ряд. Для выражения  (6.18) такое разложение принимает вид:

exp(At) = 1 + ,

где 1 – единичная матрица.

Указанный способ определения фундаментальной матрицы обычно используется при численных расчетах для фиксированного момента времени t = t₀.

При этом

exp(At₀) = 1 + At₀ + A² + A³ +…….

Вычисление подобного выражения для электронных вычисли­тельных машин является стандартной задачей, не представляющей каких-либо затруднений даже для систем высокого порядка.

Второй способвычисления фундаментальной матрицы предполагает использование аналитического выражения дляФ(t). Для его определения выполним преобразование Лапласа над обеими частями матричного дифференциального уравнения (6.15):

или ,

откуда

.                                              (6.19)

Матрица [р1–А] называетсяхарактеристической матрицей, ее определитель

det[p1-A] = 0

представляет собой характеристическое уравнение САУ в матричной форме.

Умножая обе части уравнения (6.19) слева на матрицу    [р1–А]^-1,    обратную    по   отношению к [р1–А], получим:

X(p) =  [р1–А]^-1 X(0).

Выполнив обратное преобразование Лапласа над последним уравнением, имеем

X(t) =L^-1{[р1–А]^-1} X(0).

Из последнего выражения следует, что фундаментальная матрица равна:

(6.20)

В качестве примера определим фундаментальную матрицу системы, передаточная функция которой равна:

.                                                (6.21)

Преобразуем  выражение (6.21)  к  виду:

.                             (6.22)

Используя метод прямого программирования, составляем для рассматриваемой системы схему   переменных состояния (рис. 6.7), в качестве которых выбираем выходной сигнал системы и его первую производную, т.е. , а .

Система дифференциальных уравнений для переменных состояния:

Кроме того, .

Соответствующие приведенной системе дифференциальных уравнений векторные уравнения имеют вид:

=;

.

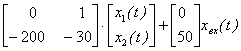Таким образом, матрицы системы, управления и наблюдения принимают вид:

A;               B ;                  C .

Характеристическая матрица равна:

.

Матрица, обратная характеристической, равна:

.

В соответствии с выражением (6.20) фундаментальная матрица равна:

=