9. Затухающие колебания

   1. Дифференциальное уравнение затухающих колебаний, его решение

Затухающие колебания происходят в замкнутой механической системе (=0), в которой имеются потери энергии на преодоление сил сопротивления (β ≠ 0) или в закрытом колебательном контуре (U_внеш=0), в котором наличие сопротивления R приводит к потерям энергии колебаний на нагревание проводников (β ≠ 0).

В этом случае общее дифференциальное уравнение колебаний (5.1) примет вид

. (5.44)

Решением уравнения (5.44) являются затухающие колебания

, (5.45)

где амплитуда колебаний убывает со временем по экспоненциальному закону

(5.46)

а циклическая частота затухающих колебаний определяется формулой

, (5.47)

из которой следует, что .

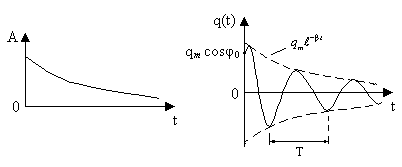Графики зависимости от времени t амплитуды и заряда на обкладках конденсатора приведены на рис. 5.15.

Рис. 5.15

В случае механической системы по табл. аналогий 5.1 можно получить уравнения, подобные уравнениям (5.44), (5.45):

, (5.48)

. (5.49)

Отметим только, что для получения затухающих колебаний вида (5.49) необходимо, чтобы сила сопротивления, действующая в механической системе, была пропорциональна скорости движения тела

. (5.50)

Только в этом случае получается дифференциальное уравнение затухающих колебаний в виде (5.48). Формула (5.50) справедлива для небольших числовых значений скоростей движения тела (м.т.).

В заключение этого параграфа отметим, что из-за уменьшения с течением времени амплитуды колебаний затухающие колебания не являются периодическими. Но при малом затухании под периодом (его также называют условным периодом) можно понимать минимальное время, за которое повторяются минимальные значения или максимальные значения величин, описывающих колебательное движение (см. рис. 5.15). Аналогично циклическую частоту затухающих колебаний называют условной циклической частотой.

2. Характеристики, вводимые для описания затухающих колебаний

Рассмотрим кратко величины, вводимые для описания затухающих колебаний.

1.Критическое сопротивление контура (критический коэффициент сопротивления среды ). Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинаетсяапериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя один раз положение равновесия, заряд конденсатора в итоге монотонно будет убывать до нуля (кривая 2 на рис. 5.16).

Рис. 5.16

Убывание заряда , смещениятела в механической системе по кривым 1 или 2, либо по кривой, расположенной между ними, зависит от начальных условий. Например, если поместить физический маятник в жидкую вязкую среду и, отклонив его от положения равновесия, отпустить без начальной скорости, то тогда смещениемаятника будет изменяться по кривой 1 (рис. 5.16,б). Если же отпустить маятник с начальной скоростью, направленной к положению равновесия, то тогда его смещение может со временем изменяться по кривой 2 (рис. 5.16,б), т.е. он пройдет один раз положение равновесия, затем отклонится, и после этого в итоге будет монотонно приближаться к положению равновесия.

Выведем формулу для критического сопротивления контура через параметры контураL и C. При увеличении сопротивления угловая частота затухающих колебаний будет уменьшаться, а период колебаний Т_З будет возрастать, и для сопротивления , равного, можно записать

: ,,

. (5.51)

Для в контуре наблюдается апериодический разряд, а при в контуре происходят затухающие колебания.

По таблице аналогий (см. табл. 5.1) для критического коэффициента сопротивления среды можно записать (L® m, 1/С ® к)

. (5.52)

2. Время релаксации τ – это время, в течение которого амплитуда колебаний убывает в e раз (e-основание натурального логарифма):

, . (5.53)

За время релаксации в системе совершается N_e полных колебаний:

(5.54)

3. Логарифмический декремент затухания δ равен натуральному логарифму отношения двух амплитуд, взятых через период:

. (5.55)

4. Добротность Q системы можно ввести как величину, определяющую потери энергии колебаний системы за один условный период колебаний,

. (5.56)

Полная энергия колебаний пропорциональна квадрату амплитуды колебаний и поэтому выражение (5.56) можно записать в следующем виде:

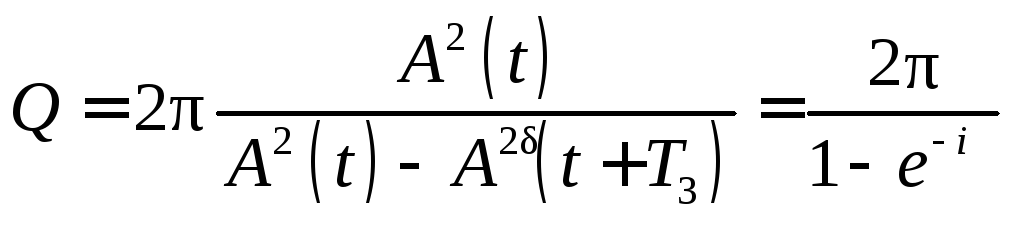. (5.57)

Из формулы (5.56) следует, что чем выше добротность Q системы, тем медленнее в ней затухают колебания.

Приведем ориентировочные значения Q для различных систем:

1) колебательный контур на радиочастотах ( ~ 10⁶ рад/с): Q ~ 100; 2) полый резонатор диапазона сверхвысоких частот (ω ~ 10¹¹ рад/с): Q ~ 10⁵; 3) камертон: Q ~ 10⁴; 4) колебания кварцевой пластины: Q ~ 10⁵; 5) излучение атома как колебательной системы: Q ~ 10⁷.

Как видно, для применяемых на практике систем Q ³ 100, т.е. для них выполняются условия малого затухания:

.

Тогда из формулы (5.57) получим ()

. (5.58)

Для добротности механической системы и колебательного контура из формулы (5.58) в условиях малого затухания можно получить следующие формулы:

, . (5.59)