3. Общие дифференциальные уравнения, описывающие колебания в произвольной системе

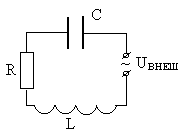Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение и имеются потери энергии на нагревание проводников (рис. 5.3).

Из закона сохранения энергии следует, что элементарная работатока, поступающего в контур извне, расходуется на изменение энергии колебаний и на нагревание проводников :

Рис. 5.3

.

Распишем это выражение

,

, ,

,

,

, (5.1)

где введены следующие обозначения:

, (5.2)

. (5.3)

Буквой β в формуле (5.2) обозначен коэффициент затухания колебаний, а величина в формуле (5.3) называетсяциклической (круговой) частотой свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β=0).

Уравнение (5.1) описывает различные случаи колебаний в открытом и закрытом колебательных контурах. Для получения аналогичного уравнения, описывающего колебания в механической системе, воспользуемся табл. аналогий 5.1:

, (5.4)

, , (5.5)

где – проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.

Рассмотрим частные случаи решения уравнений (5.1) и (5.4).

4. Механические незатухающие гармонические колебания в замкнутой системе

Для замкнутой системы (=0), в которой отсутствуют потери энергии на преодоление сил сопротивления или трения (β=0), дифференциальное уравнение (5.4) примет вид

. (5.6)

Из теории дифференциальных уравнений следует, что решением этого уравнения (его называют однородным линейным дифференциальным уравнением второго порядка) является гармоническое колебание

, (5.7)

т.е. смещение х тела (материальной точки) от положения равновесия изменяется по гармоническому закону. В уравнении (5.7) введены такие понятия, как

х_m – максимальное смещение или амплитуда колебания. В общем случае под амплитудой колебаний понимают положительную величину, стоящую перед знаком синуса или косинуса;

-–фаза колебаний – величина, стоящая под знаком синуса или косинуса;

–начальная фаза колебаний – фаза колебаний в начальный момент времени t=0;

–циклическая (круговая) частота свободных незатухающих гармонических колебаний системы, определяемая свойствами системы по формуле (5.5).

Циклическая частота связана спериодом колебаний Т и линейной частотой ν соотношениями

. (5.8)

Запишем выражения для проекций скорости, проекции ускорения тела (м.т.) на ось Ох, потенциальной, кинетической и полной энергий тела, совершающего гармонические колебания

, ; (5.9)

, ,; (5.10)

, ; (5.11)

, . (5.12)

Покажем, что амплитуды колебаний кинетической и потенциальной энергий совпадают

.

Тогда

. (5.13)

Итак, из полученных формул следует, что проекция скорости и ускорения, кинетическая и потенциальная энергииW_K, W_P тела (м.т.) изменяются по гармоническому закону подобно ее смещению х, а полная энергия W колебаний м.т. остается при этом неизменной.

Приведем в пределах одного периода Т колебаний графики зависимости х, ,,W_K, W_P и W от времени t для м.т. при ее гармонических колебаниях (рис. 5.4, начальная фаза колебаний считается равной нулю:). При построении графиков удобно записать уравнения колебаний в видеи выбирать моменты времени, равные Þ.

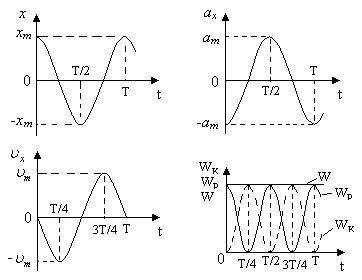
Рис. 5.4

Отметим, что для потенциальной и кинетической энергий период гармонических колебаний оказывается в два раза меньше, чем для смещения х.