
- •Омский государственный технический университет
- •Список сокращений и обозначений
- •Краткая история развития теории эмп
- •1. Основные понятия теории электромагнитного поля
- •2. Описание свойств векторных полей
- •2.2. Дифференциальные характеристики физических полей
- •Если в какой-либо точке , то в этой точке находится«исток» поля(рис. 2.5). Там, где, – соответственно«сток». На рис. 2.5. Приведена система положительного и отрицательного сосредоточенных зарядов.
- •2.3.Основные теоремы векторного анализа
- •Теорема м. Остроградского – к. Гаусса Данная теорема расширяет понятие дивергенции для конечного объема.
- •Теорема д. Стокса
- •2.4. Оператор набла и оператор п. Лапласа
- •Некоторые тождества и операции второго порядка.
- •2.5. Классификация векторных полей
- •3. Система уравнений Максвелла
- •3.1. Уравнения Максвелла в интегральной форме
- •3.2. Уравнения Максвелла в дифференциальной форме
- •3.3. Уравнение непрерывности
- •3.4. Уравнения Максвелла в комплексной форме
- •3.5. Тангенс угла диэлектрических потерь. Классификация сред
- •4. Граничные условия для векторов эмп
- •4.1. Нормальные составляющие
- •4.2. Тангециальные составляющие
- •5. Теорема Умова-Пойтинга. Баланс эм энергии.
- •6. Волновые уравнения для векторов эмп.
- •7. Решение волновых уравнений. Плоские волны
- •7.1. Плоские эмв как частные решения волновых уравнений
- •7.2. Коэффициенты затухания и фазы
- •7.3. Параметры эмв
- •8. Плоские эмв в диэлектриках
- •8.1. Параметры эмв в диэлектриках с потерями
- •8.2. Поведение диэлектриков в эмп
- •8.3. Поглощение эмп веществом. Диэлектрический нагрев
- •9. Эмп в проводниках. Скин-эффект
- •9.1. Сопротивление проводников на высоких частотах
- •9.2. Сопротивление цилиндрического проводника (общий случай)
- •9.3. Граничные условия на границе идеального проводника
- •10. Эмв в реальных средах
- •10.1. Общая схема анализа эмв в реальных средах
- •10.2. Поляризация эмв
- •10.3. Классификация эмв
- •11. Скалярный и векторный потенциалы эмп
- •11.1. Волновые уравнения для электродинамических потенциалов. Условия калибровки Лоренца и Кулона
- •11.2. Электродинамические потенциалы в безграничном пространстве
- •12. Классификация эмп
- •12.1. Электростатическое и магнитостатическое поля
- •12.2. Стационарное и квазистационарное эмп
- •12.3. Эмп для весьма высоких частот
- •13. Эмв на границе раздела сред
- •13.1. Наклонное падение эмв. Законы Снеллиуса
- •13.2. Коэффициенты отражения и преломления.
- •13.3. Формулы Френеля
- •13.4. Явление полного отражения
- •13.5. Явление полного прохождения
- •13.6. Стоячая волна. Ксв. Кбв
- •14. Связь между продольными и поперечными составляющими эмп
- •Аналогично получается для магнитной составляющей:
- •15. Телеграфные уравнения. Волновые уравнения для напряжения и тока
- •Приложение 1. Некоторые понятия векторной алгебры
- •Приложение 2. Криволинейные системы координат
- •Операции векторного анализа в цск и сск.
- •Приложение 3. Эм параметры некоторых веществ Параметры диэлектриков (при 20с) [5, 19]
- •Параметры проводников
- •Параметры магнитномягких материалов [5]
- •Приложение 4. Некоторые сведения о волновых уравнениях
- •Приложение 5. Некоторые сведения о функциях Бесселя
- •Список литературы
- •Оглавление
- •1. Основные понятия теории электромагнитного поля . . . . . . . . . . . . . . .
- •Приложение 5. Некоторые сведения о функциях Бесселя . . . . . . . . . .
2. Описание свойств векторных полей
Математический аппарат, применяемый для описания свойств векторных полей, называется векторным анализом. Наибольшую наглядность понятия и величины векторного анализа имеют в случае поля вектора скорости текущей несжимаемой жидкости[3, 8, 9]. В дальнейшем будут рассматриваться примеры и аналогии именно из этой области.
2.1. Интегральные характеристики физических полей
Важные характеристики векторного поля – циркуляцияипоток.
Циркуляцией(Ц) векторного поля![]() по замкнутому контуруLназывается число, равное значению
криволинейного интеграла второго рода
по замкнутому контуруLназывается число, равное значению
криволинейного интеграла второго рода![]() .
.
В случае текущей жидкости предполагается,
что во всем объеме, кроме канала,
образованного контуромL(рис. 2.1), жидкость мгновенно замораживается.
В зависимости от характера поля жидкость
в канале окажется либо неподвижной,
либо будетциркулировать(двигаться вдоль контура)[8]. В данном
случае мера циркуляции – произведение
скорости жидкости в канале на длину
контура. После преобразований[8]приходим к формуле (2.1).
случае текущей жидкости предполагается,
что во всем объеме, кроме канала,
образованного контуромL(рис. 2.1), жидкость мгновенно замораживается.
В зависимости от характера поля жидкость
в канале окажется либо неподвижной,
либо будетциркулировать(двигаться вдоль контура)[8]. В данном
случае мера циркуляции – произведение
скорости жидкости в канале на длину
контура. После преобразований[8]приходим к формуле (2.1).
Ц
=
![]() =
=![]() .
(2.1)
.
(2.1)
Д ля
силового поля циркуляция – это работа
силы по контуруL.
ля
силового поля циркуляция – это работа
силы по контуруL.
Потоком
(Фп) векторного поля
![]() через поверхностьS
(рис. 2.2) называется число, равное значению
поверхностного интеграла второго рода
через поверхностьS
(рис. 2.2) называется число, равное значению
поверхностного интеграла второго рода
![]() .
.
В
случае текущей жидкости ее потоком
через поверхность S
будет объем жидкости, протекающей в
единицу времени через эту поверхность.
Элементарный поток через dS
(рис. 2.2) за единицу времени будет равен
скалярному произведению вектора поля
на вектор dS![]() .
После преобразований [8]
получим:
.
После преобразований [8]
получим:
Фп
=
![]() =
=![]() . (2.2)
. (2.2)
Знак потока зависит от выбора направления нормали к dS. В случае замкнутых поверхностей принято вычислять поток, «вытекающий» наружу, поэтому выбирается внешняя нормаль [8].
Для анализа векторного поля в конкретной точке пространства необходимо перейти к дифференциальным характеристикам.
2.2. Дифференциальные характеристики физических полей
В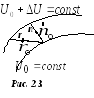 векторном анализе удобно использовать
дифференциальные операторыградиент,
дивергенцию,
ротор.
векторном анализе удобно использовать
дифференциальные операторыградиент,
дивергенцию,
ротор.
Градиент
– векторная
характеристика скалярного
поля. Градиентом
скалярной
функции
называется вектор,
численно равный производной от этой
функции по направлению нормали к
поверхности уровня и направленный по
этой нормали:
![]() .
Градиент численно равен максимальной
скорости изменения функции (на рис. 2.3
.
Градиент численно равен максимальной
скорости изменения функции (на рис. 2.3![]() ,
поскольку
,
поскольку![]() ).
Направление градиента совпадает с
направлением быстрейшего изменения
функции (
).
Направление градиента совпадает с
направлением быстрейшего изменения
функции ( ).
).
В декартовой системе координат
 =
=![]() . (2.3)
. (2.3)
Таким образом, градиент представляет собой скорость пространственного изменения скалярной величины, - каждая его компонента показывает скорость изменения вектора по соответствующей координате. Градиент ориентирован в таком направлении, где он имеет самую длинную проекцию [3].
Д ивергенция
– это скалярная
характеристика векторного
поля.
ивергенция
– это скалярная
характеристика векторного
поля.
Дивергенция
векторного
поля
![]() -
этоскалярная
величина,
равная пределу отношения потока
через замкнутую
поверхность S
к объему,
заключенному внутри этой поверхности
(рис. 2.4), при условии, что поверхность
стягивается в точку.
-
этоскалярная
величина,
равная пределу отношения потока
через замкнутую
поверхность S
к объему,
заключенному внутри этой поверхности
(рис. 2.4), при условии, что поверхность
стягивается в точку.
 .
(2.4)
.
(2.4)
Дивергенция характеризует интенсивностьисточников поля. Если![]() ,
это значит, что в данной точке нет
источников.
,
это значит, что в данной точке нет
источников.
В декартовой системе координат
![]()
 . (2.5)
. (2.5)
Данная формула выводится путем анализа потока через поверхность, охватывающую объем V(рис. 2.4). Анализируя потоки внутрь и наружу для составляющейFy , получаем:
![]() .
(2.6)
.
(2.6)
Аналогичные результаты получаются для FxиFz, что дает в результате
![]() .
(2.7)
.
(2.7)
После подстановки (2.7) в (2.4) получается (2.5) [3, 8].
